Sağlık Alanında İstatistik Dersi 5. Ünite Özet

Giriş

Değişkenler arasındaki ilişkinin derecesinin tespiti işlemine korelasyon analizi adı verilir. İki ya da daha fazla değişken arasındaki ilişkinin genel doğasının tanımlanmasına ise regresyon analizi adı verilir.

Regresyon analizi çalışmalarında iki farklı değişken tanımlamasına ihtiyaç duyulmaktadır. Bunlar sırasıyla bağımlı ve bağımsız değişken kavramlarıdır. Bağımlı değişken araştırmacının üzerinde çalıştığı değişken olup bu değişken üzerinde meydana gelen değişimler ya da bu değişkenin toplam değişkenliğinin açıklanmasına çalışılmaktadır. Bağımsız değişken ya da değişkenler ise ilgilenilen bağımlı değişkende meydana gelen değişim ya da toplam değişkenliğinin üzerinde etkisi olabileceği düşünülen değişken ya da değişkenlerdir.

Korelasyon Analizi

İki ya da daha fazla ve en az aralıklı ölçeğe uygun şekilde ölçümlenmiş değişkenler arasındaki ilişkinin derecesini belirlemek için Pearson korelasyon katsayısı kullanılır. Bu katsayı r ile gösterilir. Pearson r korelasyon katsayısı -1 ile +1 arasında değişen değerler almaktadır. -1 ve +1 değerlerine eşit sonuçlar, değişkenler arasında mükemmel/tam ilişkinin varlığını gösterir. Değerin sıfıra bu kadar yaklaşmasından dolayı bu iki değişken arasında “korelasyon yoktur” denilmesi doğru olacaktır.

Korelasyon katsayısı yardımıyla değişkenler arasındaki ilişki ifade edilirken zayıf, orta ilişki gibi nitelemelerin gerçekleştirilmesi söz konusudur. Araştırmacılar, herhangi bir değişkende meydana gelen değişimin, bu değişkenle ilişkili olduğunu düşündükleri değişken tarafından ne kadarının açıklandığını tespit etmeleri gerektiğinde belirlilik katsayısı hesaplanır.

Çoğunlukla araştırmalarda örneklemler ile çalışılmaktadır. Bir araştırmada örneklem sonuçlarına göre belirlenen korelasyon değerinin ana kütle içinde geçerli olup olmadığının belirlenmesi için test edilmesi istenebilir. Örneklem sonuçlarına göre “korelasyon yoktur” kararı verildiyse bu kararın ana kütle için de geçerli olup olmadığı testi Pearson korelasyon katsayısı anlamlılık testi yardımıyla yapılır.

Basit Doğrusal Regresyon Analizi

Korelasyon katsayısı yardımıyla iki değişken arasındaki doğrusal ilişkinin derecesi tespit edilebilmektedir. İki değişken arasında bir ilişkinin varlığının gösterilmesi ile beraber ilgili değişkenler arasında matematiksel bir model kurulması istenebilir. Araştırmacının ilgilendiği bağımlı değişken y, bağımsız değişken x iken y’nin değerlerinin tahmini için x’in değerleri kullanılabilir. Doğrusal ilişki için gerekli eşitliğin hesaplanması ve tahminlerin oluşturulması işlemi regresyon analizi olarak adlandırılır. Bir bağımlı bir de bağımsız değişkenin olduğu durumlarda basit doğrusal regresyon analizi adını alır. İki değişken arasındaki doğrusal ilişkinin gösteriminde kullanılan eşitliğe regresyon denklemi adı verilir. Değişkenler arasındaki ilişkiler doğrusal olabileceği gibi eğrisel ya da kübik formda da olabilir. Bu ünite çerçevesinde değişkenler arasındaki ilişkilerin doğrusal olduğu varsayılmaktadır. Doğrusal regresyon denkleminin tahmini için bir çok teknik kullanılabilmekle birlikte en çok kullanılan teknik en küçük kareler tekniği bu ünite içerisinde ele alınmaktadır. n adet gözleme sahip bir veri setinde x bağımsız değişken y’de bağımlı değişken olmak üzere gözlem birimleri için ölçüm sonuçları yer alabilir. x ve y değişkenleri arasındaki olası bir ilişki izleyen doğrusal model yardımıyla araştırılabilir. Basit doğrusal regresyon modeli,

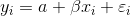
En küçük kareler tekniği yardımıyla ? ve ß parametrelerinin tahminleri a ve b’nin hesaplanması için,

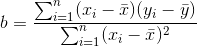
ve

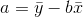
eşitlikleri kullanılır. Parametre tahminleri yardımıyla basit doğrusal regresyon denklemi,

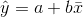
olarak yazılır. Araştırmada ilgilenilen x ve y değişkenlerinin standart sapmalarının bilinmesi durumunda b için;

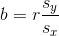
eşitliği de kullanılabilir. Parametre değerleri belirlendikten sonra x ve y değişkenleri için regresyon doğrusu saçılım grafiğinde gösterilir. Regresyon denklemi yardımıyla araştırmacı gözlemlediği herhangi bir x değeri için y’nin alacağı değeri tahmin edebilir. Denklemde x yerine ilgilendiği değeri yazan araştırmacı y’nin modele göre beklenen değerini hesaplamış olur. Benzer şekilde y’nin bir değeri için x’in modele göre beklenen değeri de hesaplanabilir. Yapılan hesaplamaların doğru ve uygun olması için regresyon analizinde uyulması gereken 5 adet varsayım bulunmaktadır. Bu varsayımlar;

1. ? rassal değişkeni x’in değerlerinden istatistiksel olarak bağımsızdır,
2. ? rassal değişkeni Normal dağılıma sahiptir,
3. ? _i rassal değişkeni 0 aritmetik ortalamaya sahiptir,
4. ? _i ve ? _j gibi birbirinden farklı iki hata istatistiksel olarak bağımsız olmalıdır,
5. ? _i rassal değişkenleri x _i’ lerin tüm değerleri için sabit bir varyansa sahiptir, olarak sıralanırlar.

Tahminin standart hatası kavramını inceleyebilmek için öncelikle regresyon analizinde ele alınan toplam değişkenliğin bileşenlerini incelemekte fayda vardır. Regresyon analizinde ile y değişkeninin ortalaması ( 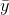) arasındaki fark toplam değişim olarak adlandırılır. Bu toplam değişim iki ana bileşene kolaylıkla ayrılabilir. Bu bileşenler açıklanabilen değişim ve açıklanamayan değişim bileşenleri olarak adlandırılırlar. Açıklanamayan değişim gözlem birimlerinin gözlemlenen değerleri ile modele göre tahmin edilen değerleri arasındaki fark ( 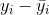) olarak ifade edilirken, açıklanabilen değişim gözlem birimlerinin gözlemlenen değerleri ile bağımlı değişken y’nin ortalaması arasındaki fark ( 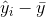) olarak ifade edilir. Açıklanamayan değişim i’inci gözlemin hata terimi olarak adlandırılırken, açıklanan değişim i’inci gözlemin regresyon denklemi tarafından açıklanan kısmını temsil edecektir. Genel bir ifade ile toplam değişim için,

Toplam D. = Açıklanamayan D. + Açıklanan D.

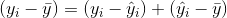
eşitliği yazılabilir.

İlgilenilen iki değişken arasındaki doğrusal ilişki için, en küçük kareler tekniği kullanılarak, bir regresyon doğru denklemi tahmini işlemlerini buraya kadar yürüttükten sonra dikkatin “yi değerlerini tahmin ederken x bağımsız değişkeninin değerlerini bilmenin gerçekten faydası var mıdır?” sorusunun cevabının araştırılmasına verilmesi gerekmektedir. Örneğin doğrunun eğimini veren ß katsayısı 0’a eşit ise ya da istatistiksel olarak test edilerek 0’a eşit olarak bulunur ise modelden parametrenin çıkartılması gerekecektir. Dolayısıyla da x değişkenine ihtiyaç kalmayacaktır. Bu durumda ana kütle regresyon doğrusu 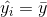olacak şekilde düz bir doğru olacaktır. Eğer ß değeri 0’a eşit değilse y’nin değerlerinin tahmininde x değişkeni kullanılabilecektir. Bundan dolayı y’nin değerlerinin tahmininde regresyon doğrusu kullanımının faydası olup olmadığını görmek için ß =0, sıfır hipotezinin test edilmesi gerekir. Alternatif hipotez ise ß’nın 0’dan büyük ya da küçük olmasına göre kurulabileceği gibi genellikle ß ? 0 olacak şekilde çift yönlü olarak kurulur.

İlgili hipotezler,

H ₀ : ß = ß ₀

H ₁ : ß ? ß ₀

şeklinde yazılırlar. Testin yürütülmesinde t testi kullanılır. ß’nın 0’a eşitliğinin test edilmesinde kullanılabilecek bir başka teknik de varyans analizi tablosu kullanımıdır. Bu tekniğin en büyük faydası birden fazla bağımsız değişken olması durumuna kolaylıkla genellenebilmesidir.

ß’nın 0’a eşit olup olmadığının test edilmesine ek olarak ß için güven aralığı da tespit edilebilir. Regresyon katsayısı b için n - 2 serbestlik derecesi ve sb standart sapması ile t dağılımı uyumu bilindiğine göre ana kütle regresyon doğrusu eğimi ß’nın güven aralığı,

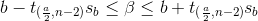
yardımıyla hesaplanır.

Kurulan regresyon modelinin bağımlı değişkenin ne kadarlık bir kısmını açıkladığını belirlemek amacı ile belirlilik katsayısı (R2 ) hesaplanabilir. Bu durumda belirlilik katsayısı varyans analizi tablosu yardımıyla,

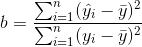
eşitliğiyle hesaplanır. Toplam değişimin açıklanamayan kısmı ise belirsizlik katsayısı olarak adlandırılır ve 1 - R ² ile hesaplanır.

Çoklu Doğrusal Regresyon Analizi

Bağımlı değişkenin daha iyi tahmin edilmesi ya da açıklanabilmesi için birden daha fazla bağımsız değişken tanımlanabilir. Bir bağımlı ve birden daha fazla bağımsız değişkenin bulunduğu regresyon analizi problemlerine çoklu regresyon analizi adı verilir.

n adet gözleme sahip bir veri setinde y bağımlı değişken ve k adet bağımsız değişken olmak üzere gözlem birimleri için ölçüm sonuçları yer alabilir (s 124, Tablo 4.8). Veri dizininin her bir satırı bir gözlem değerine karşılık gelmektedir. Eğer yürütülen araştırmada x’ler ile y değişkeni arasında doğrusal bir ilişki araştırılıyor ise çoklu doğrusal regresyon modeli,

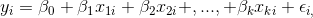
(i = 1, 2, ... , n; n ? k + 1) eşitliği yardımıyla tanımlanır. Model dikkatlice incelenirse ß0 katsayısının basit doğrusal regresyon modelinde ? ile gösterildiği görülebilir. Çoklu doğrusal regresyon modelinde doğrusallık özelliği parametrelerden gelmektedir. Araştırmacı isterse farklı parametreler için aynı değişkenin farklı kuvvetleri (kendisi, karesi, v.b.) ile de işlem yapabilir. Çoklu doğrusal regresyon modelinde yer alan parametrelerin tahminleri için basit doğrusal regresyon analizinde olduğu gibi en küçük kareler tekniği kullanılabilir. En küçük kareler tekniğine göre parametre tahminlerini bulmak için modelin öncelikle matris gösteriminde sunulması gerekir. Matris gösteriminde çoklu doğrusal regresyon modeli,

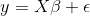
olacaktır. Regresyon katsayıları vektörü ß’nın en küçük kareler tahmincisi b ,

b = (X'X) ^-1 X'Y

matris işlemi ile hesaplanır. Basit doğrusal regresyon analizinde olduğu gibi çoklu doğrusal regresyon analizinde de ß’nın anlamlılık testi yürütülür. Burada dikkat edilmesi gereken nokta, çoklu doğrusal regresyon modelinde ß vektörü için işlem yapılmaktadır. Modelde yer alan tüm terimlerin tek tek anlamlılık testleri yürütülür ve anlamlı bulunmayan katsayılara ait değişkenler analizden çıkartılarak yeni bir model oluşturulur. Yine basit doğrusal regresyon analizinde olduğu gibi modelin anlamlılığını test etmek amacı ile varyans analizi tablosu oluşturulur. Daha sonra varyans analizi tablosu kullanılarak modelin belirlilik katsayısı da hesaplanır.