Tıbbi İstatistik Dersi 6. Ünite Özet

Giriş

Örnekleme, ana kütlenin birim sayısı bakımından daha az fakat araştırmaya konu olan özellikleri bakımından ana kütlenin temsili olan örneklemin oluşturulması ve örneklemden yararlanarak ana kütle parametrelerine ait tahminde bulunma faaliyetidir.

Tam Sayım ve Örnekleme

İstatistiksel araştırmaların amacı tanımlanan ve hakkında araştırma yapılacak birimler topluluğu olan ana kütlenin özellikleriyle ilgili bilgiler üretmektir.Bunun için iki yol vardır. Bunlar tam sayım ve örneklemedir.

Tam sayım

Tanımlanan ana kütlenin bütün birimleri üzerinden araştırmaya konu olan değişkenler itibariyle ilgiler üretmektir.

Örnekleme

Tanımlanan ana kütleden onu ilgilendiren değişkenler bakımından temsil eden sınırlı sayıda birimin belirli yöntemler kullanılarak seçilmesi ile ana kütle için tahmine dayalı bilgi edinme işlemine denir.

Örnekleme Yapmayı Gerekli Kılan Nedenler

Tanımlanan ana kütle sonsuz ana kütle olması durumunda tam sayım mümkün olmaz ve ya sonlu bir ana kütle olması durumunda ise,

• Zaman
• Maliyet
• Doğru veri elde etme
• İncelenecek birimlerin fiziksel zarara uğramaması
• Ana kütleyi oluşturan birimlerin değişkenliği

nedenlerinden dolayı örnekleme uygulamasına başvurmak kaçınılmazdır.

Örneklem için Birim Seçme Yöntemleri

Örnekleme girecek birimler için keyfi seçim ve tesadüfi seçim yöntemleri vardır.

Keyfi seçim

Bu yöntemde araştırmacı, hangi birimlerin örnekleme seçileceğini bilerek ve isteyerek belirler.

Tesadüfi seçim

Sonlu ana kütlelerde tesadüfi örneklem seçimi

Kura seçimi ve sistematik seçim olarak ikiye ayrılır.

Kura seçimi

Ana kütledeki tüm birimler numaralandırılarak bir torba ve ya bir kap gibi bir şeyin içine atılır.İçinden bir tane seçilir, seçilen torbaya ve ya kaba iade edildikten sonra tekrar seçme işlemi yapılır.Bu işlem n kez tekrarlanır.

Böylelikle herkese eşi seçilme şansı verilir ve her birimin seçilme olasılığı da eşit olmuş olur.

Sistematik seçim

Tüm birimler birden N e kadar numaralandırılır. Örneklem hacmi belirlenir. k=N/n oranı belirlenir.1,2,…., k adet sayı arasından tesadüfi bir tane seçilir. Çekilen sayı a ile gösterilsin. a, örnekleme girecek birinci birimdir. Bir sonraki birim a+k. terim olur. Her seferinde seçilen birimden k birim sonrası tekrar seçilir. Bu şekilde n hacimli örneklem oluşturulur.

Örnekleme Sürecinin Aşamaları

Ana kütlenin tanımlanması

• Çerçevenin belirlenmesi
• Örnekleme yönteminin seçilmesi
• Örneklem hacminin belirlenmesi
• Örneklemin uygulanması

Ana kütlenin tanımlanması

Araştırmacı tarafından belirlenen bir tanıma uyan ve hakkında bilgilerin üretileceği, çıkarımların yapılacağı birimlerden oluşan topluluktur.

Çerçevenin belirlenmesi

Sonlu bir ana kütlenin bütün birimlerinin kayıtlı olduğu bir listedir.

Örnekleme yönteminin seçimi

Örneklemeye girecek birimlerin belirlenmesine imkan veren yöntemlere denir.

Örnekleme Hacminin belirlenmesi

Örnekleme girecek birimlerin sayısını verir.

Örneklem Hacminin Belirlenmesine Etki Eden Faktörler

• Ana kütlenin homojenliği
• Araştırmada verilecek kararın önemi
• Araştırmanın yapısı

Örneklemin seçimi

Örnekleme girecek birimler keyfi veya tesadüfi seçim uygulamalarıyla seçilirler.

Örnekleme Yöntemleri

İki tür örnekleme yöntemi vardır.

1. Olasılıklı Olmayan örnekleme Yöntemleri
   • Kolayda örnekleme
   • Yargısal örnekleme
   • Kota örneklemesi
   • Kartopu örneklemesi
2. Olasılıklı örnekleme Yöntemleri
   • Basit tesadüfi örnekleme
   • Tabakalı örnekleme
   • Sistematik örnekleme
   • Tek ve çok aşamalı örnekleme

Olasılıklı olmayan örnekleme yöntemleri

Araştırmayı yapan kişi veya grubun istekleri ve değer yargıları örnekleme seçilecek birimlerin ve örneklem hacminin belirlenmesinde etkili oluyorsa yapılan örnekleme olasılıklı olmayan örneklemedir.

Kolayda örnekleme

Araştırma konusu ile ilgili kolay ulaşılabilir olan birimlerden bir örneklemin oluşmasıdır.

Yargısal örnekleme

Araştırmacının ya da örneklemecinin kişisel arzu, düşünce ve deneyimlerine göre seçmiş olduğu örneklemedir.

Kota örneklemesi

Ana kütleyle ilgili bir çerçeve var olması, homojen veya heterojen özelliğe sahip olup olmadığının sorgulanabilmesi ve heterojen ise her tabakadan yeterli sayıda birimin seçilip örneklem oluşturulması yöntemidir.

Kartopu örneklemesi

Özellikle bir çerçevenin mevcut olmaması ya da oluşturulmasının imkansız olması durumunda başvurulan bir yöntemdir. Örneğin bir bölgede uyuşturucu kullananların sayısını belirlemek gibi.

Olasılıklı örnekleme Yöntemleri

Her örnekleme birimine hesaplanabilir ve sıfırdan farklı bir olasılıkla seçilme imkanı veren örneklemedir.

Basit tesadüfi örnekleme

Her birime eşit seçilme şansı vererek oluşturulan bir örnekleme yöntemidir.

Sonsuz Ana kütlelerde Basit tesadüfi örnekleme

Bir poliklinikten hizmet alan hastalar gibi bir topluluğun, yani ana kütle sınırlarının çizilemediği bir topluluğun olduğu durumda, ilgilenilen değişken veya hastalığa göre oluşturulan örnekleme yöntemidir.

Tabakalı örnekleme

Ana kütle heterojen ise kendi içinde homojen olan her tabakadan tesadüfi yöntemle seçilen örneklemin oluşturulduğu yöntemdir.

Sistematik örnekleme

Tüm birimler birden N e kadar numaralandırılır. Örneklem hacmi n belirlenir. k=N/n oranı belirlenir.1,2,…., k adet sayı arasından tesadüfi bir tane seçilir. Çekilen sayı a ile gösterilsin. a, örnekleme girecek birinci birimdir. Bir sonraki birim a+k. terim olur. Her seferinde seçilen birimden k birim sonrası tekrar seçilir. Bu şekilde n hacimli örneklem oluşturulur. Oluşturulan örneklemden elde edilen veriler kullanılarak gerekli istatistikler hesaplanır. Bu sürece sistematik örnekleme denir.

Tek aşamalı ve çok aşamalı küme örneklemesi

Ana kütlenin birimleri çeşitli kümelerden oluşuyorsa, bu kümelerin arasından belirli sayıda küme seçilir ve seçilen kümenin tamamı örneklemi oluşturuyorsa bu tek aşamalı örnekleme yöntemidir. Birimlere ulaşmak için birden fazla kümeleme yapma ihtiyacı duyuluyor ise bu çok aşamalı örnekleme yöntemidir.

Örnekleme Dağılımı

Tesadüfi örneklemden hesaplanan ana kütle parametresinin tahmini değerinin olasılık dağılımına örnekleme dağılımı denir.

Ortalamanın ( 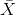’nın) örnekleme dağılımı

Örneklem ortalamasının olasılık dağılımına ortalamanın örnekleme dağılımı denir.

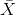’nın Dağılımının özellikleri

Bu dağılımın ortalaması µ ve standart sapması ?x ile açıklanır.

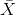’nın Dağılımının Ortalaması

• Örneklem arttıkça örnekleme dağılımının ortalaması ana kütle ortalamasına yaklaşır.
• Ana kütle dağılım şekli çarpık bir dağılım gösterse bile, örneklem hacmi arttıkça normal dağılıma yaklaşır.

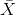’nın Dağılımının standart hatası

Standart hata ? 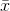ortalamanın örnekleme dağılımının değişkenliğini gösterir.

Merkezi Limit Teoremi

Ana kütle dağılım şekli ne olursa olsun, örneklem hacmi büyüdükçe, 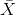dağılımı normal dağılım gösterir.

Örneklem oranı p’nin örnekleme dağılımı

Ana kütle oranı, ana kütlenin birimleri içindeki ilgilenilen türden özelliğe sahip olanların oranı olarak tanımlanır.

Ortalama ve varyans

Ana kütle oranı ? hakkında araştırılmak istenilen bilgi n hacimli tek bir örneklem için hesaplanan p istatistiğine değil, bir tesadüfi değişken olan p istatistiğinin örnekleme dağılımının özelliklerinden yararlanılarak üretilir. Varyans standart sapmanın karesidir.