Matematiksel İktisat Dersi 8. Ünite Özet
Kısıtlı Optimizasyon
Giriş
Sonsuz olan insan ihtiyaçları karşısında kaynakların kıt olmasından dolayı seçim yapmayı gerektirir. Yapılacak seçim bazen koşulsuz olacaktır. Koşulların olmadığı durumda yapılan seçime “kısıtsız optimizasyon” denir.
Fakat iktisatta seçim çoğu zaman kısıtlar altında yapılmak zorundadır. Tüketici bütçesini ve ürün fiyatlarını göz önünde bulundurup faydasını maksimize etmeyi amaçlayacak, firma maliyetlerini göz önünde bulundurup üretimini maksimize etmeye çalışacak, hükümetler enflasyonu yükseltmeden istihdamı artırmayı amaçlayacaktır. Bir amacın belirli kısıtlar altında gerçekleştirilmesine “kısıtlı optimizasyon” denir.
Kısıtlı optimizasyon matematiksel olarak ise bir fonksiyonu belirli kısıtlar altında minimum ya da maksimum yapan değerleri bulmak şeklinde tanımlanır.
Kısıtlı Optimizasyon
Bir kısıtlı optimizasyon problemi üç farklı şekilde çözülebilir. Bunlar:
- Yerine Koyma Metodu,
- Toplam Diferansiyel Metodu ve
- Lagrange Çarpanı Metodudur.
Yerine Koyma Metodu İle Kısıtlı Optimizasyon: f(x,y) amaç fonksiyonunu g(x,y) = k kısıtı altında optimize etmenin birini yolu kısıtı amaç fonksiyonu içerisine koymaktır.
g(x,y) = k, y = h(x,k) Amaç fonksiyonu:
f(x,h(x,k)) fonksiyonun x’e göre türevini alırsak:
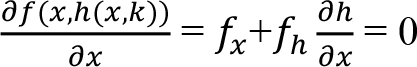 I.dereceden koşullara ulaşıldı.
I.dereceden koşullara ulaşıldı.
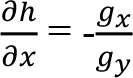 (Kapalı fonksiyon kuralından faydalanırsak)
(Kapalı fonksiyon kuralından faydalanırsak)
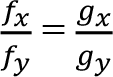
Kısıtlı optimizasyonda yerine koyma metodu, problemi kısıtsız optimizasyon problemine dönüştürür.
Toplam Diferansiyel Yaklaşımı İle Kısıtlı Optimizasyon: Bu yaklaşımda hem amaç fonksiyonunun hem de kısıtın toplam diferansiyeli alınıp eşanlı olarak çözülür.
Amaç fonksiyonumuz f(x,y) ve kısıt fonksiyonumuz g(x,y) = k. Her iki fonksiyonun toplam diferansiyeli:
df = 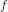 x dx +
x dx + 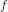 y dy
y dy
dk =  x dx +
x dx +  y dy = 0
y dy = 0
“k” bir sabit olduğundan kısıt fonksiyonunun toplam türevi sıfıra eşittir. İkinci eşitlikten;
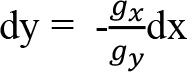 İfadeyi birinci eşitlikte yerine koyarsak;
İfadeyi birinci eşitlikte yerine koyarsak;
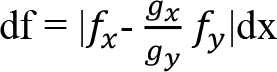 olur.
olur.
Birinci dereceden koşulların sağlanabilmesi için df = 0 olması gerekir. Bunun için ise:
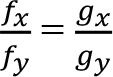 olması gerekir.
olması gerekir.
Lagrange Çarpanı Metodu İle Kısıtlı Optimizasyon:
f(x,y) amaç fonksiyonunu g(x,y) = k kısıtı altında optimize etmek için Lagrange Çarpanı (?) metodundan faydalanılır. Bu metotla yapılan çözümlerin özelliği amaç fonksiyonunu bir ya da birden fazla kısıt altında optimize eden değişkenlerin değerleri ile birlikte, kısıttaki değişimin amaca etkisini gösteren Lagrange çarpanıdır.
Lagrange metodu ile optimizasyon için:
- Öncelikle kısıt sıfıra eşitlenir: k - g (x, y) = 0 2.
- Sonra kısıt Lagrange çarpanı ile çarpılır ve Lagrange fonksiyonu oluşturulur:
L (x, y, ?) = f (x, y) + ?) {k - g (x, y)}
L (x, y, ?) Lagrange fonksiyonunu, f (x, y) amaç fonksiyonunu ve g (x, y) kısıtı temsil etmektedir. Lagrange fonksiyonundaki kısıt sıfıra eşit olduğundan, ? {k - g (x, y)} terimi de sıfıra eşittir. Dolayısıyla aslında Lagrange fonksiyonu amaç fonksiyonunun ta kendisidir. - Fonksiyonu optimize eden x, y ve ? değerlerini bulabilmek için ilk önce Lagrange fonksiyonunun birinci dereceden türevleri alınır ve sıfıra eşitlenir. Sonra çözümler eşanlı çözümlenir ve değerler bulunur.
Lagrange fonksiyonuna kısıtın ? {k - g (x, y)} ya da ? {g (x, y) - k} şeklinde yazılması sonucu değiştirmeyecektir. Bu sadece ?’nın işaretini değiştirecektir.
3 aşamalı optimizasyon süreci şöyledir:
L (x, y, ?) = f (x, y) + ? {k - g (x, y)}
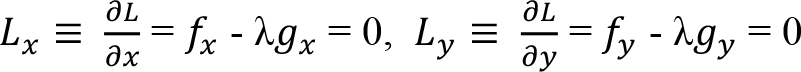
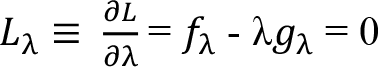 Koşullar eşanlı çözülürse:
Koşullar eşanlı çözülürse:
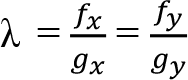 olur ve bu eşitlikten bir x ya da y değeri L ? fonksiyonunda yerine konarak amaç fonksiyonunu verilen kısıt altında optimize ederek x, y ve ? değerleri bulunur.
olur ve bu eşitlikten bir x ya da y değeri L ? fonksiyonunda yerine konarak amaç fonksiyonunu verilen kısıt altında optimize ederek x, y ve ? değerleri bulunur.
Lagrange Çarpanı’nın Anlamı: Lagrange çarpanı (?), amaç fonksiyonunun kısıt fonksiyonundaki değişime duyarlılığını ölçer.
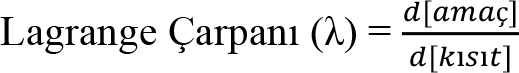
Karşı karşıya kalınan probleme göre Lagrange çarpanına farklı anlamlar yüklenecektir. Örneğin tüketicinin bütçe kısıtı altındaki fayda maksimizasyon probleminde, ? harcamanın marjinal faydasına işaret ederken, bir firmanın belirli bir üretim kotası altındaki maliyet minimizasyon probleminde ise üretimin marjinal maliyetini gösterecektir.
Çok Değişkenli Fonksiyonlarda Kısıtlı Optimizasyon
Amaç ve/veya kısıt fonksiyonlarındaki değişken sayısının ikiden fazla olduğu durumlarda Lagrange metodunu kullanarak kısıtlı optimizasyon problemlerini çözmek mümküdür. n değişkenli olan bir amaç ya da amaç fonksiyonumuz için:
f(x 1 , x 2 , …,x n ) ve n değişkenli kısıt fonksiyonumuz:
g(x 1 , x 2 , …,x n ) = k
L(x1, x2,..,xn, ?) = f(x1, x2,...,xn) + ?{k - g (x1, x2,.., xn)}
Birinci dereceden koşullar eşanlı olarak çözülürse:
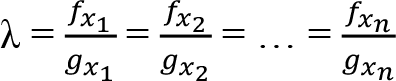
Çok Değişkenli Çok Kısıtlı Fonksiyonlarda Optimizasyon
Lagrange çarpanı metodu bir amaç fonksiyonunun birden fazla kısıtın olduğu durumlarda da kullanılabilir. Bu durumda kısıt kadar Lagrange çarpanı olacaktır.
n değişkenli amaç fonksiyonumuz;
f(x 1 , x 2 , …,x n ) ve
n değişkenli iki farklı kısıt fonksiyonumuz;
g(x 1 , x 2 , …,x n ) = k, z(x 1 , x 2 , …,x n ) = m Bu durumda:
L(x 1 , x 2 , …,x n , ? 1 , ? 2 ) = f( x 1 , x 2 , …,x n ) + ? 1 {k – g(x 1 , x 2 , …,x n )} + ? 2 {m – z(x 1 , x 2 , …,x n )}
Birinci dereceden koşullar yazılıp denklem sistemi eşanlı olarak çözülürse söz konusu kısıtlar altında amaç fonksiyonunu optimize eden x 1 * , x 2 * …, x n * , ? 1 * , ? 2 * bulunur.
İkinci Dereceden Koşullar
Kısıtlı optimizasyon problemlerinde elde edilen sonuçlar her ne kadar amaç fonksiyonunu optimize eden değerleri verse de bulunan noktanın fonksiyonun o kısıt altında maksimumda mı yoksa minimumda mı olduğu hakkında bilgi vermez. Bunu anlamak için Lagrange fonksiyonunun ikinci dereceden koşullarına bakılır. Bunun için Hessian matrisi oluşturup pozitif mi yoksa negatif mi olduğuna bakılır.
f(x, y) amaç fonksiyonunu g(x,y) = k kısıtı altında optimize etmek için Lagrange fonksiyonunun
L (x, y, ?) = f (x, y) + ? {k - g (x, y)}
Sınırlandırılmış Hessian matrisi aşağıdaki gibidir:
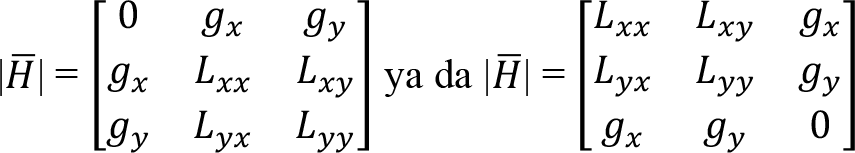
Kısıt altında optimize edilmiş amaç fonksiyonunun minimum mu yoksa maksimum mu olduğunu belirlemek için, sınırlandırılmış Hessian’ın asal minörlerine bakılır. Sınırlandırılmış Hessian’ın bütün asal minörleri negatifse, yani: {| 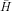 2 | < 0, |
2 | < 0, | 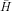 3 | < 0,…, |
3 | < 0,…, | 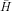 n | < 0} ise amaç fonksiyonu minimumdadır.
n | < 0} ise amaç fonksiyonu minimumdadır.
Eğer asal minörler pozitiften başlayarak işaret değiştiriyorsa yani: {I 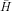 2 | > 0, |
2 | > 0, | 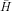 3 | < 0,…, (-1) n I
3 | < 0,…, (-1) n I 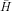 n | > 0} ise sınırlandırılmış Hessian negatif belirli ve Lagrange fonksiyonu maksimumdadır.
n | > 0} ise sınırlandırılmış Hessian negatif belirli ve Lagrange fonksiyonu maksimumdadır.
Kısıtlı Optimizasyon İle İktisadi Uygulamalar
Tüketicinin fayda maksimizasyon problemi, bireylerin çalışma-boş zaman tercihi, firmanın kapasite kısıtı altında kâr maksimizasyon problemi, girdi fiyatları sabit ve firmanın finansman olanakları sınırlı iken üretimin maksimize edilmesi ya da belirli bir üretim düzeyinin maksimize edilmesi ya da belirli bir üretim düzeyinin en düşük maliyetle gerçekleştirilmesi ve bunlara benzer birçok iktisadi mesele kısıtlı optimizasyon teknikleri kullanılarak çözülebilir.
Tüketicinin Fayda Maksimizasyonu: Tüketicinin problemi faydasını maksimize etmektir. Tüketicinin x ve y gibi iki mal tükettiğini ve bu malları Px ve Py fiyatlarından satın alabildiğini varsayalım. Tüketicinin fayda fonksiyonunu, yani amaç fonksiyonunu:
U = U(x,y) Tüketicinin bütçesini M ile gösterirsek, kısıt fonksiyonu: M = P x X + P y Y Bu durumda:
Maksimize et: U = U(x,y)
Kısıt: M = P x X + P y Y
Problemi “yerine koyma” ya da “toplam diferansiyel” ya da “Lagrange” metotlarından herhangi biri ile çözmek mümkün olsa da Lagrange metodunun üstünlüğü nedeniyle tüketicinin optimizasyon problemini Lagrange metodu ile çözelim. I. Dereceden koşullar:
L (x, y, ?) = U(x,y) + ?(M - P x x - P y y )
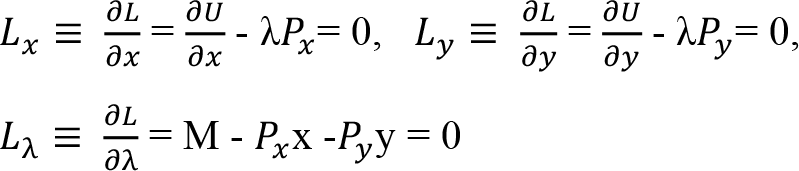
Bu göre; 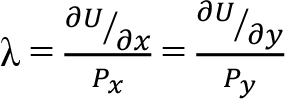
Buna göre bir malın tüketilen son biriminin tüketiciye sağladığı faydaya o malın marjinal faydası denir. Dolayısıyla x malının marjinal faydası 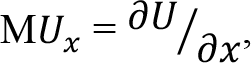 , y malının marjinal faydası
, y malının marjinal faydası 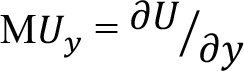 ’dir. Buradan;
’dir. Buradan; 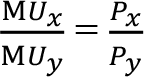 buna tüketicinin fayda optimizasyonu veya tüketici dengesi denir. Şu şekilde de gösterilir:
buna tüketicinin fayda optimizasyonu veya tüketici dengesi denir. Şu şekilde de gösterilir:
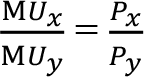
İki mal tüketen bir tüketicinin bu iki maldan sağladığı marjinal faydaların birbirine oranına marjinal ikame oranı (MRS) denir. Bu durumda eşitlik;
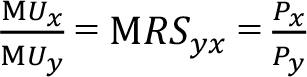
Tüketicinin faydasını bütçe kısıtı altında maksimize ederek elde edilen talep fonksiyonlarına bayağı (Marshalgil) talep fonksiyonları denir. x ve y malları bayağı talep fonksiyonları aşağıdaki gibidir:
X malı bayağı talep fonksiyonu: X M * = X (P x , P y , M)
Y malı bayağı talep fonksiyonu: Y M * = Y (P x , P y , M)
Tüketinin Harcama Minimizasyonu
Tüketici her zaman faydasını maksimize etmeyi amaçlamak yerine belirli bir fayda düzeyine minimum harcamayla ulaşmayı hedefleyebilir. Bu durumda amaç fonksiyonu tüketicinin bütçe fonksiyonu iken, kısıt fonksiyonu da fayda fonksiyonu olacaktır.
İki mal tüketen bir tüketicinin bütçe fonksiyonunu M = P x x + P y y ve fayda fonksiyonu U = U(x,y) ise;
Minimize et: M = P x x + P y y
Kısıt: 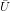 = U(x,y)
= U(x,y)
Paydanın(U) üzerindeki tire işareti tüketicinin faydasının sabit olduğunu göstermektedir.
Harcama minimizasyonu durumunda Lagrange fonksiyonu:
L (x, y, ?) =P x x + P y y + ?( 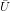 - U(x, y))
- U(x, y))
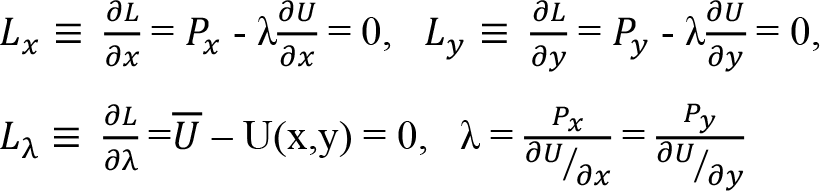
İki mal tüketen bir tüketici ister belirli bir bütçe ile faydasını maksimize etmek istesin, isterse belirli bir fayda düzeyine minimum harcama ile ulaşmayı hedeflesin, her iki durumda da malların marjinal faydalarının fiyatlarına oranı birbirine eşit olmalıdır. Yani tüketici optimumu için;
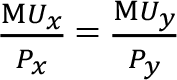 ya da
ya da 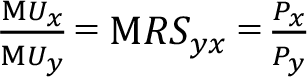
Tüketicinin belirli bir faydayı en düşük harcama ile elde etmesini sağlayacak talep fonksiyonları, malların fiyatları ile birlikte tüketicinin fayda düzeyinin bir fonksiyonudur ve Hicksgil talep fonksiyonları aşağıdaki gibidir:
x malı Hicksgil talep fonksiyonu: X H * = X (P x , P y , 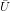 )
)
y malı Hicksgil talep fonksiyonu: Y H * = Y (P x , P y , 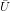 )
)
Firmalarda Kısıtlı Optimizasyon: Firmaların karşı karşıya kaldığı en temel kısıtlı optimizasyon problemlerinden bazıları şöyle sıralanabilir:
- Belirli bir üretim düzeyini en düşük maliyetle gerçekleştirmek,
- Faktör fiyatları ve üretim teknolojisi veri iken maksimum üretimi sağlayacak faktör bileşimini belirlemek,
- Kapasite kısıtı altında karını maksimize etmek.
Bunların dışında firmalar rakip firmaların da kararlarını ve tepkilerini dikkate almaları gereken farklı optimizasyon problemleri ile karşı karşıya kalabilir.
Maliyet Miimizasyonu: Emek(L) ve sermaye(K) olmak üzere iki girdi kullanan bir firmanın üretim fonksiyonu:
q = q(K,L) Bu firmanın sermayeyi P K ve emeği P L fiyatlarından satın aldığını varsayarsak toplam maliyet fonksiyonu TC = P K K + P L L.
Buna göre firmanın problemi:
Minimize et: TC = P K K + P L L.
Kısıt: 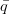 = q(K,L)
= q(K,L)
Lagrange fonksiyonu ve I. Dereceden koşullar aşağıdadır:
L (K, L, ?) = P K K+ P L L+ ?( 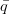 - q(K, L))
- q(K, L))
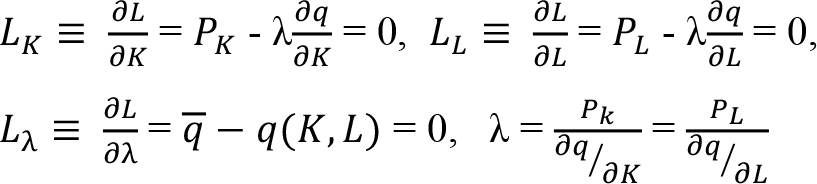
Üretimde iki faktör kullanan ve belirli bir üretim düzeyini en düşük maliyetle gerçekleştirmek isteyen bir firma üretimde kullandığı faktörlerin marjinal fiziki verimlerinin oranını (MRTS) faktörlerin fiyat oranına eşitlemelidir.
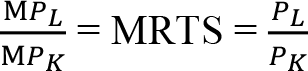
Üretim Maksimizasyonu: Firmaların diğer bir optimizasyon problemi, sınırlı parasal olanaklarla, yani sınırlı sermaye ile üretimlerini maksimize etmeleridir. Bu problem maliyet minimizasyon probleminin tersidir. Burada firmanın amaç fonksiyonu üretim fonksiyonu iken, kısıtı maliyet fonksiyonudur.
Maksimize et: q = q(K,L)
Kısıt: TC =P K K + P L L
-
2025-2026 Bahar Dönemi Ara (Vize) Sınavı İçin Sınav Merkezi Tercihi
date_range 9 Gün önce comment 3 visibility 494
-
AÖF 2025-2026 Öğretim Yılı Bahar Dönemi Kayıt Yenileme Duyurusu
date_range 1 Şubat 2026 Pazar comment 3 visibility 321
-
2025-2026 Öğretim Yılı Güz Dönemi Ara (Vize) Sınavı Sonuçları Açıklandı!
date_range 16 Aralık 2025 Salı comment 5 visibility 825
-
2025-2026 Güz Dönemi Dönem Sonu (Final) Sınavı İçin Sınav Merkezi Tercihi
date_range 3 Aralık 2025 Çarşamba comment 3 visibility 813
-
2025-2026 Güz Dönemi Ara (Vize) Sınavı Sınav Bilgilendirmesi
date_range 2 Aralık 2025 Salı comment 2 visibility 668
-
Başarı notu nedir, nasıl hesaplanıyor? Görüntüleme : 26803
-
Bütünleme sınavı neden yapılmamaktadır? Görüntüleme : 15411
-
Harf notlarının anlamları nedir? Görüntüleme : 13583
-
Akademik durum neyi ifade ediyor? Görüntüleme : 13379
-
Akademik yetersizlik uyarısı ne anlama gelmektedir? Görüntüleme : 11159