Halkla İlişkiler Araştırmaları Dersi 6. Ünite Özet

Nicel Veri Çözümleme

Nicel veri çözümleme sayıları nasıl anlamlı bilgi hâline getirebileceğimizi gösteren bilgiler bütünü olarak ele alınabilir.

İnceleme yapılan konudaki grupların doğalarını, yapılarını anlayabilmek için elimizde öncelikle sayısal bilgiler, ölçümler kısacası veriler olması gerekmektedir. Gerçek nesne, birey veya olayları ölçmek, gözlemlemek veya saymakla elde edilen sayılara veri adı verilir. Veriler nüfus sayımları, kamuoyu araştırmaları, seçim anketleri, reyting araştırmaları, sanayi sayımları gibi araştırmalardan elde edilebilir.

İletişim alanında veri toplama yöntem ve araçları arasından en çok kullanılanları anket ve ölçeklerdir. Veri toplamada önemli olan hangi yöntemin araştırmacının amaçlarına en iyi şekilde hizmet edeceğinin belirlenmesidir.

Anket: Akademik, ticari ve resmî amaçlarla sıklıkla kullanılan ve giderek yaygınlık kazanan anket yanıtlayanın daha önce belirlenmiş bir sıralamada ve yapıda oluşturulan sorulara karşılık vermesiyle veri elde etme yöntemidir.

Anket çalışmasında belki de en zor safha anketin hazırlanmasıdır. Sorular herkes tarafından anlaşılacak biçimde kısa, açık ve kesin olmalıdır. Anket sorularını hazırlamada geçerli iki ana ilke vardır. Bunlardan birisi, sorulacak her sorunun araştırmanın ana konusu veya hipotezi ile doğrudan ilişkili olması, ikincisi ise soru listesinin bir iç bütünlüğe sahip bulunmasıdır. Bu ilkelerden birincisi, ilgisiz soruların sorulmamasını, ikincisi de birbirine benzer soruların kendi aralarında gruplandırılmalarını ve dolayısıyla soru listelerinin mantıklı bir bütünlük oluşturmasını hedefler. Anket süreci, problemin ifade edilmesi ile başlar. Daha sonra ankete katılacak kişiler belirlenir. Anketin geçerliği kabul edilebilir düzeyde ise anketin uygulanması sürecine geçilir. Anket gerçekleştirildikten sonra verilerin değerlendirilmesi bilgisayar yazılımları kullanılarak yapılır.

İnternet anketi kapsam dışı bırakıldığında anket yöntemleri üçe ayrılır:

• Yüz yüze Anket
• Telefonla Anket
• Postayla Anket

Yüz Yüze Anket: Bir anketörün cevaplayanla iletişime geçtiği yüz yüze anket en güvenilir veri toplama yöntemleri arasında yer alır. Bazen cevaplayanların karşısında bir anketör yerine bir bilgisayar da olabilmektedir. Yüz yüze anketin avantajları; Cevaplama oranı yüksek olması, cevaplayıcı ile kurulan yakın ilişki ile güvenilir ve doğru veriler toplanması, anketörlerin gözlenmesi ile verilerin doğruluğunu kontrol etmenin mümkün olması, anlaşılmayan soruları anketörün açıklama imkânının olması, görsel malzemeler kullanabilme imkânı sağlaması olarak sayılabilir. Dezavantajları ise cevaplama süresinin uzun olması, veri toplama maliyetinin yüksek olması, anketör ve cevaplayıcılardan kaynaklanan hatalara açık olması, anketörün iyi eğitilmesi zorunluluğu, zaman alıcı bir yöntem olması olarak sayılabilir.

Telefonla Anket: Anketörün cevaplayıcı ile telefon, faks ya da sesli posta iletişim araçlarını kullanarak gerçekleştirilen anketlerdir. Geniş coğrafi dağılımlarda anket yapılması gereken durumlarda kolaylık sağlayan bir tekniktir. Telefonla anket, sorular kısa olduğunda ve cevaplayıcı cevaplamayı kabul ettiğinde araştırma için uygun bir tekniktir. Kapsama alanı geniştir. Veri toplama süresi hızlıdır. Seyahat masrafı yoktur. Yüz yüze iletişimden kaynaklanacak tedirgin edici sorulara daha kolay yanıt alınabilir. Dezavantajları ise araştırma sadece telefonu olan kişiler ile sınırlıdır. Cevaplayıcıların demografik özellikleri önceden saptayarak örnekleme yapmak mümkün değildir. Anket süresi kısa olması gerektiği için detaylı anket yapılarına uygun değildir. Anketin cevaplayıcı tarafından yarıda bırakılma ihtimali fazladır. Anket görsel kullanımına uygun bir teknik değildir. Telefonla ankette cevaplama oranı şu şekilde hesaplanır;

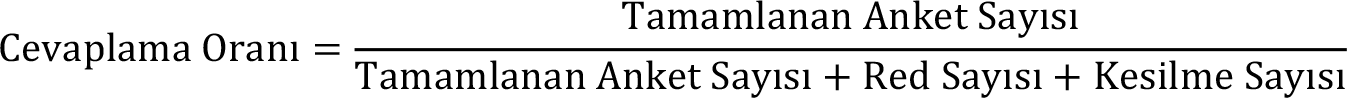
Posta ile Anket: Cevaplayıcıya posta ile ulaşılarak cevaplayıcının anketi kendi doldurduğu bir yöntemdir. Diğer iki anket tekniğine göre daha az maliyetlidir. Yoğun iş temposunda çalışan insanlar ile görüşülmesi gereken çalışmalarda en uygun tekniktir. Posta ile anketin avantajları; anketör faktörünün olmaması, cevaplayıcının kendi belirlediği zamanda anket formunu doldurabilmesi, geniş bir coğrafik alanda veri toplama için uygun olması, seyahat gerektirmemesidir. Dezavantajları ise cevaplama oranı çok düşük olması, cevaplama anında anketi kimin doldurduğu, sorulara verilen cevapların doğru olup olmadığı bilinmemesi, veri toplamanın zaman alması, cevaplama oranı düşük olduğunda geri dönen anketlerin formu başına maliyet yükselmesi, sorular anlaşılmadığında cevaplayıcıya açıklama olanağının olmaması, tutumların hızlı değişmesi nedeniyle bu tip konular için yavaş bir yöntem olması, zaman bakımından kısıtlı süre olan çalışmalara uygun olmamasıdır. Geri dönüş oranı şu şekilde hesaplanır;

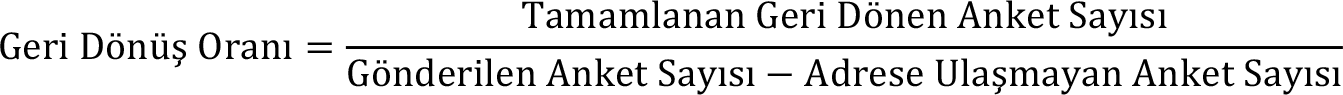
Posta ile anket uygulamalarında geri dönüş oranı %30 ve üzerinde ise bu oran iyi bir oran kabul edilmektedir.

Özel posta ile anket tekniği; e-posta yoluyla anket: Günümüzde elektronik posta kullanımın artması ile e-mail yolu ile anketler de kaçınılmaz olarak araştırmacıların sıklıkla başvurduğu bir teknik olmuştur. Türkiye’de yaşayan insanların yaklaşık %60’ının İnternet kullanımı olması nedeniyle bu tekniğin kullanımı ülkemizde de giderek artmaktadır. Burada da dikkat edilmesi gereken nokta, araştırmanın sadece e-postaya sahip insanlar ile sınırlı olmasıdır. Anket sorularının e-posta ile gönderilmesi biçiminde uygulanır. Posta ile anketin avantaj ve dezavantajı bu teknik içinde geçerlidir.

Ölçme ve Ölçekler

İkincil kaynaklar kullanılarak oluşturulan verilerde çoğunlukla ölçme işleminin büyük bir kısmı hazır olarak elde edilebilir. Çalışma konusuna göre, gerektiğinde veriler sadece düzenlemeye ihtiyaç duyabilirler. Ama araştırmacının veriyi kendisi oluşturması gerektiğinde araştırmacı kendi ölçme tekniğini geliştirmek ve ölçek hazırlamak durumundadır.

Ölçme, kişilerin ya da nesnelerin özelliklerine puan veya sayı verme işlemi olarak tanımlanabilir. Birçok ölçme ve ölçeklendirme tekniği bulunmaktadır. Bir tekniği doğru olarak uygulama yolunu anlamak çok önemlidir. Nicel veriler sayısal biçimdedir ve ölçme, verilerin sayılara dönüştürülmesidir. Dünyaya ilişkin veriler gerçekte sayılar biçiminde değildir. Verilerin sayısal hâle getirilebilmesi ve böylece araştırılabilir bir yapı oluşturulması ölçme ile gerçekleştirilir. Ölçme ile önceden tespit edilen kurallar çerçevesinde nesnelerin ve kişilerin özelliklerine sayılar ya da semboller atama yapılır. Ölçülmek istenen özelliğin karmaşıklığı ve soyutluğuna bağlı olarak değişik seviyede ölçümler yapmak, farklı ölçekler kullanmak mümkündür. Düşük ölçüm seviyelerinde ölçüm yapıldığında elde edilen veriler ile pek fazla istatistiksel analiz yapılamaz.

Ölçme sadece niceliksel verilere uygulanmaz. Bazen subjektif kavramları da ölçme ihtiyacı doğabilir. Bunlar kişilerin veya nesnelerin özellikleri ya da nitelikleri biçiminde olabilir.

Bireylerin tutum, değer, tercih ve inanç gibi duygusal alandaki eğilim ve yönelimlerini belirlemek amacıyla kullanılan veri toplama araçlarıdır. Ölçek geliştirilirken ölçekteki madde sayılarının insanları yoracak kadar çok olmaması, ifadelerin açık ve anlaşılır biçimde yazılması, kısa cümlelerin yeğlenmesi, her maddede yalnızca tek konu hakkında yanıt istenmesi, gerekirse maddelerin belirli kategoriler altında toplanması, olumlu ve olumsuz ifadelerin iyi harmanlanması, seçeneklerin tutarlı biçimde düzenlenmesi, orta noktaların kararsızlık ve dengelerinin belirtilmesi ve her yanıtın bir puan değerinin olması gibi konularda dikkat edilmelidir. Ölçme işleminde kullanılan dört temel ölçek bulunmaktadır. Bunlar; sınıflama ölçeği, sıralama ölçeği, aralıklı ölçek ve oranlı ölçek olarak adlandırılırlar. İlk iki ölçek olan sınıflama ve sıralama ölçekleri kategorik ölçeklerdir. Aralıklı ve oranlı ölçek ise metrik ölçeklerdendir.

Sınıflama Ölçeği: Sayıların niceliksel olarak bir anlam taşımadığı sadece bir etiket biçiminde kullanıldığı ölçek türüdür. Bu ölçek türü verilen cevapların kategorilerini oluşturmada kullanılır. Birimleri veya nesneleri sınıflayabiliriz. Sayılar cevapların birbirinden üstünlüğünü göstermez. Sadece onları sınıflar.

İstatistik, analizlerin kullanımı açısından dört ölçek türü içinde en zayıf olanıdır. Sınıflama ölçeğinde verilerin sırası, uzaklığı ve orijini olmadığı için sınırlı sayıda istatistik hesaplanabilir. Bu ölçek ile elde edilmiş verilerin aritmetik ortalamasını hesaplamak anlamlı olmaz. Çünkü hiçbir önemi yoktur. Sadece en çok tekrar eden değer anlamına gelen mod değeri alınabilir. Sıralama ölçeği kullanılarak elde edilmiş verilerin frekans tabloları incelenebilir.

Sıralama Ölçeği : Bir nesnenin diğer bir nesneye göre bir özelliğe daha fazla, daha az ya da aynı oranda sahip olduğunu söyleyebildiğimiz ölçek türüdür. Sıralama ölçeğinde veriler arasında sıralama yapmak mümkündür. Bu ölçekte sayılar, temsil ettikleri olguların sırasını gösterir. Sıralama ölçeği aynı zamanda sınıflama ölçeğinin işlevini de gerçekleştirebilen bir ölçektir. Yani sıralama ölçeği veriler hem sıralayabilir, hem de sınıflayabilir. Sıralama ölçeği, sınıflama ölçeğinden daha güçlü bir ölçektir. Çünkü burada sayılar sıralama özelliğine sahip oldukları için, bir nesnenin özelliği diğer bir nesnenin özelliğinden az, fazla ya da eşit olabildiğini söyleyebilme imkânı doğar. Sıralama ölçeği de sınıflama ölçeğinde olduğu gibi verilerin frekans tabloları ve mod değerleri bulunabilmesinin yanı sıra medyan değerini de hesaplamak mümkündür. Ancak verilerin aritmetik ortalamasını bulmak mümkün değildir. Çünkü atfedilen sayıların arasındaki uzaklıklar belli ve eşit değillerdir.

Aralıklı Ölçek : Aralıklı ölçek, başlangıç noktası önceden belirlenmiş ve olguları temsil eden sayıların arasındaki uzaklıkların eşit olduğu bir ölçektir. Sıralama ölçeğinden daha güçlüdür. Çünkü sınıflama ve sıralama ölçeklerinde bulunan bütün özellikleri taşır ve ayrıca ölçme değerleri arasındaki farkları anlamlı bir şekilde yorumlama imkânı tanır. Bir nesnenin bir özelliğe diğer bir nesneye göre ne kadar fazla sahip olduğunu gösterir. Bu ölçekte, iki veya daha fazla nesnenin özelliğe göre birbirine ne kadar uzak olduğunu söylemek mümkündür. Aralıklı ölçekle ölçülmüş veriler düzen ve uzaklık özelliklerine sahiptir. Aralıklı ölçek, istatistik olarak da pek çok analizin yapılabildiği bir ölçektir. Bu ölçek ile ölçülmüş verilerde aritmetik ortalamayı hesaplamak anlamlıdır. Ayrıca aritmetik ortalamadan sapmayı ölçmek için standart sapma hesaplanabilir. Ama aralıklı ölçekle ölçülmüş veriler, nesneler arasında mutlak büyüklük karşılaştırması yapmaya izin vermezler. Çünkü bu ölçekte gerçek bir sıfır noktası yoktur. Aralıklı ölçekte sıfır noktasının yeri sabit değildir.

Oranlı Ölçek : Gerçek bir sıfır noktası olan bir ölçektir. Burada sıfır değeri anketi cevaplayan herkes için aynı anlamı ifade etmektedir. Bu özelliği sayesinde diğer üç ölçekten oldukça güçlüdür. Oranlı veriler genellikle doğrudan gözlenebilir fiziksel olaylarda ya da varlıklarda kullanılır. Çok yönlü bir ölçek olup yukarıda belirtilen her üç ölçek türünü de kapsar. Bu ölçek ile her türlü ortalamanın hesaplanması ve her türlü istatistiksel analizin yapılması mümkündür. Sayısal olarak cevaplandırılan bütün açık uçlu sorular oranlı ölçek kategorisine girer.

Gerçek sıfır noktası olan bir ölçek olduğu için ölçekte bir olguyu temsil eden sayı, belirli bir büyüklüğü veya uzaklığı ifade eder.

Özel Ölçekler

Daha çok pazarlama ve iletişim alanlarında kullanılan ölçeklerdir.

Likert Ölçek : 1970 yılında Likert tarafından bulunan bu ölçek, tüketicinin bir nesne, bir tutum ya da bir davranış konusunda kendisine sunulan ifadelere katılma ya da katılmama derecesini ölçer. Burada her ifade karşısında “Kesinlikle katılıyorum” dan başlayan “Kesinlikle katılmıyorum”a kadar devam eden beş dereceli bir ölçek bulunmaktadır. Genellikle ifadeler 20-30 taneden oluşur. Likert ölçek 7’li, 9’lu ya da 11’li olabilir ama sıklıkla kullanımı 5’li Likert ölçeğidir. Aralıklı ölçek temeline dayanır.

Semantik Farklılık Ölçeği : Bu ölçekte çeşitli sözcüklerin ve kavramların algılanan anlamlarının üç faktöre göre ayrıştırılması söz konusudur. Bunlar; etkinlik, faaliyet ve değerlendirmedir. Aralıklı ölçek temeline dayanır. Bu ölçek çoğunlukla ürün ve hizmetleri çevreleyen imaj unsurlarına yönelik tutumları ölçmek için kullanılır. Sıfat tamlamaları kullanmak da mümkündür. Olumlu ve olumsuz sıfat ifadeleri sol ve sağ kutuplara tesadüfi olarak dağıtılır. Cevaplayıcılardan iki kutuplu sıfat çiftleri dizisinde yedi kategori arasından düşüncesini en iyi temsil edeni işaretlemeleri istenir. Her bir iki kutuplu sıfat çiftinin değerlendirilmesi genellikle incelenen nesnenin profilini ya da imajını çıkartmak için kullanılır. Bu da her bir nesneye ait her iki kutuplu sıfat çiftinin ortalama değerini hesaplayarak elde edilir. Böylece ikili karşılaştırmalar yapmak mümkündür.

Sabit Toplam Ölçeği : Bu ölçekte ise görüşülen kişilerden kendisine verilen sabit bir puanı belirlenmiş özelliklere göre nesnelere dağıtmaları istenir. Dağıtım sırasında tek bir özellik kullanılabildiği gibi birden fazla özelliğin de kullanılması mümkündür. Cevaplayıcının sıkılmamasını göz önünde tutarak nesnelerin sayısı fazla ise özelliklerin sayısı az tutulmalıdır. Puanlarda genellikle bölüştürme kolay olduğu için 10, 100 ve 1000 gibi rakamlar kullanılır. Aralıklı ölçek temeline dayanır.

Ölçeklerin Nitelikleri

Ölçekler konusunda üç tane özellik bulunmaktadır. Bu da istatistiksel olarak çok önemli kavramlar olan “Geçerlilik”, “Güvenilirlik” ve “Duyarlılık” kavramlarıdır. Bir ölçeğin geçerliliği, güvenilirliği ve duyarlılığı ne kadar yüksek ise o ölçek güçlü bir ölçek hâlini alır.

Geçerlilik: Geçerlilik toplanan verilerin tarafsızlığının ve ölçülen olayın, değişkenin niteliklerine uygunluğun ölçüsüdür. Diğer bir değişle bir ölçü aracının ölçtüğünü öne sürdüğü değişkeni ne derecede ölçtüğüdür. Bir ölçek ölçülmek istenen şeyi ölçüyor ise geçerli bir ölçektir. Bir ölçeğin geçerliliği hakkında bir yargıya varabilmek için üç farklı geçerlilik esas alınarak değerlendirmeler yapılır. Bunlar; uyum geçerliliği, içerik geçerliliği ve yapısal geçerliliktir.

Uyum Geçerliliği : Yeni geliştirilen bir ölçüm aracı ile aynı amaca yönelik bir başka ölçüm aracı arasındaki uyumun derecesini göstermektedir. Bazı ölçüm araçları kullanım zorluğu, maliyet gibi nedenlerden dolayı tercih edilmeyebilir. Bu durumda yeni bir ölçü aracı geliştirebilir. İki ölçü aracının uyum geçerliliği varsa bunlar birbiri yerine kullanılabilir.

İçerik Geçerliliği : Ölçeğin içeriğinin en azından görünümünün ne derece geçerli olduğunun ölçüsüdür. Kavramsal tanımlamanın ölçülmesinde tanımın içeriğini belirlemek ve tanımın içeriğindeki tüm ögeleri örnekleyen ölçümler geliştirmek gerekmektedir. Bu geçerliliği incelerken genellikle konuyla ilgili uzman kişilere danışılarak onların ölçek hakkında düşünceleri alınır.

Yapısal Geçerlilik : Gözlenemeyen ancak kuramsal olarak açıklanan bir psikolojik yapıyı ölçmeyi hedefleyen bir ölçü aracının amacına ne denli ulaştığıdır. Yapı geçerliliği analizi karmaşık ve çok yönlü bir süreçtir. Kuramsal olarak varlığı öne sürülen yapının, davranışlara ne derece yansıdığının ve ölçü aracının maddelerinin özelliklerinin incelenmesini gerektirir.

Güvenilirlik: Güvenilirlik, ölçme sonuçlarının farklı zamana ve koşullara karşı sahip olduğu tutarlılığı gösterir. Bir ölçek farklı zamanlarda veya farklı gruplarda aynı sonuçları ne kadar yüksek oranda veriyorsa o kadar güvenilir demektir. Güvenilirlik, istatistiksel analizlerle yüzde olarak hesaplanmaktadır. Bunun için ölçeğin birden fazla uygulaması yapılır ve sonuçların hangi ölçüde tutarlı olduğu saptanır. Güvenilirliğin istatistiksel ölçüsü Cronbach Alfa Değeri olarak isimlendirilir. Bu değer hazır istatistiksel programlar ile hesaplanmaktadır. Genelde bir ölçü aracının güvenilirlik düzeyinin %70 ve üstü olması istenmektedir. Güvenilirliğin önemi şu maddeler ile ifade edilebilir:

• Gözlenmiş ölçüm sonuçları, tahmin etmek istediğimiz doğru sonuçlardan ve hatalardan oluşur.
• Hata ne kadar küçükse gözlenen sonuçlar gerçek sonuca o kadar yakın olur.
• Güvenilirlik bize hatayı tahmin etme imkânı verir.
• Güvenilirlik ile hata arasında karşılıklı bir ilişki vardır. Güvenilirlik ne kadar yüksekse hata o ölçüde küçük ne kadar düşükse hata o derece yüksektir.

Güvenilirlik, ölçmede temel ve basit olarak tutarlılık anlamına gelir. Bu tutarlılığın dört yönü bulunmaktadır. Bunlar:

• Zamana Karşı Tutarlılık
• Madde Gruplarına Karşı Tutarlılık
• Değerlendiricilere Karşı Tutarlılık
• Maddelerin Tutarlılığı

Zamana Karşı Tutarlılık : Buna Ölçme-Tekrar Ölçme Güvenilirliği de denir. Ölçmenin zaman içindeki değişmezliği anlamına gelir ve genelde şu soruyla ifade edilir: “Aynı insanlarla aynı koşullar altında ancak farklı zaman diliminde aynı araç kullanılırsa bu araçlarla aynı sonuçlara ne ölçüde ulaşılacaktır?” Ölçüm aracıyla aynı sonuçlar elde edilebildiği oranda araç güvenilirdir. Burada aynı ölçü aracı bir süre arayla aynı bireylere iki kez uygulanır. İki testin arasındaki tutarlılık istatistiksel analizlerle hesaplanır.

Madde Gruplarına Karşı Tutarlılı k: Buna Eşdeğerli Ölçüm Güvenilirliği de denir. Bir ölçü aracının, birbirinin yerine kullanılabilecek iki ya da daha fazla formu oluşturulur. Ve ölçü aracının formları arasındaki uyum istatistiksel analizler ile incelenir. Aynı bireylere ölçü aracını sık sık uygulamanın gerekeceği durumlarda, ezberleme ve kanıksama gibi etmenleri kontrol etmek amacıyla her uygulamada ölçü aracının farklı bir formunun kullanılması amaçlanır.

Değerlendiricilere Karşı Tutarlılık : Değerlendiriciler arası Güvenilirlik; Ölçü aracının uygulanması ve puanlanması, değerlendiricinin becerisine dayalı ya da değerlendiricinin yorumunu gerektiriyorsa değerlendiriciler arası güvenilirliğin hesaplanması gerekir. Bu amaçla iki farklı değerlendiricinin aynı bireye aynı ölçü aracını uygulaması sonucunda elde ettiği puanlar arasındaki uyuşma, istatistiksel analizlerle belirlenir.

Madde Güvenilirliği : Ölçü aracının her bir maddesinin toplam puana yapmış olduğu katkı, iç-tutarlılık katsayısı olarak hesaplanır. Toplam puana belli düzeyde katkıda bulunmayan maddeler ölçü aracından çıkartılır. Bütün soruların ne ölçüde aynı şeyi ölçtüğünü değerlendirmek için çeşitli teknikler geliştirilmiştir. En iyi bilinenleri, sınamak yeniden sınamak ve Cronbach Alfa Katsayısı, tutarlılığın iki farklı yönünü gösterir. Bir ölçüm aracının güvenilirliğini sınamak için her ikisi de aynı anda veya teki kullanılabilir.

Duyarlılık: Duyarlılık, ölçeğin ne kadar hassas ölçmeler yapabildiğinin ölçüsüdür. Ölçmede “duyarlılık” bir ölçüm aracının insanlar arasındaki farklılıkları yakalayabilmesi- insanları ayrımlaştırabilmesi ve değişim yaratabilmesi- anlamına gelir. Eğer yaptığımız araştırmalarda değişimler önemli ise mümkün olduğunda en duyarlı ölçeği kullanmak gerekir. Ölçeğin duyarlılığını arttırmak için ölçeğe yeni nitelikler eklenebilir. Burada önemli olan cevaplayıcıyı zorlayacak ölçüde ayrıntılı ölçeklerden kaçınmaktır.

Nicel Veri Çözümleme Teknikleri

Nicel veri çözümlemesinde öncelikle verilerin analiz için hazırlanması ve düzenlenmesi gerekmektedir. Bilgisayar programları yardımı ile verilerin analizi mümkündür. Bu nedenle öncelikle veriler, kullanılan veri toplama aracında (anket ya da ölçek) cevaplayıcıların verdiği yanıtlara sayısal değerler verilerek kodlama yapılarak bilgisayara girişinin yapılması gerekir. Bu amaca yönelik olarak SPSS, Minitab, R, Lisrel gibi istatistiksel paket programlar kulanıldığı gibi herkesin kolaylıkla ulaşabileceği Excel programını da kullanılabilir. Excel ile basit düzeydeki istatistiksel işlemleri yapmak mümkündür.

Veri girişi yapıldıktan sonra ankette eksik veri olup olmadığı, hatalı veri girişinin olup olmadığı mutlaka kontrol edilmelidir. Hatalı veri girişinin kontrolü için Excel’de her soru için küçükten büyüğe sıralama yapılarak hatalı verilerin tespit edilmesi sağlanabilir. Bu durumda o cevaplayıcının orijinal anket formuna bakılarak cevap düzeltilmelidir. Düzeltme yapmak mümkün değilse o cevaplayıcın cevaplarının tamamı veri setinden çıkartılmalıdır. Süreksiz değişkenlerde boş ya da hatalı veri varsa doğru veri bilinmediği sürece bu veriler ilgili analizlerin dışında tutulurlar. Sürekli değişkenlerde de hatalı verilerin analiz dışında tutulması en doğrusudur. Öte yandan katılımcı sayısının önem taşıdığı analizlerde böyle bir dışlama işlemi sonucunda çok sayıda katılımcı kaybedilebilir. Böyle bir endişe varsa hatalı verilerin bulunduğu hücrelere değişkenin aritmetik ortalamasının yazılması da önerilebilir. Hatalı değişken miktarı toplam katılımcıların yüzde 15’ine ulaşmadığı sürece böyle bir işlemin sorun yaratmayacağı öne sürülmektedir.

Genel olarak bakıldığında nicel araştırmalarda iki tür veri çözümleme tekniği bulunmaktadır. Bunlar; Betimsel İstatistikler ve Yordamsal İstatistiklerdir. Amacımız, tek bir sorunun, maddenin ya da değişkenin aldığı sayısal değerleri betimlemek ya da özetlemek ise betimsel istatistik tekniklerini kullanmamız mümkündür. Araştırma amacımız, birden fazla değişken arasındaki ilişkiyi incelemek, değişkenlerin aldıkları değerleri karşılaştırmak, değişkenlerin birbirlerine olan etkilerini incelemek ya da evrene ait tahminler yapabilmek ise bu durumda yordamsal istatistik teknikleri uygulanmaktadır.

Betimsel istatistik , araştırma sonucu ortaya çıkan ham verilerin genel görünümünü veya özetini topluca görmeyi sağlar. Gündelik araştırmalar göz önüne alınırsa en çok kullanılan istatistik tekniğinin bu olduğunu söylemek mümkündür. Betimsel istatistik teknikleri yardımı ile dağılımın geneli hakkında özet bilgiler elde etmek ya da dağılımın kendi içindeki durumu hakkında bilgiler elde etmek mümkündür. Dağılım, her bir birimin ya da birim kümelerinin yinelemelerinin özetini verir. Bu dağılıma frekans dağılımı denir. Frekans dağılımı ile verilerin özetlenmesi anlaşılır bir biçimde sunulması mümkündür. Dağılım yüzde olarak verilirse bu dağılıma yüzde dağılımı ismi verilir. Birim sayısının fazla olduğu çalışmalarda yüzde dağılımını kullanmak daha uygun olacaktır.

Araştırma sonucunda elde edilen verileri kolay anlaşılır bir şekilde sunmanın diğer bir yolu da grafik yardımı ile gösterimdir. Farklı şekillerde düzenlenen grafikler mevcuttur. En sık kullanılanları; Çizgi Grafik, Sütun Grafik ve Pasta veya Halka Grafiktir, Dal-Yaprak Grafiği ve Histogramdır. Excel gibi bilgisayar programları sayesinde bu grafikleri hazırlamak oldukça kolaydır.

Çizgi grafikler , ortak bir ölçeğe göre ayarlanmış, zaman içindeki sürekli verileri görüntüleyebilir ve bu nedenle eşit aralıklarla veya zaman içinde verilerdeki eğilimleri göstermek için uygun olan grafiklerdir. İki eksen üzerinde verilerin çizgi olarak gösterilmesi ile oluşturulur.

Sütun grafikler , bir veya daha fazla veri kategorisini görselleştirmek için özellikle de her kategorinin alt kategorileri varsa iyi bir yöntemdir. Bu grafikler, her bir kategorinin veri noktaları arasındaki farkı görsel olarak ifade etmenize olanak sağlar. Sütun grafiği süreksiz değişkenleri özetlemek için uygun bir grafik şeklidir.

Pasta grafikler , veriler az şıklı olduğunda tercih edilen en çekici grafik türüdür. Bir bütünün parçalarının nasıl dağıldığı hakkında fikir verir. Verilerin tek değişkenli olması gerekir.

Dal-Yaprak grafikler , sayısal verilerin görsel hâlde sunumunda kullanılır. Tek değişkenli veriler için uygundur. Bu gösterim şekli veri setinin yapısını, örüntüsünü veya genel eğilimini gösterir. Grafikte yer alan satırlara “dal”, satırların yanındaki açıklamalara “yaprak” denir. Bu grafiği çizerken ve okurken kafamızda dallanmış bir ağaç görüntüsü oluşmaktadır.

Histogram , gruplandırılmış bir veri dağılımının sütun grafiğiyle gösterimine denir. Histogram sürekli değişkenler olduğunda, sütun grafik ise süreksiz değişkenler için kullanılmaktadır.

Merkezi Dağılım Ölçüleri

Dağılım, her bir birimin veya birim kümelerinin frekanslarının özetini verir. Grafikler veriler hakkında görsel sunumlar sağlamasına rağmen verinin dağılımı hakkında yeterli bilgiyi sunmazlar. Topladığınız verilerin özelliklerini ortaya koyacak değerlere ihtiyacınız vardır. Bir dağılım hakkında bilgi veren sayısal değerlere ihtiyacınız vardır. Bu değerler merkezî dağılım ölçüleri olarak isimlendirilirler. Merkezî dağılım ölçüleri tepedeğer, ortanca ve aritmetik ortalama olarak adlandırılır. Merkezî eğilim ölçüleri serinin özelliklerini gösteren tek bir değer bulunmasını ve bulunan bu değerin, diğer serilerin değerleri ile karşılaştırılabilmesini sağlar.

Tepedeğer bir seride en çok tekrarlanan yani frekansı en büyük olan değerdir. Diğer ortalamalardan farkı, hem nitel hem de nicel değişkenler için kullanılabilmesidir. Hatta sınışama ölçeği ile ölçülmüş veriler için kullanılan tek temsili değerdir. Süreksiz değişkenleri özetlemek için ideal bir değerdir. Sürekli değişkenler için temsiliyeti zayıftır. Önemli bir özelliği de serideki aşırı değerlerden etkilenmemesidir. Çünkü tepedeğer bulunurken serinin en yüksek frekanslı değeri dikkate alınır. Bir seride mod olmayabilir. Ya da bir seride birden fazla mod değeri olabilir.

Ortanca , sıralanmış bir serinin ortasındaki değerdir. Ortancayı bulmak için değerlerin belirli bir özelliğe göre sıraya dizilmesi gerekir. Bu nedenle ortancanın kullanılabilmesi için verilerin sıralama, eşit aralıklı ya da oranlı ölçekle ölçülmüş olması gerekir. Ortanca ortadaki değer olması nedeni ile seriyi iki eşit parçaya böler. Ortanca serinin ortasındaki değerle ilgilendiği için başta ve sonda yer alan aşırı değerlerden etkilenmez.

Tepedeğer ve ortanca seride yer alan bütün değerleri dikkate almadan hesaplanan ortalamalardır. Bu nedenle hassas olmayan ortalamalar olarak da isimlendirildikleri olur. Seride yer alan bütün gözlemleri dikkate almadıkları için, seriyi temsil edebilecek daha güçlü bir değere ihtiyaç vardır. Bu da aritmetik ortalamadır.

Aritmetik ortalama , bütün gözlemlerin toplamının gözlem sayısına bölümü ile elde edilir. Gözlem değerlerinin tamamını dikkate aldığı için daha tutarlıdır ve en çok kullanılan merkezi eğilim ölçüsüdür.

Bir seride uygun olmayan bir ortalama hesaplanması yarardan çok zarar getirir. Yorum buna göre yapıldığında yanlış bilgilendirme söz konusudur. Ortalamaların temsil gücünü etkileyen en önemli unsur hesaplandıkları serinin homojen olup olmamasıdır. Homojenlik azaldıkça uygun ortalama seçimi daha fazla önem kazanır.

• Seride aşırı değer, farklı işaretli değer, önemli tekrar sayısı farklılıkları yoksa Aritmetik Ortalama,
• Tekrar sayılarından biri diğerlerine göre farklı derecede büyükse veya nitel veri varsa Tepedeğer,
• Seride aşırı değerler varsa, açık seri söz konusu ise veya değerlerin sıraları önemli ise Ortanca en uygun ortalamadır.

Aritmetik Ortalama-Ortanca-Tepedeğer Arasındaki İlişki

Merkezî eğilim ölçülerini hesaplamanın amacı, bir değişkeni oluşturan değerleri tanımlamak ve gözlem değerlerinin nasıl dağıldığı anlayabilmektir. Dağılım şeklinin belirlenmesini merkezî eğilim ölçülerini birbirleri ile karşılaştırarak yapmak mümkündür. Bir dağılımın simetrik ya da çarpık olup olmadığı, ortalaması ile yakından ilgilidir. Bir dağılım simetrik ise merkezî eğilim ölçüleri birbirine eşit olur. Eğer bir dağılım asimetrik ise üç eğilim ölçüsü birbirinden farklı olur ve dağılımda çarpıklık var demektir.

Normal Dağılım: Tepedeğer, ortanca ve aritmetik ortalamanın birbirine eşit olduğu dağılıma normal dağılım denir. İstatistiksel olarak önemli bir dağılımdır. Normal dağılım, sürekli dağılım türlerinden biridir ve pratikte birçok durumda verilerin normal dağılım gösteren bir evrenden geldiği varsayılır. Bunun nedeni doğa ve insan davranışlarının genelinin normal dağılıma uygun olmasıdır. Normal dağılım çan eğrisi şeklinde ve simetrik bir dağılımdır.

Standart Normal Dağılım: Normal dağılımın parametrelerinin dağılımdan dağılıma değişeceği ve çeşitli olasılık değerleri için ileri matematiksel işlemlerin yapılması gerekmektedir. Bu da oldukça zordur. Bu güçlüğü gidermek için seri standartlaştırılır. Buna da standart normal dağılım denir. Değişkenlerin değerleri ortalaması 0 ve standart sapması 1’e eşit standart değişkene dönüştürülmektedir. Gözlem değerlerinin ortalamaya olan uzaklıklarının standart sapma cinsinden verilmesi ile Z puan denilen standart puan elde edilir. Z puanlarında ortalama değer 0’dır. Bu puanlar ile gözlem değerlerinin ortalamadan kaç standart sapma altında ya da üstünde olduğu hesaplanabilmektedir.

Değişkenlik Ölçüleri

Verilerin nasıl dağıldığı hakkında bilgi veren bir başka ölçü de değişkenlik ölçüleridir. Dağılımın çarpık olup olmadığı Merkezî Eğilim Ölçüleri ile belirlenirken, dağılımın sivri ya da yayvan oluşunu gösteren basıklığı belirlemek için değişkenlik ölçülerinden faydalanılır. Aritmetik ortalama dağılımın orta nokta noktasını gösteren bir ölçüdür. Ancak dağılımın yaygınlığı hakkında bilgi vermemektedir. Aslında istatistiğin konusu değişkenliktir. Değişkenlik olmasa istatistiğe gerek kalmazdı.

Veri gruplarındaki gözlem değerlerinin birbirlerinden ve ortalamadan ne ölçüde uzaklaştığını değişkenlik ölçüleri ile ölçebiliriz. Değişkenlik ölçülerinden en sık kullanılanları değişim aralığı, standart sapma ve değişim katsayısıdır.

Değişim Aralığı: En basit değişkenlik ölçüsüdür. Bir veri grubunda en büyük değer ile en küçük değer arasındaki farka değişim aralığı denir, R ile gösterilir. Değişim aralığının hesaplanmasında sadece iki uç değer işleme alındığından, diğer değerlerin hiçbir etkisi yoktur. Bu nedenle değişim aralığı yaygın olarak kullanılan bir değişkenlik ölçüsü değildir.

Standart Sapma: Dağılımdaki her bir değerin ortalamaya göre ne derece uzakta olduğunu, başka bir ifade ile dağılımın ne yaygınlıkta olduğunu gösteren bir ölçüdür. Bir dağılımda değerler ortalamadan uzaklaştıkça dağılımın yaygınlığı artar. Değişkenlik ölçüleri içinde matematiksel işlemlere en uygun ve en sık kullanılan değişkenlik ölçüsüdür. sapmanın önemli bir özelliği de aynı ölçekle ölçülmüş iki farklı dağılımın değişkenliğinin karşılaştırılmasında önemli bilgi sunmasıdır. Bu dağılımlardan hangisinin standart sapması daha küçük ise o dağılımdaki değişkenliğin daha az olduğu anlamına gelmektedir. O dağılımda veriler aritmetik ortalama etrafında daha çok toplanmaktadır. Daha homojen bir yapı söz konusudur.

Değişim Katsayısı: Değişkenlik ölçüleri içinde gözlem değerlerinin ölçü birimine bağımlı olmayan değişkenlik ölçüsü değişim katsayısıdır. Farklı ölçme birimleri ile ölçülmüş veri gruplarının değişkenliğinin karşılaştırılmasında ise değişim katsayısı kullanılır. Değişim katsayısı, x100 formülü ile hesaplanır. Değişim katsayısı % cinsinden ifade edilir. Değişim katsayısı küçük olan dağılımlarda değişkenlik daha azdır.

Yordamsal İstatistikler

Betimleyici istatistiklerde toplanan verinin dağılımı hakkındaki bilgilerin yanı sıra örneklem verileriyle evren hakkında bazı sonuçlara ulaşmak da hedeflenebilir. Bu durumda betimleyici istatistikler yetersiz kalacaktır. Daha fazla açıklayıcı bilgi alımı sağlayan yordamsal istatistikler yardımı ile

• Örneklem bilgilerine dayanarak evren değerlerini tahmin etme
• Bir ya da birden fazla değişken yardımı ile iki ya da daha fazla grup arasında bir fark olup olmadığını ortaya koymayı sağlama
• Değişkenler arasındaki sistematik ilişkiyi anlamak için kullanılan ve iki değişken arasındaki ilişkinin yönünü ve türünü inceleme
• Geçmiş verilere dayanarak gelecek hakkında tahmin yapabilmeyi gerçekleştirmek mümkündür.

Yordamsal istatistik kavramını tanımlayacak olursak değişkenler arasında saptanan ilişkilerden hareketle bir dağılımdaki durumdan başka bir dağılımdaki durumu tahmin etmeye, yordamaya, kestirmeye ya da öngörmeye olanak sağlayan istatistiksel tekniklerin tümüne yordamsal istatistik denmektedir. Yordamsal istatistikler, betimleyici istatistiklere göre daha karmaşık olup onları da kapsayan hesaplamalar içermektedir.

Hipotez Testleri

Hipotez, araştırılabilir bir olay, olgu veya fikri mantıklı ve bilimsel olarak açıklamaya yönelik yapılan tahmin olarak tanımlanır. Hipotez doğru ya da yanlış olabilir. Hipotezler doğrulanmak için değil sınanmak için ortaya atılırlar. Hipotez, bir beyandır. Belirli varsayımlara dayanmaktadır.

İstatistiksel hipotezlerin testinde iki tür hipotez söz konusudur. Bunlar; sıfır hipotezi ve karşı hipotezdir.

Sıfır Hipotezi ; H0 simgesi ile gösterilir ve test edilen hipotezdir. Hipotez testlerinin sonucunda ya H0 kabul edilecek ya da H0 ret edilecektir. H0 hipotezi, evren parametre değerleri hakkında iddia edilen önsavdır. H0 hipotezi, yokluk hipotezi, eşitlik hipotezi olarak da isimlendirilir. Örneklem değerleri ve evren değerleri arasındaki farkın örnekleme hatasından kaynaklanabileceğini, bu iki değer arasında gerçekte bir farkın bulunmadığını, bulunan farkın şans eseri olacağını savunur.

Karşı Hipotez ; Sıfır hipotezinin test edilmesi için ortaya atılan H1 simgesi ile gösterilen hipotezdir. Alternatif hipotez olarak da isimlendirilir. Örneklem değerleri ve evren değerleri arasında gerçekte bir fark olduğunu savunur.

İstatistiksel testlerde sıfır hipotezi ve karşı hipotezin istatistiksel semboller ile gösteriminin yapılması gereklidir. Araştırma konusu olan hipotezler hangi dilde yazılmış olursa olsun istatistiksel semboller ile yazıldıklarında herkes tarafından anlaşılabilir hale gelirler. Hipotezlerinin yazımında evrene ait parametre değerlerinin istatistiksel sembolleri kullanılır. Sıfır hipotezi genellikle eşitlik ile ifade edilir. Karşı hipotez ise üç farklı şekilde kurulabilir.

Hipotez Testinin Aşamaları

• Hipotezlerin oluşturulması
• Anlam düzeyinin belirlenmesi
• Örneklemden veri toplanması
• Kullanılacak dağılım türünün belirlenerek test istatistiğinin hesaplanması
• Hesaplanan test istatistiğinin, ölçüt olarak kabul edilen değer ile karşılaştırılması
• İstatistiksel kararın verilmesi biçimindedir.

İlk aşama olan hipotezlerin oluşturulmasında dikkat edilmesi gereken bazı önemli noktalar bulunmaktadır. Oluşturulacak hipotez cümlesi; test edilebilir, aksi ispatlanabilir, tahmin içerebilir bir yapıda olmalıdır. İyi bir hipotez cümlesi oluşturmak için açık, basit, öz ve kısa ifadeler kullanmak gerekir. Her hipotez cümlesi bir tek hipotez içermelidir. Hipotezlerin örneklemden veri toplamadan önce kurulması gerekir. Aksi hâlde örnekten elde edilen verilerin hem hipotezlerin kurulmasında hem de test edilmesinde kullanılması durumu ortaya çıkar.

Anlamlılık düzeyi, herhangi bir sonucun tesadüfi olarak ortaya çıkma olasılığını gösteren değerdir. ? simgesi ile gösterilir. Araştırmada elde edilen sonucun şans eseri gerçekleşme olasılığı olarak da ifade edilen anlamlılık düzeyi, sosyal bilimler için genellikle ?= 0,05, sağlık bilimleri için ?= 0,01 olarak alınmaktadır. Bunun sebebi, sağlık bilimlerinde araştırma sonucunda alınan kararların sonuçlarının daha ciddi durumlara sebep olma ihtimalidir.

Hipotez testlerinde örneklem verilerinin tesadüfi bir değişken olması nedeniyle iki çeşit hata yapılabilir. Bu hatalar I. Tip Hata ve II. Tip olarak isimlendirir.

I. Tip Hata ; kabul edilmesi gereken H0 hipotezi yanlış diye ret edildiğinde,

II. Tip Hata ; ret edilmesi gereken H0 hipotezi doğru diye kabul edildiğinde ortaya çıkar. Her iki durumda da karar hatalıdır.

İstatistiksel bir hipotezde ret bölgesinin büyüklüğü, hipotez testinde belirlenen ? değerine bağlıdır. “?” değeri hipotez testine başlamadan önce araştırmacı tarafından belirlenir. I. Tip hata ve II. Tip hata matematiksel olarak hesaplanabilir. “Güven Düzeyi”, ise “Testin Gücü” olarak adlandırılır.

Araştırmacı, hipotez testini gerçekleştirirken anlamlılık düzeyini 0.05 olarak seçerse doğru bir sıfır hipotezini reddetme, yani I. tip hata yapma olasılığı %5’tir. Anlamlılık düzeyini 0.001 olarak seçtiği zaman bu tip hataya düşme olasılığı binde bire düşer ancak böyle bir durumda da yanlış olan bir sıfır hipotezini reddedememe olasılığı, yani II. Tip hata ihtimali artmaktadır. Bir başka deyişle aslında anlamlı olan bir sonucu görememe tehlikesi doğmaktadır. Bu bağlamda iki hatanın birbiriyle doğrudan ilişkili olduğu dikkate alınmalı, bir hatadan kaçınmaya çok önem vermenin öbür hatayı gerçekleştirme olasılığını arttırdığı gözden kaçırılmamalıdır. Bilimsel çalışmalarda I. tip hatadan kaçınmaya daha çok ağırlık verilmekte bu nedenle 0.05’in altında belirlenmiş 0.01 gibi anlamlılık değerlerine sıklıkla rastlanmaktadır. Sosyal bilimlerde yapılan istatistiksel testlerde 0.05 ve altında anlamlılık değerleri görüldüğü zaman istatistiksel olarak anlamlı bir fark bulunduğu sonucuna varılmaktadır. Anlamlılık değeri birçok programda ve araştırma raporunda p harfi ile gösterilir.

p<0.05 denildiği zaman sonuçların istatistiksel olarak anlamlı, p>0.05 denildiği zaman ise sonuçların anlamsız olduğu anlaşılmaktadır.

Doğrudan p değerleri verildiği zaman ise 0.05 ve altındaki değerler anlamlı, 0.05 üzerindeki değerler anlamsız kabul edilecektir.

Yordamsal İstatistik Çeşitleri

t-Testi: Genellikle hipotez testlerinde en yaygın olarak kullanılan yöntemdir. t testi ile iki grubun ortalamaları karşılaştırılarak, aradaki farkın tesadüfi mi yoksa istatistiksel olarak anlamlı mı olduğuna karar verilir. t testi, küçük örnekleme teorisi olarak da bilinen t dağılımı varsayımı altında çalıştığı için, küçük örneklemlerle de çalışmaya uygundur. Araştırmacılar açısından bu yönüyle avantajlı bulunur.

t testinde serbestlik derecesi kavramı bulunmaktadır. Serbestlik derecesi, bir serideki serbestçe değişebilecek terim sayısını gösterir.

Üç tür t testi bulunmaktadır. Bunlar; tek grup t testi, bağımsız iki grup arası farkların t testi ve eşleştirilmiş iki grup arasındaki farklılıkların incelenmesine yönelik t testidir.

• Tek grup t Testi : Gözlenen bir değişken açısından bir gruba ait ortalama değerin önceden belirlenen değerden farklı olup olmadığını inceler. Bu test genellikle herhangi bir konuda belirli öngörülerde bulunulduğunda bu öngörünün doğruluk derecesini test etmek amacıyla uygulanır.
• Bağımsız iki grup arası farkların testi : Gözlenen bir değişken açısından bağımsız iki grup arasında fark olup olmadığını inceler. Burada dikkat edilmesi gereken nokta grupların birbirinden bağımsız olması gerektiğidir. Genellikle araştırmalarda farklı grupların karşılaştırılmasına yönelik hipotez testleri yapılır. Bu test bu amaca hizmet etmektedir.
• Eşleştirilmiş iki grup arasındaki farkların testi : Gözlenen bir değişken açısından herhangi bir grubun farklı koşullar altındaki tepkilerinde farklılığın olup olmadığını inceler. Özellikle deneysel çalışmalarda aynı deneklerin farklı durumlarda nasıl davrandıklarının incelenmesine gerek duyulabilir. Burada amaç, farklı iki koşulda elde edilen sonuçların farklı olup olmadığını araştırmaktır. Eşleştirilmiş iki grup arasındaki farkların tespitini üç farklı yapı için yapmak mümkündür;

Bir grubun iki bağımlı değişkene ilişkin ortalamalarının karşılaştırılarak, ortalamalar arasındaki farkın anlamlı olup olmadığını belirlemek.

İkinci olarak ön test-son test olarak adlandırılabilecek bir yapıdır. Burada bir örneklemin tek bir değişkene ilişkin iki farklı zamandaki ölçümlerine ait ortalamaların karşılaştırılması yapılabilir.

Üçüncü olarak, sağlık ve fen bilimleri alanlarında daha fazla karşılaşılan bir durum söz konusudur. Bazen araştırmayı aynı örneklem ya da denek grubuna uygulamak mümkün olmayabilir. Bu durumda benzer özelliklere sahip farklı örneklem kullanılabilir. Burada iki grubun eşleştirilmesi, ölçüm sürecinden önce iki grup arasında ölçüm yapılacak konuda fark olmadığını varsaymak anlamına gelmektedir.

t testi için dikkat edilmesi gereken nokta 2 sayısıdır. t testinin kullanılabilmesi için 2 grup söz konusu olmalıdır. t testlerinin hepsi 2 grup ortalamasını karşılaştırır. 2’den fazla grup varsa t testi uygulanamaz. Grup sayısı 2’den fazla ise t testi yetersiz kalır ve varyans analizi uygulanır.

Varyans Analizi: Yapılan çalışmalarda grup sayısı ikiden fazla olduğunda t testi yetersiz kalmakta, grupların ortalamalarının ikili karşılaştırmalarını yaparken I. Tip hata yapma olasılığını arttırmaktadır. Bu nedenle 2’den fazla grup söz konusunu ise bu durumda tek yönlü varyans analizi kullanılmalıdır. Varyans analizine F testi ismi de verilmektedir. Bunun nedeni varyans analizinin F dağılımı varsayımı altında çalışmasıdır. İstatistiksel bilgisayar programlarında ise ANOVA olarak geçer. Varyans Analizi, sonuca etkide bulunma bakımından değişkenler arasında fark olup olmadığının incelenmesini sağlar. t testi gibi sadece 2 grup ortalamasının karşılaştırılması gibi herhangi bir sınırlaması yoktur. Bağımsız değişkenlerin sayısı da istenildiği kadar arttırılabilir. Araştırmada tek bağımsız değişken varsa tek yönlü, iki değişken varsa iki yönlü, üç değişken varsa üç yönlü, dört ve daha çok değişken varsa çok yönlü varyans analizi yapılmaktadır.

Varyans analizinin yapılabilmesi için, karşılaştırılacak grupların birbirinden bağımsız olması ve bu gruplardan elde edilmiş verilerin en az aralıklı ölçek ile ölçülmüş olması gerekir. Varyans analizinde hipotez şu şekilde ifade edilir;

H0 : Her grubun ilgili değişken için ortalaması eşittir.

H1 : Gruplardan en az birinin ortalaması diğerlerinden farklıdır.

Varyans analizinde iki serbestlik değercesi bulunmaktadır. İlki karşılaştırılan grup sayısından 1 çıkartılarak bulunur. İkinci serbestlik derecesi ise toplam katılımcı sayısından karşılaştırılacak grup sayısının çıkartılması ile bulunur. t testinde olduğu gibi burada da p<0,05 ise gruplar arasında istatistiksel olarak anlamlı bir fark olduğu söylenir. Hangi grup ya da grupların farklılaştığını görmek için ikili karşılaştırmalar yapılır.

Korelasyon: Değişkenlerin bağımlı ya da bağımsız olmasını dikkate almaksızın, değişkenler arasındaki ilişkinin yönü ve derecesini belirten istatistiksel yöntemdir. Korelasyon değişkenler arasındaki sebepsonuç ilişkilerini açıklamaz. İki değişkenin birbirlerini ne kadar açıkladığını gösterebilir ama hangi değişkenin hangi değişkeni etkilediği hakkında bilgi vermez.

Pearson korelasyon katsayısı, en az aralıklı ölçekle ölçülmüş olan değişkenlerin arasındaki doğrusal ilişkinin derecesine ve yönüne bakmak istenildiğinde en sık kullanılan katsayıdır. “r” simgesi ile gösterilir. Korelasyon katsayısı -1 ile +1 değerleri arasında yer değişen değerler alır. Korelasyon katsayısının eksi değerler alması değişkenler arasındaki ilişkinin ters orantılı olduğunu, artı değerler alması değişkenler arasındaki ilişkinin doğru orantılı olduğunu gösterir. r değeri ±1 ‘e yaklaştıkça ilişkinin kuvveti artarken 0’a yaklaşması ilişkinin kuvvetinin az olduğunu gösterir. Korelasyon katsayısının yorumunda r değeri tam değerler dışında ara değerler aldıysa yorum yapmak güçleşmektedir. Kesin sınırlamalar olmamakla birlikte 0,50’nin altındaki korelasyon zayıf, 0,50-0,70 arasındaki korelasyon orta ve 0,70’in üzeri korelasyon da kuvvetli ilişki gösterecektir.

Korelasyon katsayıları örneklem büyüklüğünden etkilenmektedir. Oysa r değerlerinin istatistiksel olarak anlamlı çıkması, bu değerlerin pratikte de çok önemli olduğu anlamına gelmez. Bu nedenle r değerinin karesi alınarak iki değişken arasındaki ortak alanın büyüklüğü hakkında yorum yapmak en doğrusudur. r değerinin karesini alarak bulduğumuz bu değere belirleme katsayısı adı verilir.

Ki-Kare Testi: Sürekli değişkenlerin varlığında t ve F testleri kullanılırken süreksiz değişkenlerde bu testlerin kullanılması mümkün değildir. Bu durumda parametrik olmayan bir test olan Ki- Kare testi kullanılır. ?2 simgesi ile gösterilir. Ki- Kare testi iki süreksiz değişken arasındaki ilişkinin belirlenmesinde kullanılır. Nitel değişenler için kullanılabiliyor olması nedeniyle sosyal bilimler araştırmacılarının kullanmayı tercih ettikleri bir tekniktir. Üç farklı yapıda kullanılabilir. Bunlar; Ki-Kare Bağımsızlık Testi, Ki-Kare Homojenlik Testi ve Ki-Kare Uygunluk Testi biçimindedir.

• Ki-Kare Bağımsızlık Testi: Bu testte değişkenler arasında bağımlılık olup olmadığına bakılır. Bu testte serbestlik derecesi (satır sayısı-1). (sütun sayısı-1) ile bulunur. Hipotezleri şu şekildedir;
  H0 : İki değişken arasında bağımsızlık vardır.
  H1 : İki değişken arasında bağımsızlık yoktur .
  Bu test özünde gözlem değerlerinin beklenen değerlerden farklı olup olmadığını test eder.
• Ki-Kare Homojenlik Testi : Benzer nedenlerin ve olayların etkileri bakımından homojen olup olmadıklarını gözlem değerleri ile beklenen değerler arasındaki farkın anlamlı olup olmadığını, bu farkların örnekleme hatalarından kaynaklanıp kaynaklanmadığını test eder. Bu testte serbestlik derecesi (satır sayısı-1).(sütun sayısı-1) ile bulunur. Hipotezleri şu şekildedir;
  H0 : İki değişken arasında homojenlik vardır
  H1 : İki değişken arasında homojenlik yoktur.
• Ki-Kare Uygunluk Testi : Burada gözlenen frekansların beklenen frekanslara uyup uymadığı araştırılır. Gözlenen frekanslardan oluşan dağılım ile beklenen frekanslardan oluşan dağılım arasındaki farkın tesadüfi sebeplerden mi yoksa anlamlı bir fark yarattığından mı olup olmadığı incelenir. Bu testte serbestlik derecesi (sınıf sayısı-1) ile bulunur. Hipotezleri şu şekildedir;
  H0 : Uygunluk vardır
  H1 : Uygunluk yoktur.