Devre Analizi Dersi 8. Ünite Özet

Giriş

Alternatif akım devreleri, kullanılan devre elemanlarının frekans değişiminden etkilenmesinden dolayı, zaman düzlemi yerine frekans düzleminde analiz edilir. Fakat devrelerin frekans düzleminde analiz edilmesi, doğru akım devrelerindeki analiz yöntemlerinin bu devreler için de kullanılmasını engellemez.

AA devrelerinde kullanılabilecek analiz yöntemleri Kirchhoff yasaları, düğüm noktası yöntemi, çevre akımı yöntemi, süperpozisyon yöntemi, güç dönüşümü yöntemi ve Thevenin ve Norton teoremlerinin tamamını kapsar.

AA devrelerinde önemli kavramlardan biri rezonanstır. Rezonans, devrenin belirli bir frekansta girdiği özel bir durumdur. Rezonans frekansında devredeki güç kazancı en büyüktür. AA devrelerinde diğer önemli husus güç hesaplamalarıdır. Güç hesaplamalarında anlık güç, ortalama güç, reaktif güç, kompleks güç ve görünür güç kavramları ile karşılaşılır.

AA devrelerinin güç hesaplamalarında bir diğer kavram olan güç faktörü, ortalama güç ve reaktif güç arasındaki ilişkiyi anlatmaktadır. Kaliteli bir güç iletiminde reaktif güç istenilmeyen bir bileşen olduğundan güç kalitesini arttırmak için güç faktörü üzerinde istenilen kısıtlamalar doğrultusunda düzeltmeler yapılması gerekmektedir.

Doğru Akım Analiz Yöntemlerinin Alternatif Akım Devrelerine Uyarlanması

AA devrelerinin analizinde, devre zaman düzleminden kompleks sayı düzlemine fazörler yardımıyla aktarılır. Akım veya gerilim kaynakları kutupsal veya kartezyen gösterimle ifade edilen fazörlere çevrilir. Kondansatör, bobin ve direnç gibi devre elemanlarının uygulanan frekansa bağlı fazörlerle ifade edilen empedans karşılıkları hesaplanır. Bütün elemanlar için fazör dönüşümü yapıldıktan sonra uygun analiz yöntemi seçilir.

Kirchhoff Yasalarının Kullanımı

Kirchhoff gerilim yasası ve Kirchhoff akım yasası olmak üzere iki temel Kirchhoff yasası vardır. Kirchhoff gerilim yasasına göre kapalı bir yol üzerindeki gerilimlerin cebirsel toplamı sıfırdır. Kirchhoff akım yasasına göre bir düğüm noktasına giren veya düğüm noktasından çıkan akımların cebirsel toplamı sıfırdır.

Bu iki kural frekans düzleminde de geçerlidir. Frekans düzleminde farklı olarak toplamı hesaplanacak gerilimler veya toplamı hesaplanacak akımlar kompleks sayılarla ifade edilir. Dolayısıyla sıfıra eşitleme yaparken hem gerçek hem de sanal kısımların toplamı kendi içinde 0’a eşit olmalıdır. Kirchhoff yasasına göre;

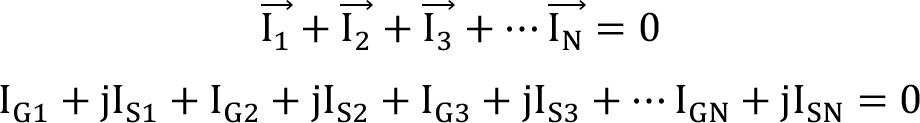
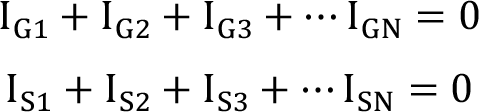
G indisiyle belirtilen ilgili akımın gerçek bileşeni, S indisiyle belirtilen ilgili akımın sanal bileşenidir.

Düğüm Noktası Yönteminin Kullanımı

Düğüm noktası yöntemi Kirchhoff akım yasasının bir uygulamasıdır. Seçilen düğüm noktaları kullanılarak akım denklemleri oluşturulur.

Çevre Akımı Yönteminin Kullanımı

Çevre akımı yöntemi Kirchhoff gerilim yasasının bir uygulamasıdır. Seçilen çevre akımları kullanılarak gerilim denklemleri oluşturulur.

Süperpozisyon Yönteminin Kullanımı

Devrede birden fazla bağımsız kaynak varsa ve bu kaynakların frekansları birbirinden farklı ise, devre fazörler kullanılarak ancak süperpozisyon yöntemiyle çözülür.

Bu yöntemde, devrede her aşamada bir kaynak yalnız bırakılır ve diğer kaynaklar öldürülür. Bulunmak istenilen değişken, fazör ortamında bulunur. Elde edilen sonuç zaman düzlemine çevrilir.

Tüm kaynaklar için ilgili değişken (akım, gerilim vb.) zaman düzleminde ayrı ayrı bulunduktan sonra elde edilen sonuçlar yine zaman düzleminde toplanır.

Kaynak Dönüşümü Yönteminin Kullanımı

Devrenin analizini kolaylaştırmak için DA devrelerinde kullanılan kaynak dönüşümü yöntemi AA devrelerinde de kullanılabilir. Bu yöntemde gerilim kaynağına seri bağlı yük (empedans), akım kaynağına paralel bağlı yük şekline dönüştürülebileceği gibi tam tersi de söz konusudur (S:199, Şekil 8.13).

Thevenin veya Norton Eşdeğerlerinin Kullanımı

Bir devredeki herhangi bir elemanın üzerine düşen akım veya gerilimin hesabında Thevenin veya Norton eşdeğerlerinin kullanımı için sırasıyla şu işlemler uygulanır:

• Devre elemanı açık devre yapılarak devreden çıkarılır.
• Açık devre yapılan uçlar arasındaki eşdeğer empedans bağımsız kaynaklar öldürülerek hesaplanır. Hesaplanan empedans Thevenin Empedansı ( 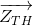)’dır.(Thevenin) Açık uçlar arasında hesaplanan açık devre gerilimi Thevenin Gerilimi ( 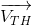)’dır.
• (Norton) Açık uçlar kısa devre yapılarak kısa devre akımı hesaplanır. Bu Norton Akımı ( 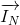)’dir.
• Elde edilen eşdeğer devrenin açık uçlarına çıkartılan devre elemanı bağlanarak sadeleştirilmiş devre üzerinde istenen akım veya gerilim bulunur.

Bir devrenin Thevenin eşdeğeri ile Norton eşdeğeri arasında kaynak dönüşümü yöntemindeki gerilim kaynağıakım kaynağı denkliği vardır. Bir başka deyişle Thevenin eşdeğeri kaynak dönüşümü kullanılarak Norton eşdeğerine, Norton eşdeğeride aynı şekilde kaynak dönüşümü kullanılarak Thevenin eşdeğerine çevrilir.

Rezonans

İçinde en az bir bobin ve bir kondansatör bulunduran devrelerde rezonans kavramından bahsedilir. Rezonans durumu belirli bir frekansta gerçekleşir ve rezonans durumunda endüktif ve kapasitif reaktanslar birbirini dengeleyerek reaktans sıfıra eşitlenir. Bu noktada devrenin eşdeğer empedansı direnç gibi davranır ve devrenin üzerinden geçen akım ile devrenin eşdeğer gerilimi arasındaki faz farkı sıfırdır.

Seri RLC Devreleri İçin Rezonans

Seri RLC devrelerinde (S:204, Şekil 8.23) eşdeğer empedans direncin, kondansatörün ve bobinin empedansları toplamıdır. Rezonans frekansında kondansatör ve bobin reaktansları birbirine eşittir.

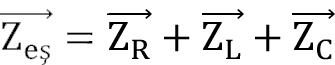
Rezonans frekansı w ₀ :

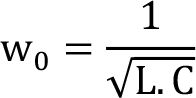
Frekans, rezonans frekansından büyük ise eşdeğer reaktans endüktif, küçük ise kapasitif özellik göstermektedir.

Paralel RLC Devreleri İçin Rezonans

Paralel RLC devrelerinde (S:205, Şekil 8.25) eşdeğer admitans, direncin, kondansatörün ve bobinin admitansları toplamıdır. Rezonans frekansına ulaşabilmek için kondansatör ve bobinden kaynaklanan sanal iletkenliğin 0’a eşit olması gerekmektedir.

Frekans, rezonans frekansından büyük olduğunda eşdeğer reaktans kapasitif, küçük olduğunda endüktif özellik gösterir.

Alternatif Akım Devrelerinde Güç Hesaplamaları

AA devrelerinde akım ve gerilim zamana bağlı değişken olduğu için birim zamanda harcanan güç de değişim gösterir. Bu yüzden AA devrelerinde güç zamana bağlı bir fonksiyondur. Akım ve gerilim arasındaki faz farkından dolayı güç hesaplamaları da fazör ile yapılmaktadır.

Hem karmaşık sayılarla yapılan işlemlerden hem de zamana bağlı değişimden dolayı birden fazla güç kavramı söz konusudur.

Anlık Güç

Güç, sinüzoidal fonksiyon özelliği gösteren AA akım ve gerilimlerde de akım ile gerilimin çarpımına eşittir.

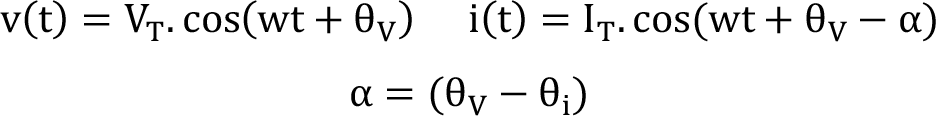
Anlık güç:

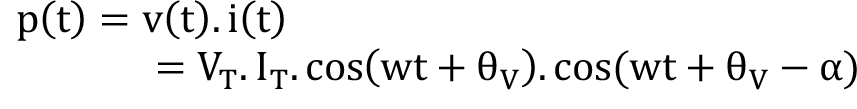
? gerilim ile akım arasındaki faz farkıdır. Akımın gerilimden ne kadar önde veya ne kadar geride olduğunu göstermektedir. Pozitif ise gerilimi takip etmekte, negatif ise gerilimden önde gitmektedir.

p(t) düzenlenerek elde edilen eşitlik:

Ortalama Güç

Sinüzoidal akım ve gerilimlere sahip devrelerin anlık gücü de sinüzoidal ve dolayısıyla da periyodiktir. Bu nedenle AA akım ve gerilimlerin ortalama değerinin hesabı ile ortalama gücün hesaplanması aynıdır

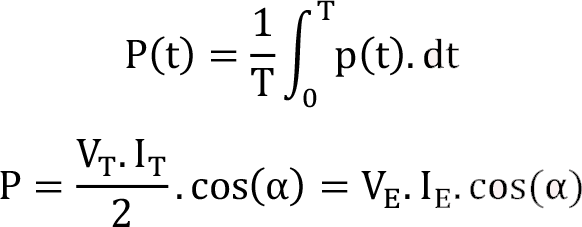
Direnç üzerindeki ortalama güç hesabında, dirençten kaynaklanan faz farkı 0º olduğundan ortalama güç:

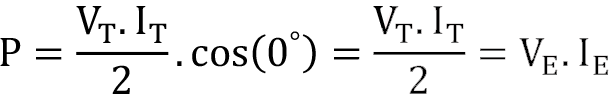
Kondansatörden kaynaklanan faz farkı -90º olduğundan kondansatör üzerindeki ortalama güç:

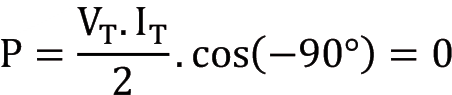
Bobinden kaynaklanan faz farkı 90º olduğundan bobin üzerindeki ortalama güç:

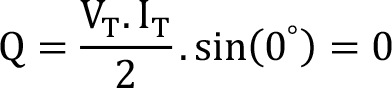
Reaktif Güç

Ortalama güç, devre empedansının direnç bileşeni üzerinde oluşan güçtür. Ayrıca devrenin empedansının reaktans bileşeninden dolayı açığa çıkan bir kayıp güç söz konusudur. Bu kayıp güç reaktif güç olarak adlandırılır. Q ile gösterilir.

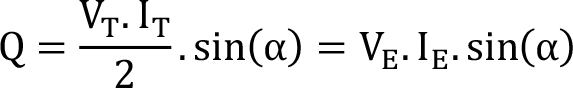
Reaktif gücün birimi VAR (Volt Amper Reaktif)’dır.

Direnç üzerindeki reaktif güç (faz farkı 0º):

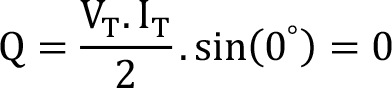
Kondansatör üzerindeki reaktif güç (faz farkı -90º):

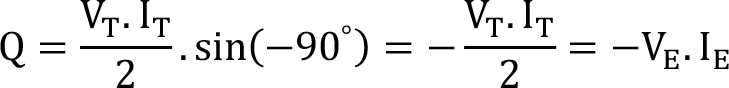
Bobin üzerindeki reaktif güç (faz farkı 90º):

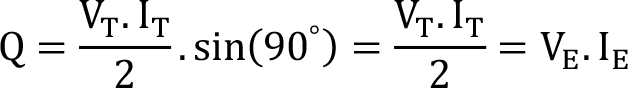
Kompleks Güç

Ortalama güç ve reaktif gücü aynı anda gösteren karmaşık (kompleks) sayılı vektörel güç ifadesine kompleks güç adı verilir. S ile gösterilir.

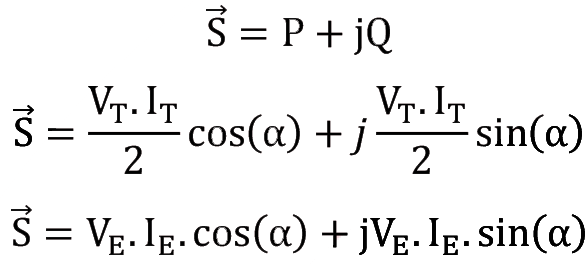
Karmaşık gücün birimi VA (Volt Amper)’dir.

Görünür Güç

Kompleks gücün mutlak değeridir

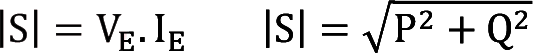
Görünür gücün birimi VA (Volt Amper)’dir.

Güç Faktörü

Ortalama gücün görünür güce olan oranıdır. PF ile gösterilir.

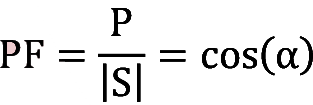
Güç faktörü pozitif olarak verilir. Nümerik değer, faz açısının pozitif veya negatif olup olmadığı hakkında bilgi vermemektedir. Bunun için PF’nin yanına pozitif faz açısı için geri (veya endüktif) , negatif faz açısı için ileri (veya kapasitif) ifadesi kullanılır.

Endüktif veya geri güç faktörüne sahip devre elemanının eşdeğer reaktansı bobin, kapasitif veya ileri güç faktörüne sahip devre elemanının eşdeğer reaktansı kondansatör davranışı gösterir. Güç faktörünün büyük olması güç kalitesi adına tercih edilen bir durumdur.

Güç faktörü büyüdükçe reaktif güç yani kayıp güç azalır.

Endüktif (geri) PF için faz açısı:

? = arc cos(PF)

Kapasitif (ileri) PF için faz açısı:

? = -arc cos(PF)

Güç Faktörünün Düzeltilmesi

Güç faktörünün düzeltilmesindeki amaç devreye uygun ilave elektriksel yükü bağlayarak devrenin harcadığı reaktif yani kayıp gücü azaltmak, diğer bir deyişle güç faktörünü yükseltmektir.

Bu tür düzeltmelerde izlenilecek yol şu şekildedir:

1. Mevcut devrenin harcadığı ortalama güç ve reaktif güç hesaplanır.
2. İstenilen güç faktörünün sağlanması için harcanması gereken reaktif güç hesaplanır.
3. Harcanması gereken reaktif güçten mevcut reaktif güç çıkarılır. Elde edilen güç devreye eklenecek elemanın harcayacağı reaktif güçtür.
4. 3. maddede hesaplanan fark negatifse bağlanacak olan yük kondansatör, pozitifse bağlanacak yük bobindir.
5. İlave yük devreye paralel bağlanacaksa üzerine düşen gereken gerilim, seri bağlanacaksa üzerinden geçen akım kullanılarak ilave yükün reaktansı hesaplanır.
6. Devrenin çalışma frekansı kullanılarak ilave yükün değeri reaktans kullanılarak bulunur.