Teknolojinin Bilimsel İlkeleri Dersi 4. Ünite Özet

Giriş

Belirli bir şekli olmayan ve bulunduğu kabın şeklini alan sıvı ve gaz halindeki maddelere akışkan adı verilir. Akışkanları katılardan ayıran en önemli özelliği, akışkanı oluşturan moleküllerin bağlarının katı haldeki moleküllerin bağlarına göre daha zayıf olmasıdır. Bilindiği üzere moleküller, atomların belirli kurallara göre bir araya gelerek oluşturdukları, maddenin özelliklerini taşıyan en küçük yapılardır. Gazlar daha kolay sıkıştırılabilen akışkanlardır. Sıvılar ise çok sıkıştırılamazlar ancak şekilleri değiştirilebilir.

Öz Kütle, Yoğunluk ve Basınç

Akışkanlar incelenirken, kütlesi yerine çoğunlukla yoğunluğu alınır. Bir cismin birim hacminin kütlesine o cismin yoğunluğu (p) adı verilir:

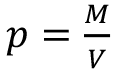eşitliğinde M kütle, V ise hacmi ifade eder. SI birim sisteminde kütlenin birimi kg, hacim ise m3 ile ifade edilebileceğinden yoğunluğun birimi ise kg/m3 ’tür. Bazı problem çözümlerinde yoğunluk için g/cm3 cinsinden gösterimler de kullanılabilir

Yoğunlukları p ₁ ve p ₂ olan iki sıvı karıştırıldığında ise, bu karışımın yoğunluğu;

eşitliğiyle bulunur.

Farklı yoğunluktaki birbiriyle karışmayan akışkanlar bir kaba konulduğunda, yoğunlukları büyükten küçüğe olacak şekilde aşağıdan yukarıya doğru sıralanır. En yukarıda en düşük yoğunluklu akışkan yer alır.

Durgun Bir Sıvı İçindeki Basınç

Akışkanlar konusundaki önemli kavramlardan birisi de basınçtır. Birim yüzeye dik olarak etki eden kuvvete basınç adı verilir. Yüzey alanın büyüklüğü A , dik olarak bu yüzeye etkiyen kuvvet F olmak üzere, basınç ( P );

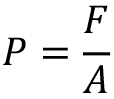
eşitliği ile hesaplanır. SI birim sisteminde basınç birimi N/m2 ’dir. Bu birime Pascal ( Pa ) da denir.

Yoğunluğu p taban alanı A ve yüksekliği h olan bir sıvının tabanına yaptığı basınç hesaplanabilir. Bu sıvının hacmi;

V = A. h

şeklindedir. Sözü edilen sıvının kütlesi ise M = p.V ; olduğundan, M = p.A.h yazılabilir. Sıvının tabanına uyguladığı kuvvet ise kendi ağırlığı kadar olduğundan

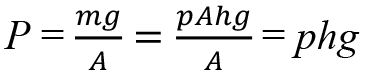
bulunur.

Açık Hava Basıncı

Hava da bir akışkan olduğundan onun da bir basıncı vardır. Açık hava basıncı konusunda ilk deneyleri Torricelli yapmıştır. Deniz seviyesinde cıva kullanarak yaptığı ölçümlerde açık hava basıncını 76 cmHg bulmuştur. Bunun anlamı, açık hava basıncı (Sf. 98, Şekil 4.1), boru içerisindeki cıvayı 76 cm yüksekliğe kadar bir kuvvetle itmektedir.

Pascal Prensibi

Pascal, Torricelli’ nin çalışmalarından hareketle sıvıların denge problemi ve açık hava basıncı hakkında çalışmalar yapmıştır. Blaise Pascal aynı zamanda yazar ve matematikçidir. İlk hesap makinesi projesini hazırlamış ve olasılık teorisi üzerine çalışmalar yapmıştır. Pascal sıvıların basıncı iletmesi konusunda ise “Kapalı bir kapta bulunan bir sıvıya dışardan yapılan basınç, sıvı tarafından bu sıvının her noktasına ve kabın çeperlerine aynen iletilir” ifadesini kullanmıştır. Bu ifade Pascal yasası olarak bilinir.

Pascal Yasası, durgun akışkanlar için geçerlidir ve durgun akışkanlarda akışkan basıncının yüksekliğe olan bağlılığından yararlanır. Bu önemli bağıntı hidrolik presler, hidrolik krikolar gibi uygulamalarda iş yapmak için, birim hacim başına enerji ölçüsü olarak durgun sıvının basıncından yararlanmak için kullanılabilir. Bu durumu bir örnekle açıklayalım:

Örn: Bir otomobil tamirhanesinde su cenderesi ile çalışan sistemde otomobiller yükseğe kaldırılarak tamir edilmektedir. Otomobilin konduğu kaldırma tablasının altındaki pistonun alanı A ₁ =1 m ² , kuvvet uygulanan kolun altındaki pistonun alanı ise A ₂ =0,2 m ² dir. 1,5 ton kütleli bir otomobili kaldırmak için sisteme uygulanması gereken en az kuvvet kaç N’ dur?

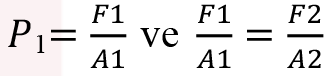eşitlikleri kullanılarak;

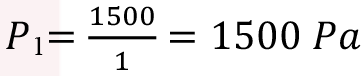bulunur. Kuvvet uygulanacak piston içinde basınç değerinin en az 1500 Pa olması gerekir.

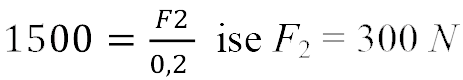bulunur.

Archimedes Prensibi

Günlük yaşamın içinde akışkanların bazı etkilerini sıklıkla görürüz. Havada uçan bir balon, yüzen gemi gibi. Tüm bunların olmasının nedeni akışkanın cisim üzerine uyguladığı kaldırma kuvvetidir. Bir akışkan içerisinde ya da üzerindeki bir cisme, cismin batan kısmının hacmi ve akışkanın öz ağırlığı ile orantılı bir kaldırma kuvveti etki eder.

R = V _batan . p . g

Bu eşitlikte R kaldırma kuvveti, V _batan kısmı hacmi, p akışkanın yoğunluğu ve g yerçekimi ivmesidir. Bu ifade ilk kez Archimedes tarafından ortaya konmuştur. Ünlü matematik ve Fizik bilgini Archimedes’in hacim ve alan hesaplarıyla ilgili birçok buluşu vardır. Kaldıraç ve kaldırma kuvveti ile ilgili ilk çalışmaları yapan da Archimedes’tir.

Kitabınızın 100. Sayfasında yer alan Şekil 4.5’te görüldüğü üzere

R > W ise, cisim sıvı içinde yüzeye doğru hareket eder ve bir kısmı sıvı üzerinde kalacak şekilde yüzer,

R = W ise, cisim sıvı içerisinde dengede kalır,

R < W ise, cisim sıvı tabanına batar.

Yüzey Gerilimi ve Vizkozite

Yoğunluğu p olan bir akışkan, bir tüpe oval bir yüzey oluşur. Bu yüzeyin ovalliği aşağı doğru (konkav) olabileceği gibi yukarı doğru (konveks) da olabilir. Bunun sebebi yüzey gerilim etkisidir. Islanma, sıvıların katı yüzeylerle ara yüzler oluşturma yeteneğidir. Sıvı ile katı yüzey arasındaki temas açısı 0, ıslanma derecesinin bir ölçüsüdür.

Bir sıvının katı bir yüzeyi ıslatıp ıslatmayacağı, sıvı molekülleri arasındaki kohezyon kuvvetleri ile sıvı molekülleri ile kabı oluşturan moleküller arasındaki kohezyon kuvvetlerinin bağıl büyüklüğü ile belirlenir. Örneğin su damlası camı ıslatır çünkü su molekülleri cam moleküllerine, diğer su moleküllerine oranla daha güçlü bir şekilde çekilir. Ancak su yerine cıva düşünüldüğünde bunun tam tersi gerçekleşir ve civanın camı ıslatmadığı görülür.

Sıvı moleküllerinin arasındaki kohezyon kuvvetinin, akışkan ile kabın yüzeyi arasında oluşan adhezyon kuvvetinden büyük olması durumunda sıvı yüzeyinde içbükey bir eğrilik, tersi durumda ise dışbükey bir eğrilik oluşur.

Bir akışkanın akmaya karşı gösterdiği dirence viskozite adı verilir. Örneğin sıvı haldeki bir akışkan düz bir yüzey üzerinde akıyorsa, yüzeyle temas halindeki sıvı tabakası adezyon kuvveti nedeniyle hareketsiz kalır, onun üstündeki sıvı molekülleri ilk tabaka üzerinde yavaş hareket eder, üçüncü tabaka ise ikinciye göre daha hızlı hareket eder. Yüzeyden uzaklaştıkça sıvı tabakalarının hızı büyür. Bir sıvının, sıcaklık arttıkça viskozitesi azalır. Akışkanların viskozitelerini gösteren h katsayısının birimi Ns/m ² dir. Kitabınızın 102. sayfasında yer alan Tablo 4.1’de çeşitli sıvıların viskozite katsayıları verilmiştir.

Çevremizde akışkanların fiziksel özelliklerini yansıtan olayları sıklıkla görürüz. Ağaçların ve bitkilerin yapraklarına suyun ulaşmasını sağlayan kılcallık olayıdır. Bitkilerin köklerinden yapraklarına kadar uzanan odunsu dokular aslında minicik odun borulardır. Bu borularda hem adezyon hem de kohezyonu sonucu su molekülleri yer çekiminin etkisine rağmen yükselir ve bitkinin her yaprağına ulaşır. Süngerin ve peçetenin sadece bir ucu suya değse dahi tamamı ıslanır. Süngerin ve peçetenin yapıldığı malzemenin içinde küçük boşluklar vardır. Bu boşluklarla su molekülleri arasındaki adezyon kuvveti, suyun boşlukların içine doğru ilerlemesini sağlar. Bir sıvıya bir küp şekerin sadece alt kısmı değdirilirse, sıvının küp şekerde yükseldiğini görülür. Sıvı, şekerin arasındaki boşluklardan kılcallık olayı nedeniyle yükselir.

Hız ve Basınç İlişkisi, Bernoulli Prensibi

Akışkanların hareketini inceleyen fiziğin bir alt dalına akışkan dinamiği, akışkanlarda akış hızı ve akışkan basıncı ilişkisini açıklayan süreklilik denklemi de Bernoulli denklemi adını alır. Bir akışkan eğer boru gibi sınırlayıcı bir kabın içinde akıyorsa, bu tür akış türüne iç akış , eğer böyle fiziksel bir sınır yoksa dış akış olarak tanımlanır. Otomobil, uçak ve gemilerin etrafındaki hava akışı dış akıştır. İç akışlar laminer akış ya da türbülanslı akış olarak incelenebilir.

Laminer akış durumunda akışkanın akış hızı zaman içinde değişmez, sabit kalır. Akışkanın içinde bulunduğu kanalın sınır yüzeyleri bir başka cisme temas etmesi ya da akışkanın kendi içindeki sürtünmesi akış hızında düzensiz değişikliklere neden olabilir. Bu tür düzensiz akışa türbülanslı akış ya da girdap akışı denir. Türbülanslı akış çok düzensiz ve karmaşık olabilir.

Akışkan akışını incelemek için kullanılan araçlardan biri akış çizgisi ya da akış yoludur. Akışkanın içinde olduğu varsayılan bir parçacığın akış ile birlikte izlediği yola akış yolu ya da akış çizgisi denir. Akışkanın hız vektörü ve akış çizgileri daima birbirine paraleldir.

Yüz ve Hız İlişkisi, Süreklilik Denklemi

Yüzey alanları A ₁ ve A ₂ olan iki borudan akan akışkanın bir bölgede v ₁ ve diğer bölgede v ₂ hızıyla ilerlediği kabul edilsin. A ₁ ve A ₂ yüzey kesit alanlarından bir saniyede A ₁ .v ₁ =A ₂ .v ₂ kadar akışkan eşit olarak yer değiştirir. Bu eşitlik; Süreklilik Denklemi olarak bilinir.

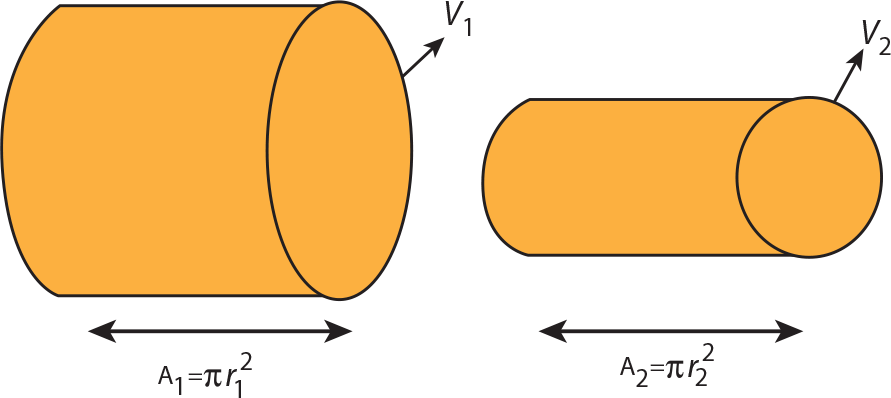
Bu iki akışkanın kütlesi birbirine eşit olduğundan,

Bunun sonucunda da

v ₁ / v ₂ = r ₂ ² / r ₁ ²

hızların oranının yarıçapların oranları ile ters orantılı olduğu sonucuna ulaşırız.

Hareket Halindeki Bir Akışkanın Enerjisi: Bernoulli Denklemi

Bir akışkan içerisinde 1 ve 2 gibi iki nokta seçilsin. Akışkan 1 noktasından geçerken, bu akışkan kütlesi arkasındaki akışkan kütle tarafından itilir. Dolayısıyla kendisine karşı bir iş yapılmış olur. Akışkan 2 noktasından geçerken de kendi önünde olan akışkanı iter, dolayısıyla iş yapar. Eğer kendi yaptığı iş, kendisine yapılan işten fazla ise, yaptığı net iş sürtünmeye harcanmadığı takdirde bir noktadan diğerine akarken potansiyel ve kinetik enerjisinin ne kadar değişmiş olduğunu gösterir.

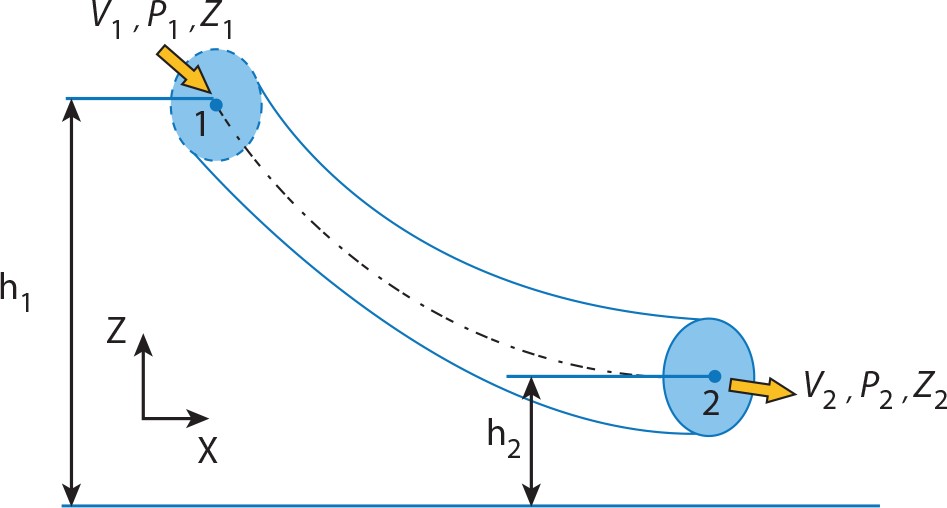
Şekilde sıkışamaz ve sürtünmez farz edilen ve kesiti değişken bir boru içerisinde kararlı bir tarzda akan, laminer akışa uygun yavaş kabul edilen düzgün akan bir akışkan olduğu varsayılsın. 1 noktasının yer aldığı yüzey alanı A ₁ ve 2 noktasının yer aldığı yüzey alanı A ₂ olsun. Bu yüzeylerden akışkanın geçiş hızı ise sırasıyla v ₁ ve v ₂ , akışkan basıncı ise P ₁ ve P ₂ ’dir. Süreklilik denkleminden

A ₁ . v ₁ = A ₂ . v ₂

olacaktır. Akışkan sıkıştırılamaz kabul edilirse, bir t süresince her kesitten aynı kütleli akışkan geçecektir. Akışkanın yoğunluğu p ise, bu kütlenin hacmi; ile verilir. Bu akışkan 1 no’lu h ₁ yüksekliğindeki noktada;

mgh1 potansiyel enerjisine, v ₁ hızından dolayı 2 kinetik enerjisine, P ₁ basınçlı bir bölgeye girişe zorlamak için de eşitliğinden P ₁ V işine ihtiyaç vardır.

Akışkanı 1 no’lu noktadan 2 no’lu noktaya getirmek için yapılması gereken iş, sürtünme olmadığı varsayıldığından toplam enerjideki değişime eşittir:

Eşitliğin her bir terimi r/m ile çarpılırsa;

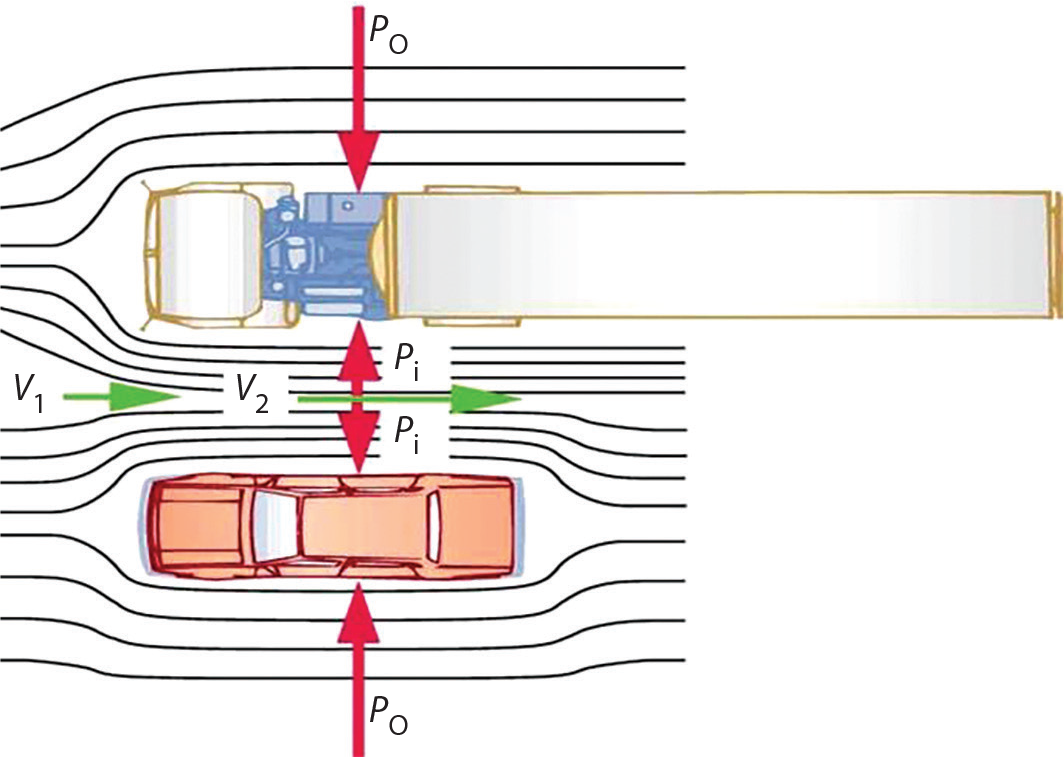
bulunur. Yukarıdaki eşitlik, İsviçreli bilim adamı Daniel Bernoulli’e atfen Bernoulli Denklemi olarak anılır. Bu eşitlikten bir sıvının bir noktadan aynı seviyedeki bir başka noktaya giderken hızı arttığı takdirde basıncının azalacağı görülebilir. Örneğin iki gemi durgun suda yan yana aynı yönde ve aynı hızla gidiyorsa, sanki gemiler duruyor da su ters yönde bağıl olarak gemilerin hızıyla akıyormuş gibi görünür. Su gemiler arasındaki dar bölgeye girerken hızı artar ve basıncı azalır. Gemilerin dış taraflarındaki basınç daha büyük kalacağından, her iki gemiyi de içe doğru iten bir etki yaratır. Aynı durum aşağıda şekilde verilen bir tır ile otomobilin yan yana geçiş olaylarında da görülür.