Sağlık Alanında İstatistik Dersi 3. Ünite Özet

Olasılık Kavramı

Genel anlamıyla herhangi bir olayın gerçekleşme şansının sayısal ölçümüne olasılık adı verilir. Buna göre olasılık, olaylara ilişkin belirsizlik derecesinin ölçüleri olarak kullanılabilir. Eğer olasılık mevcutsa olayların gerçekleşme şansı tespit edilebilir.

Olasılık değerleri, daima 0 ile 1 arasında bir değer alır. Olasılık değerinin 0 olması olayın gerçekleşme şansının bulunmadığını, 1 olması ise olayın kesinlikle gerçekleşeceğini göstermektedir. 0 ile 1 arasındaki olasılık değerleri, olayın gerçekleşme şansının derecesini temsil eder.

Olası gözlemlerden yalnızca birinin gerçekleşmesi ile sonuçlanan sürece deney adı verilir. Deneyin sona erme biçimine ise sonuç adı verilir. Bir deneyin iki ya da ikiden fazla olası sonucu bulunur ve bu sonuçlardan hangisinin gerçekleşeceği belirsizdir. Dolayısıyla deney, iyi tanımlanmış sonuçlar üreten bir süreç olarak da tanımlanabilir. Bir deneyin herhangi bir tekrarında, olası sonuçlardan yalnızca bir tanesi gerçekleşir.

Bir deneyde olası tüm sonuçların belirlenmesiyle, bu deney için örneklem uzayı tanımlanmış olur. Dolayısıyla bir deneyin tüm olası sonuçlarından oluşan kümeye örneklem uzayı adı verilir ve bu küme S harfi ile gösterilir. Deneyin olası tüm sonuçlarına örneklem uzayının bir elemanı karşılık gelir. Bu elemana örneklem uzayı noktası adı verilir. Bir deneyin bir ya da daha fazla sonucundan oluşan kümeye ise bir olay adı verilir. Dolayısıyla olay, örneklem uzayının herhangi bir alt kümesi olacaktır.

Sayma Kuralları ve Olasılık Hesaplama Yöntemleri

Olası sonuçların belirlenmesi ve sayılması, olasılıkların hesaplanabilmesi için gerekli bir adımdır.

ncelenecek ilk sayma kuralı çok-adımlı deneyler için geçerlidir. Örnek olarak iki adet bozuk para atma deneyinde olası sonuçlar, bu iki paranın üst yüze gelen yazı ya da tura şekillerine göre tanımlanmış olsun. Şimdi bu deney için olası sonuç sayısının kaç olduğunu belirlensin. İki adet bozuk para atma deneyi iki-adımlı bir deney olarak düşünülebilir. Bu deneyin birinci adımı ilk paranın atılması, ikinci adımı ise ikinci paranın atılmasıdır. Paranın yazı gelmesi “Y” ile, tura gelmesi de “T” ile belirtilirse (Y, T) ifadesi, “Birinci paranın yazı gelmesi ve ikinci paranın tura gelmesi” olayını gösterecektir. Buna göre, bu deney için örneklem uzayı:

S = {(Y, Y), (Y, T), (T, Y), (T, T)}

biçiminde olacaktır. Dolayısıyla bu deney için olası sonuç sayısı dörttür. Bu durumda, tüm olası sonuçlar kolaylıkla listelenebilir. Çok-adımlı deneyler için geliştirilen saymanın temel ilkesi yardımıyla herhangi bir listeleme yapmaya gerek kalmadan deneylerin olası sonuç sayısı belirlenebilir. Bu ilkeye göre; eğer bir deney, birinci adımında n ₁ olası sonuç, ikinci adımında n ₂ olası sonuç,

k-inci adımında nk olası sonuç bulunan k adımlı bir deney olarak tanımlanabiliyorsa bu deney için toplam olası sonuç sayısı (n ₁ ) (n ₂ )... (n _k ) olarak verilir.

İkinci sayma kuralı olan kombinasyon yardımıyla, N sayıda nesne arasından n adet nesnenin diziliş sırası dikkate alınmadan kaç farklı biçimde seçilebileceği yani bu seçimdeki olası sonuç sayısı belirlenebilmektedir. Buna göre, N sayıda nesneden n tanesi (n?N) rastgele olarak seçilir ve n birim herhangi bir sırada yazılırsa buna n-dereceli kombinasyon adı verilir. Buna göre;

“N sayıda nesne arasından tek bir seferde yapılabilecek n birimlik kombinasyon sayısı, 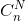, 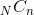ya da ile gösterilir.

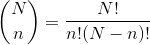
eşitliği yardımıyla hesaplanır. Özel olarak, 0! = 1 ve 1! = 1 olur. Eşitliklerdeki “!” simgesi faktöriyel olarak okunur.

Üçüncü sayma kuralı olan permütasyon yardımıyla N sayıda nesne arasından n adet nesnenin seçim sırası önemli olduğunda kaç farklı biçimde seçilebileceği belirlenebilmektedir. Görüldüğü gibi, permütasyon ile kombinasyon arasındaki fark; seçim esnasında nesnelerin diziliş sıralaması kombinasyonda önemli değil iken permütasyonda bu sıralamanın önemli olmasıdır. Örneğin, X, Y ve Z ile belirtilen üç adet nesneden iki tanesi, bu nesnelerin seçim sırası önemli olacak şekilde seçilmek istensin. Bu durumda (XY), (YX), (XZ), (ZX), (YZ) ve (ZY) olmak üzere 6 farklı seçim yapılabilir. Aynı üç nesnenin ikili kombinasyonu belirlenmek istenseydi, kombinasyonda nesnelerin sıralaması önemli olmadığı için örneğin (XY) ile (YX) aynı seçimler olacaktı. Bu durumda ise ancak 3 farklı seçim yapılabilecekti. Tanım olarak vermek gerekirse, n sayıda elemandan oluşan bir kümenin herhangi bir alt kümesinden yapılan her farklı sıralamaya bir permütasyon denir. Permütasyon; N sayıda nesne arasından tek bir seferde yapılabilecek n birimlik permütasyon sayısı, 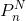, 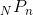ile gösterilir.

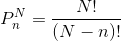
eşitliği yardımıyla hesaplanır.

Olasılık hesaplama için en sık kullanılan üç yaklaşım; klasik yöntem, göreli frekans yöntemi ve öznel (subjektif) yöntemdir. Ancak kullanılan yöntem hangisi olursa olsun, olasılık hesaplamalarında aşağıda belirtilen iki temel kuralın sağlanması zorunludur.

1. Olası her bir deney sonucunun gerçekleşme olasılığı 0 ile 1 (0 ve 1 değerleri dahil değerleri arasında yer almalıdır.
2. Olası tüm deney sonuçlarının gerçekleşme olasılıklarının toplamı 1’e eşit olmalıdır.

Olaylar ve Olayların Olasılıkları

Örneklem uzayının herhangi bir alt kümesini oluşturan elemanlarla herhangi bir olay belirlenebilir. Bu alt küme, örneklem uzayında bulunan ve olayın gerçekleştiği tüm elemanları içerir. Buna göre, örneklem uzayı noktalarının bir topluluğuna olay adı verilir. Dolayısıyla tanımlanan herhangi bir olay, örneklem uzayının bir alt kümesi olacaktır. Bir olayın gerçekleşme olasılığı ise bu olaydaki olası sonuçların olasılıkları toplamına eşittir.

Verilen bir A olayının tümleyeni, örneklem uzayında A olayının dışında kalan tüm örneklem uzayı noktalarını içeren olay olarak tanımlanır ve AT olayının tümleyeni ile gösterilir.

Toplama kuralı, örneklem uzayında yer alan A ve B gibi herhangi iki olaydan en az birinin gerçekleşme olasılığının hesaplanmasında kullanılır. Bir diğer deyişle A olayının veya B olayının ya da her ikisinin birden gerçekleşme olasılığı araştırılırken toplama kuralından yararlanılır. Toplama Kuralı;

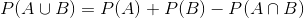
Örneklem uzayında yer alan herhangi iki olayın ortak örneklem uzayı noktası bulunmuyor ise bu olaylara ayrık olaylar adı verilir. Tanıma göre, S’de yer alan A ve B gibi herhangi iki olay ayrık olay ise, bu olayları ifade eden kümelerin ortak elemanı bulunmamaktadır. Bir diğer deyişle, A ve B ayrık olaylar ise bu olayların kesişimi yoktur(A?B=Ø) . İki olay ayrık olduğunda, bu olaylardan biri gerçekleşirken diğeri gerçekleşemez. Bu durumda ise P(A?B)= 0 olur.

Koşullu Olasılık

Bazı durumlarda bir olayın gerçekleşme olasılığı, bu olayla ilişkili başka bir olayın daha önce gerçekleşip gerçekleşmediğinden etkilenir. Söz gelimi, A olayının gerçekleşme olasılığı P(A) olsun. A olayı ile ilişkili bir B olayının da önceden gerçekleştiği bilgisi elde edilmiş olsun. Böylece, A olayı için yeni bir olasılık hesaplanarak, elde edilen bu yeni bilgiden de yararlanılmak istenebilir. Buna göre, B olayının gerçekleştiği bilindiğinde, A olayının gerçekleşme olasılığı koşullu olasılık olarak adlandırılır ve bu olasılık P(A|B) ile gösterilir. “|” gösterimi, herhangi bir olayının gerçekleşme koşulu altında bir diğer olayın koşullu olasılığını belirtmede kullanılır. Buna göre, P(A|B) gösterimi, “B bilindiğine göre, A’nın koşullu olasılığı” biçiminde okunur.

Örneklem uzayında yer alan A ve B gibi herhangi iki olay için bu olaylardan herhangi birinin gerçekleştiğinin bilinmesi, diğerinin gerçekleşme olasılığını değiştirmiyor ise bu iki olaya bağımsız olaylar adı verilir. Bunun tersi duruma, yani bu iki olaydan herhangi birinin gerçekleştiğinin bilinmesi diğerinin gerçekleşme olasılığını etkiliyorsa böyle olaylara da bağımlı olaylar denir.

Olasılıkta toplama kuralı, örneklem uzayında yer alan herhangi iki olayın birleşiminin (birinin veya ötekinin) gerçekleşme olasılığının hesaplanmasında kullanılırken, çarpma kuralı iki olayın kesişiminin (iki olayın aynı anda) gerçekleşme olasılığını hesaplamada kullanılır ve koşullu olasılık tanımına dayalı olarak verilir. Koşullu olasılık tanımında verilen eşitlikler P(A?B) için çözülürse, olasılıkta çarpma kuralı; P(A?B) = P(A)P(B|A)ya da P(A?B) = P(B)P(A|B) olarak elde edilir.

Koşullu olasılıkta yeni bir bilgi elde edildiği zaman olasılıkların değişmesi, olasılık çözümlemesinin önemli bir evresini oluşturmaktadır. Çoğu durumda çözümlemeye, incelenen belirli bir olay için başlangıç ya da önsel olasılıklar tahmin edilerek başlanır. Eldeki mevcut bilgi seviyesine dayalı başlangıç olasılığına önsel olasılık adı verilir. Ardından, örneklem verileri ya da özel bir rapor vb. gibi kaynaklardan olaylara ilişkin ek bilgiler elde edilebilir. Bu yeni bilgiler göz önüne alındığında, önsel olasılık değerleri yeni olasılıklar hesaplanarak güncellenir ve güncellenen bu olasılıklar sonsal olasılıklar olarak adlandırılır. Bayes teoremi ise bu sonsal olasılıkların hesaplanmasında kullanılan bir araçtır. Bayes teoremi kullanıldığında, olasılık değişim sürecinde izlenecek adımlar sırasıyla önsel olasılıkların hesaplanması, yeni bilgilerin elde edilmesi, Bayes teoreminin uygulanması, sonsal olasılıkların hesaplanmasıdır.

Bayes teoremi izleyen tanımla verilebilir. A1, A2, ..., An olayları, n adet karşılıklı ayrık ve bütüne tamamlayan (birleşimleri örneklem uzayına eşit olan) olaylar olsun. Bayes teoremine göre, B olayının gerçekleştiği bilindiğine göre, Ai’nin gerçekleşme olasılığı;

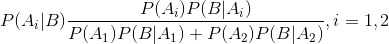
eşitliği ile hesaplanır.

Rassal Değişkenler ve Olasılık Dağılımları

Sayısal değerler yardımıyla bir deneydeki olası sonuçların tanımlanmasında bir araç olarak rassal değişkenler kullanılır. Dolayısıyla rassal değişkenlerin sayısal değerler olduğu kabul edilir. Buna göre, bir deneyin herhangi bir olası sonucunun sayısal değerine rassal değişken adı verilir. Rassal değişkenler, deneyden deneye farklı değerler alabilen ve aldığı bu değerleri belli bir olasılıkla alan değişkenlerdir.

Sonlu sayıda değer alabilen ya da 0, 1, 2,..., gibi sonsuz bir sayı dizisi olarak kabul edilen rassal değişkene kesikli rassal değişken adı verilir. Örneğin “Bir hastanenin acil servisine son bir ay içinde başvuran hasta sayısı” rassal değişkenini düşünelim. Bu rassal değişkenin alabileceği değerler 0, 1, 2,..., gibi bir tamsayılar dizisidir. Buna göre belirtilen rassal değişken, bu sonsuz sayı dizisinde yer alan değerlerden birini alacağı için kesikli bir rassal değişkendir.

Bir sayı aralığı ya da aralıklar kümesi üzerinde herhangi bir sayısal değer alabilen rassal değişkene sürekli rassal değişken adı verilir. Zaman, ağırlık, uzaklık ya da hava sıcaklığı gibi ölçülere dayalı deneysel sonuçlar belli bir aralıkta sonsuz sayıda değer alabileceği için sürekli rassal değişkenlerdir.

Bir rassal değişkenin olasılık dağılımı, olasılıkların bu rassal değişkenin olası değerleri üzerinde nasıl dağıldığını tanımlayan bir fonksiyondur. X kesikli rassal değişkeni için olasılık dağılımına olasılık fonksiyonu adı verilir ve bu fonksiyon P(x) ile gösterilir. Olasılık fonksiyonu, rassal değişkenin her bir değeri için olasılıkların bulunmasında kullanılır.

Ortalama, olasılık dağılımlarının merkezi eğilimini gösteren tipik bir değerdir ve bir olasılık dağılımının ortalamasına, o olasılık dağılımının beklenen değeri adı verilir. Beklenen değer, bir rassal değişkenin aldığı değerlerin, bu rassal değişkenlere ilişkin olasılıklarla ağırlıklandırıldığı bir ağırlıklı ortalamadır. Kesikli bir rassal değişkeninin beklenen değeri aşağıdaki eşitlik yardımıyla hesaplanır:

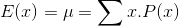
Beklenen değer, rassal değişken için ortalama değeri vermekle birlikte, dağılımın değişkenliğini ya da yayılımını ölçen bir ölçü değildir. Bilindiği gibi, eldeki veriler için hesaplanan en önemli değişkenlik ölçülerinden biri varyanstır. Bir rassal değişkenin aldığı değerlerdeki değişkenliğin belirlenmesinde de varyanstan yararlanılabilir.

Binom dağılımı, uygulamalarda çok sık rastlanan kesikli olasılık dağılımıdır. Dağılımın en önemli özelliği, aynı koşullarda tekrarlanan deneylerin her tekrarında yalnızca iki olası sonuç bulunur. Örneğin, tek bir zar atma deneyinde, zar ya tek sayı ya da çift sayı gelecektir. Atılan bu zarın sonucu aynı anda hem tek sayı hem de çift sayı olamayacağına göre, bu iki olası sonuç ayrıktır

Kesikli ve sürekli rassal değişkenler arasındaki temel farklılık, olasılıkların hesaplanma yöntemi bakımından ortaya çıkmaktadır. Kesikli rassal değişkenler için P(x) olasılık fonksiyonu, rassal değişkenin belirli bir değeri alma olasılığının hesaplanmasında kullanılır. Sürekli rassal değişkenlerde ise olasılık fonksiyonunun karşılığı olarak olasılık yoğunluk fonksiyonu ifadesi kullanılır ve bu fonksiyon f (x) ile belirtilir. Olasılık fonksiyonu ile olasılık yoğunluk fonksiyonu arasındaki fark, P(x) yardımıyla rassal değişkenin tek bir değerine ilişkin olasılık hesaplanabilirken, f (x) olasılık yoğunluk fonksiyonu kullanılarak tek bir değer için direkt olarak olasılık hesaplanamamaktadır. Bununla birlikte, rassal değişkenin tanım bölgesinde yer alan belirli bir aralıkta f (x) fonksiyonunun altında kalan alan, X sürekli rassal değişkeninin belirlenen aralıkta bir değer alma olasılığını vermektedir. Bu nedenle, sürekli rassal değişkenler için olasılık hesaplanırken, rassal değişkenin belli bir aralıkta yer alma olasılığı hesaplanmış olur.

Normal olasılık dağılımı, sürekli rassal değişkenlerin tanımlanması bakımından en önemli olasılık dağılımıdır. Normal dağılımın günlük yaşantıda pek çok farklı alanda uygulaması bulunmaktadır. Örneğin, insanların uzunluğu, ağırlığı, gıdaların raf ömürleri, bilimsel ölçüm değerleri, belli bir bölgeye düşen yağış miktarı vb. gibi sürekli rassal değişkenlerin birçoğunun olasılık dağılımı normal dağılımdır.

Eğer bir rassal değişken, aritmetik ortalaması 0 ve standart sapması 1 olan normal dağılıma sahipse, bu rassal değişkenin standart normal dağılıma sahip olduğu söylenir.