Lojistik Maliyetleri ve Raporlama 2 Dersi 6. Ünite Özet

Giriş

Diğer tüm faaliyetlerde olduğu gibi lojistik faaliyetlerde de geleceğe ilişkin planlama yapmak ve farklı stratejik kararlar almak için maliyet, hacim ve kâr analizlerine ihtiyaç duyulur. Maliyet, hacim ve kâr analizlerinde öncelikle toplam maliyet fonksiyonunun oluşturulması gerekmektedir. Toplam maliyet fonksiyonunun oluşturulabilmesi için maliyetlerin faaliyet hacmi ile ilişkilerinin ortaya konması ve maliyetlerin davranış şekillerinin bilinmesi gerekir. Faaliyet hacmi ile olan ilişkilerine göre maliyetler sabit, değişken, yarı sabit ve yarı değişken şeklinde bir sınıflandırmaya tabi tutulmaktadır.

Toplam Lojistik Maliyet Fonksiyonu

İşletmeler lojistik maliyetlerini hedef maliyetleme, misyon maliyetleme, faaliyete dayalı maliyetleme, toplam maliyet analizi (modeli) yaklaşımı gibi muhasebe içi yöntemlerle veya geçmiş deneyimlere bağlı olarak tahmini bir rakam, satışların veya maliyetlerin bir yüzdesi cinsinden muhasebe dışı yöntemlerle de belirleyebilmektedirler. Günümüzde lojistik maliyetlerin hesaplanması ve analizinde “toplam maliyet analizi yaklaşımı” işletmelere büyük kolaylık sağlamaktadır. Bu yaklaşıma göre, lojistik faaliyetler sonucu ortaya çıkan ürünün değeri, ağırlığı ve hacminin lojistik maliyetlere olan etkisi matematiksel denklem ile analiz edilmektedir. Buna göre işletmeler lojistik maliyetlerini sabit ve değişken olarak ayrı ayrı belirlemeleri ve toplam maliyet fonksiyonunu oluşturmaları gerekmektedir. Toplam maliyet fonksiyonu doğrusal veya eğrisel fonksiyon şeklinde ifade edilebilir. Lojistik maliyetler arasındaki ilişkinin doğrusal olduğu varsayımı altında toplam lojistik maliyetlere ilişkin matematiksel denklem y = ax + b şeklinde olacaktır. Bu fonksiyonda “y” bağımlı değişken olan toplam lojistik maliyeti, “x” bağımsız değişken olan faaliyet hacmini (üretim miktarını), “a” bağımsız değişkendeki bir birimlik değişmenin bağımlı değişkende neden olduğu değişmeyi (birim değişken lojistik maliyeti) ve “b” ise toplam sabit lojistik maliyeti temsil etmektedir.

Sabit Ve Değişken Maliyetlerin Belirlenmesinde Kullanılan Yöntemler

İşletmelerde toplam lojistik maliyet fonksiyonunun oluşturulabilmesi için gerekli olan sabit ve değişken lojistik maliyetlerin belirlenmesinde değişik yöntemlerden yararlanılmaktadır. Bu yöntem ve teknikler üç başlık altında toplanabilir:

• Analitik Yöntem
• Muhasebe Yöntemi
• Matematik ve İstatistik Teknikler

Analitik yöntemde; lojistik maliyet unsurları (taşıma maliyetleri, depolama maliyetleri, sipariş ve bilgi süreci maliyetleri, her parti mala ilişkin maliyetler ve stok bulundurma maliyetleri) ile faaliyet hacmi arasındaki ilişkisini ortaya koymak için fiziki tüketim miktarları esas alınır. Bu yöntemde lojistik maliyetlerle faaliyet hacmi arasındaki ilişkiler genellikle mühendisler tarafından belirlenmesi nedeniyle, bu yöntem “mühendislik yöntemi” olarak da bilinmektedir. Analitik yöntemde, maliyetlerle iş (faaliyet) hacmi arasındaki fiziksel (miktar) ve parasal (TL) bağlantıların ayrı ayrı incelenmesinin maliyetli bir iş olması nedeniyle toplam maliyetlerin analizinde analitik yöntemin kullanımı oldukça sınırlıdır. Ancak maliyetleri oluşturan unsurların hem miktar hem de tutar olarak değişimlerinin kolaylıkla izlenmesine olanak vermektedir. Fiyat değişimlerinin toplam maliyeti nasıl değiştirdiği kolaylıkla gözlenebilmektedir. Bu yöntemde fiili çalışmalar sonucu ortaya çıkan verimsizlik ve savurganlıkların ortaya çıkmasını ve maliyet kontrolünün yapılabilmesini sağlar. Analitik yöntem, geçmişe ait kayıt ve gözlemlerin bulunmadığı ya da yetersiz olduğu durumlarda, maliyetlerin davranış biçimlerinin belirlenmesinde kullanılabilmektedir. Aynı zamanda bu yöntem ile kapasitede yapılması düşünülen değişikliklerden sonra maliyetlerin nasıl davranış göstereceklerinin tahmininde kullanılabilmektedir.

Muhasebe yönteminde toplam maliyet fonksiyonu, işletmenin muhasebe kayıtlarından hareket edilerek oluşturulmaya çalışılır. Bu yöntem iki aşamada uygulanmakta olup 1. aşamada İşletme kendisinin belirlemiş olduğu bir dönem aralığına ilişkin faaliyet hacimlerindeki değişim yüzdeleri ile maliyet kalemlerindeki değişim yüzdelerini karşılaştırır. 2. aşama ise Maliyet kalemleri sabit veya değişken maliyetler olmak üzere ikiye ayrılır. Yarı değişken maliyetler, sabit ve değişken kısımlarından hangisi daha ağır basıyorsa, o maliyet türü içerisine dâhil edilir. Yukarıda belirtilen karşılaştırma sonucunda maliyet kalemlerindeki yüzdesel değişimin yönü ve rakamı, faaliyet hacmindeki değişme yüzdeleri ile aynı yönde ve rakamlar birbirine yakın ise bu maliyetler değişken maliyet olarak kabul edilir. Ancak maliyet kalemlerindeki değişimin yönü aynı veya ters olup, rakamlar sıfıra yakın ise bu maliyetler sabit maliyet olarak kabul edilir.

Matematik ve istatistiksel teknikler, lojistik maliyetler ile faaliyet hacmi arasında geçmiş dönemlerdeki ilişkilerin ortaya çıkarılmasında kullanılır. Matematik ve istatistiksel teknikler kullanılarak elde edilen sonuçların sağlıklı olabilmesi için, mümkün olduğu kadar çok sayıda dönemin hesaplamalara dâhil edilmesi gerekmektedir. Ancak hesaplamaya dâhil edilen dönemlerin işletmenin normal faaliyetlerini gerçekleştirdiği dönemler olması, arızi (olağanüstü) dönemlerdeki verilerin hesaplamaya dâhil edilmemesi gerekir. Lojistik maliyetler ile faaliyet hacmi arasındaki ilişkilerin belirlenmesinde kullanılan matematik ve istatistiksel teknikler:

• En yüksek ve en düşük hacimler yöntemi,
• Çifte ortalamalar yöntemi,
• Grafik yöntemi,
• En küçük kareler yöntemlerinden oluşur.

En yüksek ve en düşük hacimler yöntemine göre; lojistik maliyetler ile faaliyet hacmi arasındaki ilişki belirlenirken, olağanüstü dönemlerdeki verilerin hesaplamaya dâhil edilmemesine özen gösterilerek, seçilen dönemlerden faaliyet hacmi en yüksek olan ile faaliyet hacmi en düşük olan dönem esas alınır. Seçilen bu iki döneme ilişkin lojistik maliyetler arasındaki fark, faaliyet hacimleri arasındaki farka bölünür.

Birim değişken maliyetin (a) hesaplanması aşağıdaki gibi formüle edilebilir:

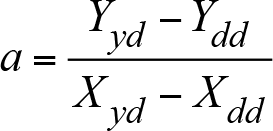
a= Birim değişken maliyet
Y= Toplam maliyet
X= Faaliyet hacmi
yd= Yüksek dönem
dd= Düşük dönem

Çifte Ortalamalar Yöntemi, en yüksek ve en düşük hacimler yönteminin ileri bir aşamasıdır. Birim değişken ve toplam sabit maliyetin bulunması için yapılan hesaplamalar, sadece dönemlerin seçilmesinde farklılık gösterir. Çifte ortalamalar yönteminde analiz yapılacak dönemler, “yüksek faaliyet hacmi dönemleri” ve “düşük faaliyet hacmi dönemleri” şeklinde eşit iki gruba ayrılır ve bu dönemlerin ortalama değerleri üzerinden hesaplamalar yapılır. Bu nedenle “Çifte Ortalamalar Yöntemi”, “Yarı Ortalama” ve “Yüksek ve Düşük Ortalamalar” yöntemi şeklinde de adlandırılabilir.

Lojistik işletmelerinde toplam maliyet fonksiyonunun belirlenmesinde kullanılan bir diğer matematiksel yöntem ise grafik yöntemdir. Bu yöntemde faaliyet hacim ilişkilerinin belirlenmesinde dağılım grafiklerinden yararlanılmaktadır. Dağılım grafiği çizilirken yatay eksende (x) faaliyet hacmine, dikey eksende (y) ise faaliyet hacmi ile ilişkisi kurulacak olan toplam karma lojistik maliyetlere yer verilir. Her döneme ilişkin faaliyet hacmi ile o faaliyet hacmindeki karma lojistik maliyetler bir düzlem üzerinde nokta şeklinde işaretlenir. Bütün eşleştirmeler bittikten sonra bu noktaları en iyi ifade eden bir toplam maliyet doğrusu çizildikten sonra bu doğru üzerinde rastgele iki nokta belirlenir. Toplam maliyet doğrusunun eğimi, (a) parametresini bir başka ifadeyle birim değişken lojistik maliyeti verir. Grafik yöntem, faaliyet hacmi ile toplam maliyet arasındaki bütünsel ilişkiyi görme açısından işletmelere önemli fayda sağlayan bir yöntemdir.

En küçük kareler yönteminde ise, dağılım grafiğinde yer alan noktaları temsil edecek en uygun lojistik maliyet regresyon doğrusunun çizilmesidir. Bu yöntemde regresyon doğrusu göz kararı değil, istatistiksel analizler yardımıyla çizilir. Bu yöntemin amacı, dağılım grafiğindeki çeşitli noktalardan olan düşey uzaklıkların karelerinin toplamının en küçük olduğu doğrunun denkleminin nesnel (objektif ) olarak saptanmasıdır.

En küçük kareler yönteminde, toplam maliyet doğrusu denklemini oluşturabilmek için gerekli olan (a) ve (b) parametrelerini hesaplamak için, normal denklemler adı verilen aşağıdaki denklem sisteminden yararlanılır.

SXY = aS x2+ bSx

SY = aSx + bn

Denklemlerdeki simgelerin anlamları aşağıda verilmiştir:

Y = Gözlenen toplam karma maliyet
X = Faaliyet ölçüsü
a = Birim değişken maliyet
b = Toplam sabit maliyet
n = Gözlem sayısı

Bu denklemlerden a ve b parametreleri aşağıdaki gibi formüle edilebilir:

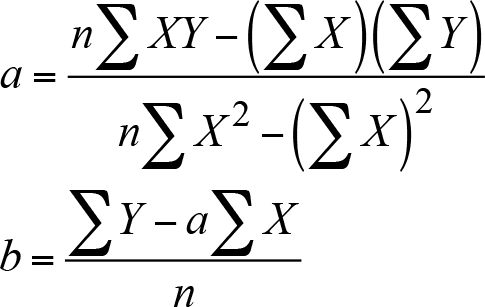
Lojistik Faaliyetlerde Maliyet - Hacim - Kâr Analizi

Maliyet-Hacim-Kâr analizi, işletmenin belli bir dönemde ve belli bir faaliyet aralığında gelir, maliyet ve kâr ilişkilerini sistematik şekilde analiz etme sürecidir. Lojistik işletmelerinde maliyet-hacim-kâr analizi yapılırken toplam maliyet fonksiyonu ve kâr fonksiyonundan yararlanılır. İşletmenin kârı, belli bir dönemde gerçekleşen toplam gelir ile toplam gider arasındaki olumlu farktır. Belli bir dönemde gerçekleşen gelir ile gider arasındaki olumsuz fark ise zarar olarak ifade edilir. Bu anlamda kâra ilişkin eşitlik aşağıdaki gibi yazılır.

Kâr = Toplam Gelir – Toplam Gider

Satış miktarının fonksiyonu olarak kârı hesaplayabilmek için; Toplam Gelir (TG) fonksiyonu, birim satış fiyatının (f ) üretim veya satış miktarı (x) ile çarpılması sonucunda bulunur. Toplam maliyet fonksiyonu ise daha öncede belirtildiği gibi,

TM = ax + b şeklinde hesaplanmaktadır. Kâr fonksiyonunda belirtilen değerler yerine koyulduğunda satış miktarı cinsinden kâr formülü ise;

Kâr = (f-a)x – b olur. Sabit maliyeti karşılayan ve kâra katkıda bulunan kısım olan “katkı payı” kullanılarak formül yeniden ifade edilecek olursa

Kâr = (Katkı Payı x Satış Miktarı) – Toplam Sabit Maliyet

Kâr = KP x – b olur.

İşletmelerde, bazı durumlarda dönem kârının, satış miktarı yerine satış tutarının bir fonksiyonu olarak belirlenmesi gerekebilir. Bu durumda Satış tutarı cinsinden hesaplanan dönem kârı, katkı oranı yoluyla hesaplanır. Katkı oranı (KO), satılan her ürünün katkı payının birim satış fiyatına bölünmesiyle bulunur.

Katkı oranı ile ifade edilen dönem kârını aşağıdaki gibi ifade etmek olanaklıdır:

Kâr = (Katkı Oranı x Toplam Net Satışlar) – Toplam Sabit Maliyet
Kâr = KO x – b olur.

İşletmelerde kâr fonksiyonu aşağıda belirtilen şekillerde kullanılabilmektedir:

• Çeşitli Satış Hacimlerinde Sağlanacak Kârların Tahmini
• Hedef Kârı Sağlayan Satış Hacminin Belirlenmesi:
  • - Hedeflenen kârı sağlayan satış miktarının bulunması
  • - Hedeflenen kârı sağlayan satış tutarının bulunması
• Başabaş Noktası ve Başabaş Grafiğinin Belirlenmesi

Lojistik işletmelerinde gelecek yıllarda taşınacak mal miktarı tespit edilebilirse, kâr fonksiyonundan yararlanılarak gelecek yıllarda elde edilecek kâr tutarı da hesaplanabilir. Bu kâr tutarı yukarıda açıklanan hem satış miktarını esas alan kâr fonksiyonunda hem de satış tutarını esas alan kâr fonksiyonunda aynı tutarlara ulaşılacak şekilde hesaplanabilir.

Lojistik işletmeler kâr fonksiyonundan yararlanarak gelecekte hedefledikleri kâr için gerekli satış miktarını ve satış tutarını hesaplayabilmektedir. İşletmelerin hedefledikleri kâr ise, satış miktarı ve satış tutarını ele alan kâr fonksiyonunu satış hacmine eşitlenmek suretiyle hesaplanır.

Ticari işletmelerin kurulma nedeni kâr elde etmek ve işletmenin sürekliliğini sağlamaktır. Bu amaçla işletmeler hangi satış miktarı ve satış tutarında, ne kâr ne de zarar elde edeceğini bilmek ister. İşletmelerin toplam satış gelirleri ile sabit ve değişken giderler toplamının birbirine eşit olduğu bu nokta Başabaş Noktası ya da Kâra Geçiş Noktası olarak adlandırılır. Başabaş noktası analizi yapılırken aşağıdaki varsayımlar göz önünde bulundurulur. Bunlar;

• Giderler, sabit ve değişken olarak ikiye ayrılmalıdır.
• Birim başına değişken gider, taşıma miktarından bağımsız olarak sabit kalır.
• Birim satış fiyatı sabittir.
• İşletmenin tek ürünü taşıdığı kabul edilmektedir. İşletme, birden fazla ürün taşısa bile her ürünün toplam içindeki payı sabit kalmaktadır.
• Sabit giderler çeşitli üretim seviyelerinde aynı kalmaktadır.

Başabaş Noktasının Satış Miktarı Olarak Bulunması:

B.B.N. (Satış Miktarı) = b / KP

Başabaş Noktasının Satış Tutarı Olarak Bulunması:

B.B.N. (Satış Tutarı) = b / KO