Devre Analizi Dersi 6. Ünite Özet
Rl Ve Rc Devreleri
Giriş
Tek tip depolama elemanı (bobin veya kondansatör) ve direnç içeren RL ve RC devreleri birinci dereceden devreler olarak isimlendirilir. Bu devreler, RL devresinde bobin akımının, RC devresinde kondansatör voltajının değişken olarak tanımlandığı diferansiyel denklemlerle karakterize edilmektedir.
RC Devresi
RC devresi, direnç ve kondansatörden oluşan gerilim veya akım kaynağı tarafından beslenen bir elektrik devresidir.
Uzun süre bir DA akım veya gerilim kaynağı ile beslendikten sonra, herhangi bir t = t 0 anında anahtarlama ile kaynaklarla bağlantısı değişmiş RC devrelerinde anahtar konumu değişmeden önceki zaman diliminde kondansatör açık devre gibi davranır. Anahtarın konumu değiştikten sonra devrenin tüm bağımsız kaynaklarla ilişkisi kesilirse ortaya çıkan akım ve gerilim davranışına RC devresinin doğal tepkisi denir.
Şekildeki gibi RC anahtarlama devresinde, DA voltaj kaynağı tarafından uzun bir süre beslendikten sonra t = 0 anında anahtar açılmaktadır.
Anahtar kapalı konumdayken, DA voltaj kaynağı tarafından uzun süre beslenen kondansatör açık devre gibi davranır, üzerindeki voltaj sabit bir değere ulaşır ve zamana göre değişkenlik göstermez.
t < 0 için kondansatör üzerindeki akım:
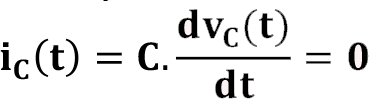
t < 0 için kondansatörün plakaları arasındaki potansiyel fark:
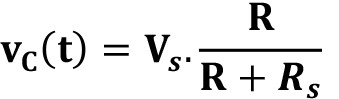
Anahtar t = 0 anında açıldığında, kondansatör voltajı ani olarak değişemeyeceğinden, kondansatörün t = 0 anındaki voltaj değeri çok kısa süre önceki ve sonraki değerini korur. Bu değer, doğal tepkinin hesaplanmasında kullanılacak başlangıç değeridir ve V C0 ile gösterilir:
V C0 = v C (0) = v C (0 + ) = v C (0 - )
Anahtar kapatıldıktan sonra t ? 0 için aktif devre, şekildeki gibi sadece direnç ve kondansatörden oluşan kaynaksız bir RC devresi haline gelir.
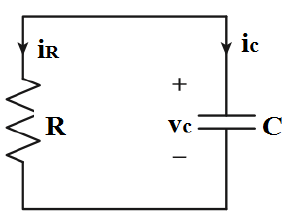
Kondansatörün doğal tepkisini ifade eden kondansatör voltaj değeri (t ? t 0 ):
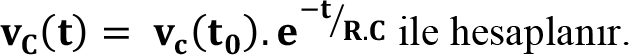
Burada v C (t 0 ), kondansatör voltajı için başlangıç değeridir ve v C (t 0 ) = V C 0 dır.
V C 0 = v C (0) eşitliği kullanılarak ifade şöyle de yazılır:
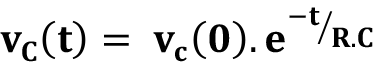
RC devresinin çözümündeki negatif üs değerine sahip exponansiyel terimdeki R.C ifadesi RC devresinin zaman sabitidir.  ile gösterilir, birimi sn’ dir.
ile gösterilir, birimi sn’ dir.
 =R.C
=R.C
RC devrelerinde birden fazla kondansatör veya direnç bulunması durumunda zaman sabiti hesaplanırken bu elemanların Thevenin eşdeğer bulma yöntemi kullanılarak elde edilen eşdeğerleri kullanılır. RC devrelerinde şarj/deşarj esnasında kondansatör enerjisinin %63 değişim göstermesi için gereken süre devrenin zaman sabitine eşittir.
Akım ve gerilim kaynaklarından bağımsız bir RC devresinde anahtarlamadan sonra yani t > 0 için RC devresinin doğal tepkisindeki kondansatör voltaj değeri, bu voltajın başlangıç değerine ve devrenin zaman sabiti parametrelerine bağlıdır.
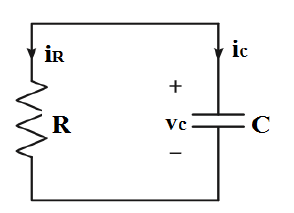
Kondansatör üzerinden geçen i C (t) akımı t >0 için şu şekilde hesaplanır:
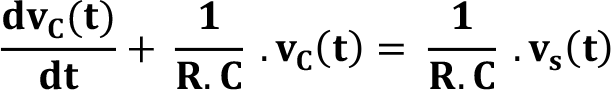
Şekilde t >0 için i C (t) + i R (t) olduğundan i C (t) = –i R (t) eşitliği elde edilir. Buna göre direnç üzerinden geçen akım:
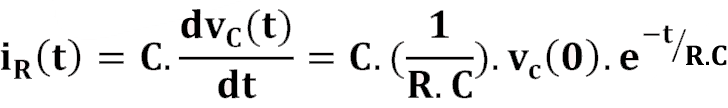
RL Devresi
RL devresi, direnç ve bobinden oluşan, gerilim veya akım kaynağı tarafından beslenen bir elektrik devresidir.
Uzun süre bir DA akım veya gerilim kaynağı ile beslendikten sonra, herhangi bir t = t0 anında anahtarlama ile kaynaklarla bağlantısı değişmiş RL devrelerinde anahtar konumu değişmeden önceki zaman diliminde bobin kısa devre gibi davranır. Anahtarın konumunun değiştirilmesinden sonra ise devrenin tüm bağımsız kaynaklarla ilişkisi kesiliyorsa ortaya çıkan akım ve gerilim davranışı RL devresinin doğal tepkisi olarak adlandırılır.
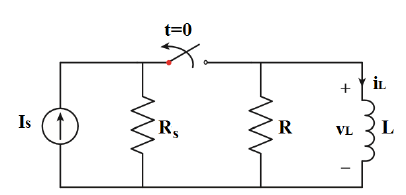
Şekildeki RL anahtarlama devresinde, DA voltaj kaynağı tarafından uzun bir süre beslendikten sonra t = 0 anında anahtar açılmaktadır.

DA akım kaynağı tarafından uzun bir süre beslenen bobin, anahtarın kapalı konumda bulunmasıyla, üzerinden geçen akım sabit bir değere ulaşır ve zamana göre değişkenlik göstermez.
t < 0 için bobin üzerindeki voltaj şu şekilde hesaplanır:
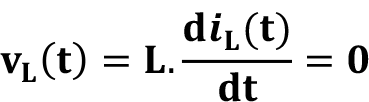
Buna göre bobine paralel bağlı R direnci üzerindeki gerilim ve akım değerleri de sıfır olduğundan t < 0 da bobin üzerinden geçen akım: i L (t) = I s dir.
Burada DA akım kaynağı ile beslenen ideal bobin, bir tel gibi davranır ve tüm akımı çeker.
Anahtar t = 0 anında açıldığında, bobin akımı ani olarak değişemez. Bu nedenle bobinin t = 0 anındaki akım değeri çok kısa süre önceki ve sonraki değerini korur. Bu değer doğal tepkinin hesaplanmasında kullanılacak olan başlangıç değeridir ve I L0 ile gösterilir.
I L0 = i L (0) = i L (0 + ) = i L (0 – )
Üzerinde enerji depolanan bir bobin için i L (0) ? 0 dır.
Anahtar açıldıktan sonraki aktif devre, şekildeki gibi sadece direnç ve bobinden oluşan kaynaksız bir RL devresidir.
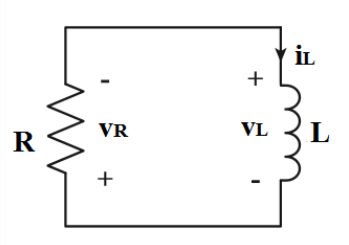
Bobinin doğal tepkisini ifade eden bobin akım değeri:

Burada i L (0), bobin akımı için başlangıç değeridir ve anahtarlamadan önce bobin üzerinden geçen akıma eşittir:
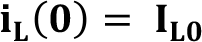 eşitliği kullanılarak ifade tekrar yazılırsa elde edilen eşitlik:
eşitliği kullanılarak ifade tekrar yazılırsa elde edilen eşitlik:
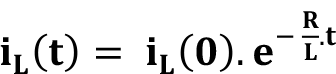
Denklemde negatif üs değerine sahip exponansiyel terim, bobinde depolanan enerjinin ve dolayısıyla akımın zaman geçtikçe sıfır değerine yaklaştığını ve başlangıç değerinin bir süre sonra akım değeri üzerindeki etkisini kaybettiğini göstermektedir. Bu sürenin uzunluğu devrenin zaman sabitine bağlıdır.
RL devrelerinde devre çözümündeki negatif üs değerine sahip exponansiyel terimin zaman katsayısının tersi, RL devresinin zaman sabitidir. RL devresinin zaman sabiti:
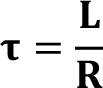
Akım ve gerilim kaynaklarından bağımsız bir RL devresinde anahtarlamadan sonraki (yani t ? 0 için RL devresinin doğal tepkisindeki) bobin akım değeri, bu akımın başlangıç değerine ve devrenin zaman sabiti parametrelerine bağlıdır. t >0 direnç üzerindeki gerilim:
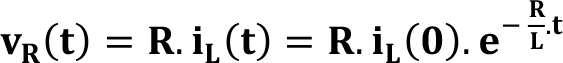
Şekilde v R (t) + v L (t) = 0 olduğundan v L (t) = –v R (t) eşitliği elde edilir. Bobin üzerindeki potansiyel fark t > 0 için iki şekilde hesaplanabilir:

RL devrelerinde birden fazla bobin veya direnç bulunması durumunda zaman sabiti hesaplanırken bu elemanların Thevenin eşdeğer bulma yöntemi kullanılarak elde edilen eşdeğerleri kullanılır.
Anahtarlama Fonksiyonları
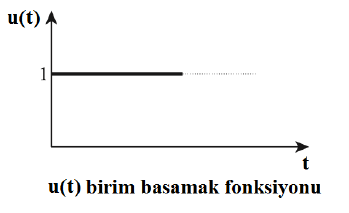
Birinci dereceden devrelerin ani olarak bir kaynak etkisine girmesi ile oluşan tepki zorlanmış tepkidir. Birinci dereceden devrelere ani bir kaynak bağlanması sonucunda devrenin analizini yapmak için kullanılan fonksiyonlara anahtarlama fonksiyonları denir. En çok kullanılan anahtarlama fonksiyonlarından biri de birim basamak fonksiyonu ’dur.
Genel birim basamak fonksiyonu u(t) ile gösterilir. u(t) fonksiyonu, t’nin negatif değerleri için 0, pozitif değerleri için 1’dir. t = 0 için ise tanımsızdır.
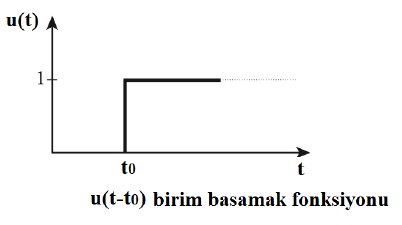
Genel birim basamak fonksiyonu zaman ekseninde t0 kadar sağa kaydırıldığında u(t – t0) birim basamak fonksiyonu elde edilir. u(t – t0) fonksiyonu t < t0 için 0, t > t0 için 1 değerini alır. t = t0 için ise tanımsızdır.
Elektrik devrelerinde, birim basamak fonksiyonu akım ya da gerilimdeki ani değişimleri ifade etmek için kullanılır
RL ve RC Devrelerinde Zorlanmış Tepki ve Tüm Tepki
Anahtarlamalı bir RL veya RC devresinde anahtar konum değiştirdikten sonra hala bir kaynakla bağlantı devam ediyorsa devrenin akım ve gerilim davranışı devrenin tüm tepkisi olarak adlandırılır. Bir başka ifade ile devrede oluşan doğal tepki ve zorlanmış tepkinin toplamı tüm tepki dir.
Şekildeki zorlanmış RC devresini karakterize eden denklem:
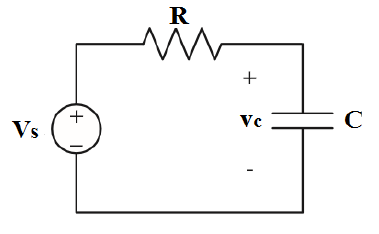
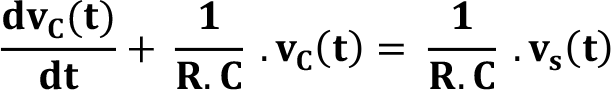
Denklemde 1 / R.C ifadesi RC devresinin zaman sabitinin tersini yani 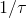 ’ yu göstermektedir.
’ yu göstermektedir.
Zorlanmış RL devresini karakterize eden denklem:
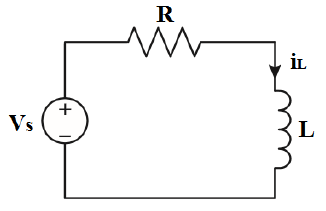
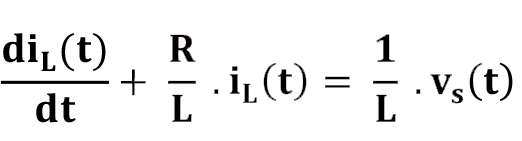
Denklemde R/L ifadesi RL devresinin zaman sabitinin tersini yani 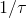 ‘yu ifade etmektedir.
‘yu ifade etmektedir.
Zorlanmış RC ve RL devrelerini karakterize eden diferansiyel denklemler ortak olarak şöyle yazılır:
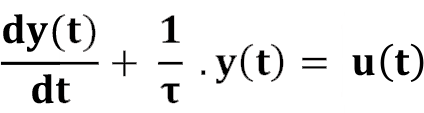
Denklemde:
?: devrenin zaman sabiti,
u(t): sistemin girdisi,
y(t): RC devreleri için kapasitör voltajı (v C (t)) ve RL devreleri için bobin akımıdır (iL(t)).
RC ve RL devrelerini karakterize eden diferansiyel denklemin çözümü genel olarak şöyle ifade edilir:

Bu denklem çözümü devrenin zorlanmış ve doğal tepkisini içerir, yani devrenin tüm tepkisidir. Denklemde K 1 ve K 2 katsayıları şu şekilde hesaplanır:
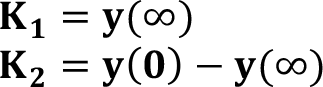
-
2025-2026 Bahar Dönemi Ara (Vize) Sınavı İçin Sınav Merkezi Tercihi
date_range 9 Gün önce comment 3 visibility 494
-
AÖF 2025-2026 Öğretim Yılı Bahar Dönemi Kayıt Yenileme Duyurusu
date_range 1 Şubat 2026 Pazar comment 3 visibility 321
-
2025-2026 Öğretim Yılı Güz Dönemi Ara (Vize) Sınavı Sonuçları Açıklandı!
date_range 16 Aralık 2025 Salı comment 5 visibility 825
-
2025-2026 Güz Dönemi Dönem Sonu (Final) Sınavı İçin Sınav Merkezi Tercihi
date_range 3 Aralık 2025 Çarşamba comment 3 visibility 813
-
2025-2026 Güz Dönemi Ara (Vize) Sınavı Sınav Bilgilendirmesi
date_range 2 Aralık 2025 Salı comment 2 visibility 668
-
Başarı notu nedir, nasıl hesaplanıyor? Görüntüleme : 26803
-
Bütünleme sınavı neden yapılmamaktadır? Görüntüleme : 15411
-
Harf notlarının anlamları nedir? Görüntüleme : 13583
-
Akademik durum neyi ifade ediyor? Görüntüleme : 13379
-
Akademik yetersizlik uyarısı ne anlama gelmektedir? Görüntüleme : 11159