Fotogrametri Dersi 2. Ünite Özet

Tanımlar

Çerçeve İşaretleri: Fotogrametrik kameralarla çekilmiş fotoğrafların köşelerinde veya kenar ortalarında bulunan özel işaretlerdir. İç yöneltmede kullanılan bu işaretlere çerçeve işaretleri ya da fotoğraf orta nokta bulucuları denir.

Fotoğraf Orta Noktası (Orta Nokta): Çerçeve işaretlerinin karşılıklı olarak birleştirilmesi ile elde edilen kesim noktasına denir.

İzdüşüm Merkezi (O): Kamera optik sisteminin merkezine izdüşüm merkezi denir.

İzdüşüm Işını (POP'): Nesne uzayındaki bir noktadan gelen ve izdüşüm merkezinden geçerek P' fotoğraf noktasını oluşturan doğru parçasıdır.

Kamera Ekseni: Kamera optik sisteminin eksenine kamera ekseni veya asal eksen denir.

Asal Nokta: İzdüşüm merkezinden fotoğraf düzlemine indirilen dikin ayağıdır. Bu nokta fotoğraf orta noktasının çok yakınındadır. Bu nokta aynı zamanda kamera ekseninin fotoğraf düzlemini ve nesne yüzeyini deldiği H ve H' noktasıdır.

Asal Uzaklık (c= 0H'): Fotoğraf düzlemi ile izdüşüm merkezi arasındaki uzaklıktır. Bu uzaklık net görüntünün oluştuğu fotoğraf düzlemi ile mercek arasındaki uzaklıktır. Yani fizik derslerinde adlandırıldığı şekliyle görüntü uzaklığıdır.

Ayakucu (Nadir) Noktası (N-N'): İzdüşüm merkezinden geçen çekül doğrusu fotoğraf ve araziyi ayakucu noktasında keser.

Düşey Fotoğraf: Kamera ekseni düşey konumda iken çekilen fotoğrafa denir ( g =0 ⁰ ). Pratikte tam düşey fotoğraf çekilemez. Bu nedenle g ?5 ^o olan fotoğraflara düşey fotoğraf denir.

Yatay Fotoğraf: Kamera ekseni yatay konumda iken çekilen fotoğrafa denir ( g = 90 ⁰ ).

Işın Destesi: İzdüşüm merkezinden geçen tüm izdüşüm ışınları kümesine denir.

Işın Demeti: İzdüşüm merkezinden geçen ve bir düzlem içinde bulunan izdüşüm ışınları kümesi.

İç Yöneltme Elemanları: Fotogrametrik kameraların asal uzaklığı ile asal noktasının konumuna iç yöneltme elemanları denir. Asal noktanın konumu, çerçeve işaretlerinin oluşturduğu koordinat sistemine göre tanımlanır. Bu üç eleman, yani c ve x ⁰ , y ⁰ ışın destesinin yeniden oluşturulmasında ya da tanımlanmasında gerekli olmaktadır.

Geometrik Temeller/ Fotoğraf Geometrisi

Üç boyutlu uzaydaki noktalar iki boyutlu bir uzaya, yani bir düzleme geometrik bir yöntemle aktarılabilir. Üç boyutlu uzaydaki noktaların bir düzleme geometrik bir yöntemle aktarılmasında üç tür izdüşüm söz konusudur:

1. Paralel izdüşüm: Bir d doğrusuna paralel izdüşüm doğruları çizerek izdüşüm düzlemini deldiği noktalar bulunur.
2. Dik (Ortogonal) izdüşüm: Noktalardan izdüşüm düzlemine dikler inilir. Bu noktalar nesnenin izdüşüm noktalarıdır. Harita, dik bir izdüşümdür. İzdüşüm düzlemi olarak yeryüzünün belirli bir noktasına teğet olan bir düzlem alınır. Genellikle bu düzey deniz yüzeyine paralel bir düzlemdir ve dik izdüşüm küçültülerek kâğıda aktarılır.
3. Merkezsel izdüşüm: Uzay noktaları izdüşüm düzlemi dışındaki bir O noktası ile birleştirilir. Bu doğruların düzlemi deldiği noktalar ilgili noktaların merkezsel izdüşümüdür. O noktası izdüşüm merkezidir.

Fotoğraf merkezsel bir izdüşüm olduğuna göre, merkezsel izdüşümün bütün özellikleri aynı zamanda fotoğrafın geometrik özellikleridir. Bu özelliklerin bazılarını aşağıdaki gibi ifade edebiliriz.

• Üç boyutlu bir uzaydaki bir P noktasına karşılık izdüşüm düzleminde tek bir P' noktası vardır. İzdüşüm düzlemindeki bir P' noktasına OP izdüşüm ışını üzerinde, sonsuz sayıda nokta karşılık gelir.
• Üç boyutlu uzaydaki bir d doğrusuna karşılık izdüşüm düzleminde bir tek d' doğrusu vardır. İzdüşüm düzlemindeki bir d' doğrusuna d doğrusu ve O izdüşüm merkezinin belirlediği düzlem üzerinde sonsuz sayıda doğru parçası karşılık gelir.
• Uzayda birbirine paralel olan fakat izdüşüm düzlemine paralel olmayan doğruların izdüşümleri kesişir. İzdüşüm düzlemine paralel olan birbirine paralel doğrular izdüşüm düzleminde de birbirine paralel kalır. Paralel doğruların izdüşüm düzlemindeki kesişme noktasına kaçış noktası denir. Kesişen doğrular izdüşümde de kesişir. Kesişme noktaları birbirine karşılık gelir.
• Bir doğru üzerinde bulunan dört nokta için yazılacak bir çifte oran, merkezsel izdüşümde değişmez kalır. Buna çiftte oran özelliği denir. Merkezsel izdüşümde, bu özellik yardımı ile doğru demetleri arasında da bir ilişki kurulabilir. Bilinen üç doğrultu yardımı ile fotoğrafta bulunan dördüncü bir doğrultunun nesne uzayındaki ya da haritadaki karşılığı bulunabilir.

Merkezsel izdüşümün ilk iki özelliği, tek bir merkezsel izdüşümle üç boyutlu bir uzayın noktalarının bulunamayacağı anlamına gelir. Ancak iki boyutlu bir uzayın (bir düzlemin) merkezsel izdüşümü söz konusu ise yukarıdaki iki özelliğin tersleri de geçerlidir. Yani izdüşüm düzlemindeki bir noktaya karşılık bir nokta, bir doğru parçasına karşılık da bir doğru parçası gelir. Bu irdelemeler sonucu, fotogrametri için önemli olan şu sonuçlar çıkmaktadır:

• Tek bir fotoğraftan ölçme uzayındaki noktaların X,Y,Z koordinatları elde edilemez.
• Ölçme uzayındaki noktalar bir düzlemde bulunuyorsa, ölçüm için bir tek fotoğraf yeterlidir.
• Ölçüm uzayındaki noktaların konumlarının, yani X,Y,Z koordinatlarının bulunması için başka bir noktadan çekilmiş ikinci bir fotoğraf gereklidir. Böylece aynı noktaya ait iki izdüşüm ışını nesne noktasında kesiştirilebilecektir.

Matematik Temeller

Uluslararası Fotogrametri Birliği (International Society for Photogrammetry) 1960 yılında Londra’da yaptığı kabulle fotogrametrik çalışmalarda kullanılacak koordinat sistemleri hakkında bir standart oluşturmuştur. Bu açıklamaya göre, fotogrametride kullanılan formül ve türetmeler aşağıda tanımlanan koordinat sistemlerine göre yapılmalıdır.

Fotoğraf Koordinat Sistemi

Eksenleri cisim koordinat sistemiyle aynı yönde olan ve sağ el koordinat sistemine uyan xyz koordinat sistemidir. Başlangıç noktası O izdüşüm merkezidir. xy düzlemi fotoğraf düzlemine paralel, z ekseni de kamera ekseni ile çakışıktır. x ekseni komşu fotoğrafın izdüşüm merkezi doğrultusundadır. Bu yön hava fotogrametrisinde, yaklaşık olarak uçuş çizgisi doğrultusudur. Noktaların z koordinatı sabit ve asal uzaklığa eşittir. Bu nedenle, bu koordinat sistemi fotoğraf düzleminde ve iki boyutlu olarak düşünülürse, bu koordinat sisteminin de başlangıç noktası asal noktadır.

Uzay Koordinat Sistemi

Fotogrametride nesne uzayındaki noktalar uzay koordinatları ile tanımlanır. Uzay koordinat sistemi, X ekseni pozitif yönü uçuş yönü doğrultusunda (hava fotogrametrisi için), Z ekseni XY düzlemine dik ve sağ el koordinat sistemine uyan dik bir XYZ koordinat sistemidir. Başlangıç noktasının seçimi serbesttir. Ancak Z (H) ekseni her durumda düşey doğrultuda, XY düzlemi de her zaman yatay bir düzlemdir.

Koordinat Dönüşümü

İki ayrı koordinat sistemindeki nokta kümelerinin, bir sistemdeki koordinatlarının diğer sisteme dönüştürülmesi işlemine “Koordinat Dönüşümü (Transformasyon)” denilmektedir. Bu işlemi gerçekleştiren formüllere de dönüşüm formülleri denir. Dönüşüm formüllerinde geçen parametreler biliniyorsa, bir sistemde koordinatları verilen bir noktanın diğer bir sistemdeki koordinatları kolayca bulunur. Genellikle dönüşüm parametreleri bilinmez, her iki sistemde de koordinatları bilinen ortak noktalar yardımıyla parametreler hesaplanır.

İki Boyutlu Benzerlik Dönüşümü: Benzerlik dönüşümünde geometrik şekillerin benzerliği korunur. Düzgün geometrik şekillerin kenarları aynı oranda küçülür ya da büyür. Açıların mutlak değerleri değişmez kalır. Şekiller dönüşümden sonra esas şekle benzerler. İki koordinat sistemi arasında bir ? ölçek katsayısı söz konusu ise ve başlangıçları da farklı ise aşağıdaki gibi genel bir dönüşüm formülü yazılabilir

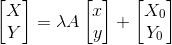
Buna göre benzerlik dönüşümünde 1 ölçek, 1 dönüklük ve 2 öteleme olmak üzere toplam 4 parametre vardır. Çözüm için her iki sistemde koordinatları bilinen iki nokta gereklidir. İkiden fazla ortak nokta olması durumunda dönüşüm parametreleri en küçük kareler yöntemine göre dengeleme ile hesaplanır.

İki koordinat sistemi arasındaki dönüşüm parametrelerinin bulunması için, her iki sistemde de koordinatları bilinen, iki ortak noktaya ihtiyaç duyulur. P1 ve P2 noktalarının 1. koordinat sistemindeki koordinatları sırasıyla (x ₁ , y ₁ ) ve (x ₂ , y ₂ ), 2. koordinat sistemindeki koordinatları (X ₁ , Y ₁ ) ve (X ₂ , Y ₂ ) olsun. P1 ve P2 noktaları için dönüşüm denklemleri aşağıdaki gibi yazılır.

X ₁ = ax ₁ - by ₁ + c (1)

Y ₁ = bx ₁ + ay ₁ + d (2)

X ₂ = ax ₂ - by ₂ + c (3)

Y ₂ = bx ₂ + ay ₂ + d (4)

İki Boyutlu Affin Dönüşümü: Jeodezide genellikle benzerlik dönüşümü kullanılmasına rağmen fotogrametri ve kartoğrafyada durum farklıdır. Film, kâğıt vb. maddeler deformasyona uğradıkları zaman her iki eksen boyunca bozulmalar aynı olmaz. Bu durumda Affin dönüşümü tercih edilir. Bu dönüşümde koordinat eksenleri yönündeki ölçekler aynı değildir. Uzunluklar yöne bağlı olarak değişir. Belirli bir yönde ölçek değişmez kalır. Açılar dönüşümden sonra değişir. Açıların değişimi açı kollarının doğrultusuna bağlıdır. Açı koruyan bir dönüşüm değildir. Herhangi bir doğru dönüşümden sonra yine bir doğrudur. Paralel doğrular dönüşümden sonra da paraleldir. Alanlar dönüşümden sonra sabit bir miktar kadar değişir. Bu sabit miktar dönüşüm matrisinin determinantına eşittir. Bir kare, affin dönüşümü sonucu paralel kenara dönüşmektedir. Fotogrametride bazı problemlerin çözümünde dört parametreli benzerlik dönüşümü yerine altı parametreli bir dönüşüm uygulanır. Affin dönüşümü adı verilen bu dönüşümde altı parametre, x ve y eksenleri yönünde 2 ölçek faktörü, 2 dönüklük ve 2 ötelemedir. Affin dönüşümünün benzerlik dönüşümünden temel farkı her iki eksen yönündeki ölçek faktörlerinin ve dönüklük açılarının farklı olmasıdır. Affin dönüşümünde iki koordinat sistemi arasındaki ilişki şu eşitlik ile ifade edilir:

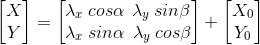
Üç Boyutlu Koordinat Dönüşümü: Başlangıçları aynı olan iki üç boyutlu dik koordinat sistemi arasındaki dönüşüm formülleri aşağıdaki gibi yazılabilir:

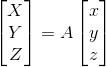
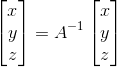
Dönüşüm Matrisi (Ortogonal Matris)

Dönüşüm formüllerindeki l A dönüşüm matrisi uzunlukları l katsayısı oranında değiştirir. Ancak bu durumda şeklin benzerliği değişmez, açılar aynı kalır. Bu nedenle bu dönüşüme benzerlik dönüşümü denir. l = 1 durumunda dönüşüm özel bir dönüşümdür ki buna ortogonal dönüşüm denir. Ortogonal dönüşümde açılar ile birlikte uzunluklar da korunur. Fotogrametride sembolik olarak tanımlanan A dönüşüm matrisi ortogonal bir matristir. Ortogonal bir matrisin özelliklerini aşağıdaki gibi ifade edebiliriz.

• Ortogonal matrisin tersi transpozesine eşittir.
• Matrisin kendisiyle çarpımı 1’e eşittir.
• Her satırdaki ve sütundaki elemanların karelerinin toplamı 1’e eşittir.
• İki satır, ya da iki sütundaki elemanların karşılıklı olarak çarpımlarının toplamı sıfıra eşittir.
• Her eleman kendisinin kofaktörüne eşit ya da ters işaretlisidir.

Bu üç özellikten toplam 21 eşitlik yazılabilir. Bu eşitlikler incelenirse, bunların yalnız 6 tanesinin bağımsız olduğu, geriye kalan 15 denklemden 6 eşitliğin çıkarılabileceği görülür. Ortogonal matrisin 9 elemanı bulunduğu ve bu 9 parametre arasında birbirinden bağımsız 6 bağıntı yazılabileceğine göre bu matris uygun seçilecek 3 bağımsız parametre ile ifade edilebilir. Fotogrametride, bu üç bağımsız parametre olarak üç eksen çevresindeki dönüklük açıları alınır.

Dönüklük Açıları ve Dış Yöneltme Elemanları

Ortogonal matrisin üç bağımsız parametresi için, fotogrametride üç eksen çevresindeki dönüklük açılarının kullanıldığı ifade edilmişti. O izdüşüm merkezinden, XYZ uzay koordinat sisteminin eksenine paraleller çizilsin, böylece elde edilen xyz koordinat sistemi ve bu eksenler etrafında dönüklük açıları yardımı ile xyz fotoğraf koordinat sistemi, sanal uvw eksen sistemine göre tanımlanabilir. Sanal uvw eksen sisteminin yerine bu dönüklüklerin XYZ uzay koordinatları sisteminin eksenleri çevresindeki dönüklükleri gibi düşünmek daha uygundur.

Ortogonal Matrisin Dönüklük Açıları ile İfadesi

Fotoğraf koordinat sisteminin arazi koordinat sistemine göre dönüklüğünü ifade eden A matrisi, her biri ortogonal olan ve düzlem dönüklükten elde edilen üç matrisin arka arkaya çarpılmaları ile elde edilen bir matristir. A w , A j , A k ’ya kısmi dönüklük matrisleri denir. Matris çarpımlarında sıra önemlidir. Benzer şekilde, uzayda üç eksen çevresinde dönüklüklerin mekanik olarak gerçekleştirilmesinde de bir sıralama gereklidir. A w , A j , A k ’ya kısmi dönüklük matrislerinin arka arkaya çarpılmaları ile aşağıdaki dönüklük matrisi elde edilir.

İzdüşüm Denklemleri

Tam düşey hava fotoğrafı için elde edilen denklemlere izdüşüm denklemleri denir. Bu özel durum yerine genel durum göz önünde bulundurulursa, yani bu iki koordinat sistemi arasındaki ölçek farkı, dönüklük ve öteleme dikkate alınırsa, genel bir üç boyutlu benzerlik dönüşümü denklemini yazabiliriz.