Coğrafi Bilgi Sistemlerine Giriş Dersi 4. Ünite Özet
Temel Ölçme Aletleri Ve Haritacılık Hesapları
Basit Ölçme Aletleri
Ölçme işlemlerinde kullanılan aletler aşağıdaki Jalon, Jalon Sehpası, Çekül, Çelik Şerit Metre, Alet Sehpası, Total Station, Nivo ve Mira ve GPS’dir.
Arazide harita yapımında kullanılan ve zemine gömülü haldeki noktalara nirengi veya poligon denir. Beton bloklarla ya da boru, çivi vb. şekillerde işaretlenen bu noktaların uzaktan görülebilmesi ve ölçüm yapılabilmesi için kullanılan ölçme araçlarına Jalon denir. Jalonun ucunda sivri bir demir bulunur, 2 metre boyunda 3-4 cm çağında demirden yapılmıştır ve uzaktan rahatlıkla görülebilmesi için her 50cm’si farklı renklerle (beyazkırmızı) boyanmıştır. Aplikasyon, daha önceden yapılan imar projeleri ve benzeri gibi projelerin zemine uygulanması işine denir. Jalonlar genelde geçici noktaların belirlenmesinde, doğrultuya girmede, aplikasyon ve alım yapmada kullanılırlar. Jalon kendi ekseni etrafında döndürüldüğünde yalpalıyorsa arızalıdır.
Beton gibi sert zeminlerde jalonu saplamak mümkün olmadığından zemin üzerinde dik konumda durabilmesi içi üç ayaklı demir Jalon sehpaları kullanılır.
Bazen şakül olarak da adlandırılan ve bir noktanın düşey olarak iz düşümünün bulunmasında veya jalonun düşey konuma getirilmesinde çekül, demir bir ağırlık ve ona asılı olarak duran bir ipten oluşur. Çekülün rüzgardan etkilenmemesi için ağır olması tercih edilir.
10, 20, 30 veya 50 metre uzunlukta olabilen çelik şerit metre genellikle mesafe ölçümlerinde sıklıkla kullanılan bir alettir ve ölçümlerde kolaylık olması açısından genellikle 20 metrelik çelik şerit metreler kullanılır. Çelik şerit metreler genellikle 20o C sıcaklıkta ayarlandıklarından bu sıcaklığın altında veya üstündeki sıcaklık değerlerinde ölçüm yapıldığında aletin kullanım kılavuzundaki düzeltme değerleri esas alınarak düzeltme işleminin yapılması gerekir.
Total Station, Nivo gibi cihazların belli bir nokta üzerine kurulmasında kullanılan alet sehpalarının üç ayağı ve bu ayakların uçları olan sivri pabuçlar toprağa girecek şekilde bastırılarak toprağa girmesi sağlanır.
Hassas uzunluk ve açı ölçme amacıyla kullanılan total station ana ünite kontrol ünitesi olan klavyeden oluşan ve düzeçlenerek kullanılması gereken bir cihazdır. Düzeçleme işlemi altında bulunan ayar vidaları ile yapılan total station cihazlarının içinde WindowsCE işletim sistemi bulunmaktadır.
Gelişmiş cihazlar ile reflektörsüz ölçüm yapma imkanı olan total station cihazları normalde reflektör adı verilen ve jalon üzerine takılan bir aparat ile ölçüm yaparlar.
Reflektör gelen ışığı aynı şekilde yansıtan bir aparattır. Böylece elektronik bir cihaz ile ölçüm yapılacağı zaman ışığın geliş ve gidiş zamanı ölçülerek aradaki mesafe otomatik olarak kolayca hesaplanır.
Hassas yükseklik ölçümünde sıklıkla kullanılan Nivo cihazlarında aynı su terazisinde olduğu gibi bir silindirik düzeç mevcuttur ve bu düzeç sayesinde Nivo cihazının yataylığı sağlanır. Nivo cihazları yatay eksende istenildiği kadar döndürülebilir, ancak düşey eksende döndürülemez. Nivo yatay açı okunmasında da kullanılabilir.
Yükseklik ölçmelerinde Nivo cihazı ile birlikte kullanılan Mira, üzerinde metre-santimetre bölümleri bulunan ve fırınlanmış ağaçtan veya alüminyumdan yapılan bir malzemedir. Nivo ile ölçüm yaparken, ölçüm yapılacak noktaya mira ile bir kişi gider ve mirayı düzeçli bir şekilde tutar, Nivonun başında duran teknisyen ise okumayı gerçekleştirir. Teknolojinin gelişmesiyle birlikte elektronik Nivolar kullanılmaya başlanmıştır. Bu sistemde, mira üzerinde tıpkı barkod sistemi gibi işaretlenmiş simgeler vardır. Bu sistemde direk okuma yapılır ve okunan değer Nivonun içerisindeki hafızaya kayıt edilir. Ofis ortamında bu veriler kolayca bilgisayar ortamına aktarılabilirler.
GPS
GPS (Global Positioning System = Küresel Yer Belirleme Sistemi ya da Küresel Konumlandırma Sistemi ) her türlü hava şartlarında, gece-gündüz, 365 gün, 24 saat çalışabilen ve dünya üzerinde konumumuzu belirlemeye çalışan; yoğun ağaçlı alanlar, yüksek gerilim hatları vb. problemler dışında çok iyi performansla çalışan cihazlardır.
Sayısal harita, bilgisayar ortamlarında dosya ve veritabanı şeklinde saklanabilen haritalardır. Bunlar vektör, raster ve matris haritaları şeklinde üçe ayrılırlar. Sayısal haritaların geliştirilmesiyle birlikte, özellikle 911 gibi içerisinde farklı disiplinlerden meslek gruplarını barındıran (polis, itfaiye, sağlık vb.) teşkilatlar kendi araçlarının yerlerini bu cihazlar vasıtasıyla bulup en kısa ve hızlı yoldan olay yerine yönlendirmekte, seyrüsefer amaçlı kullanımı yaygınlaşmaktadır ve hatta bazı otomobil firmaları araçlarında bu imkanı standart donanımlarının içine eklemeye başlamışlardır.
GPS sistemleri aşağıdaki üç bölümden oluşmaktadır:
- Uzay Bölümü(Uydular)
- Kontrol Bölümü(Yer istasyonları)
- Kullanıcı Bölümü(GPS alıcısı)
Uzay bölümü (uydular); Dünya yüzeyinden yaklaşık olarak 20.000 km yükseklikte bir yörüngeye konumlandırılmış en az 24 uydudan (21 aktif uydu ve 3 yedek) oluşan bir sistemdir. Bu kadar yüksek mesafede bulunan uydular, Dünya üzerinde geniş bir görüş alanına sahiptirler. Bir GPS alıcısının koordinatları belirleyebilmesi için en az 4 uyduyu görmesi gerekmektedir
Kontrol Bölüm (yer istasyonları); GPS uydularını sürekli olarak kontrol ederek doğru yörünge ve zaman bilgilerinin GPS alıcılarına yayılmasını sağlarlar. 4 adedi insansız, 1 adedi insanlı olarak ana kontrol merkezini meydana getiren, Dünya üzerinde toplam 5 istasyon vardır.
Kullanıcı bölümü (GPS alıcısı); yerdeki alıcıları ifade etmektedir. Dünya üzerindeki konumunu farklı amaçlar için kullanan herhangi bir kişi sistemin kullanıcı bölümünü teşkil eder.
Dik Koordinat Sistemi ve Temel Ödevler
Bir düzlem içerisinde bulunan noktaların birbirlerine olan konumlarını belirlemek için kullanılan ve birbirlerini dik açı altında kesen iki doğrunun oluşturduğu sisteme “Dik Koordinat Sistemi” denir.
Koordinat eksenlerinin kuzey yönü “+X”, güney yönü “X”, doğu yönü “+Y”, batı yönü “-Y” olarak, eksenlerin kesişim noktasına orijin (başlangıç) noktası, X yönü apsis, Y yönü ordinat olarak adlandırılmaktadır. Bir noktanın apsis ve ordinatı o noktanın koordinatını tanımlamaktadır.
Matematik ve trigonometrik hesaplarda kullanılan koordinat sistemleri haritacılık hesaplarında kullanılmazken sağa ve sola giden eksen “X”, yukarı ve aşağı giden eksen “Y” olarak adlandırılır.
Yatay ve düşey eksenler ile dört bölüme ayrılan ve yarıçapı 1 birim olan daire trigonometrik dairedir. Trigonometrik dairede bölgeler saat ibresinin hareketinin ters istikametinde büyürken; jeodezik dairede saat ibresi hareketi ile aynı istikamette büyür.
Dik koordinat sisteminin oluşturduğu bir düzlemde, herhangi bir doğrunun +X ekseni ile oluşturduğu açıya açıklık açısı denir
Haritacılıkta çok sık karşılaşılan bazı hesap problemlerine temel ödevler denir. Çözümünde belli formüller ve hesaplamalar kullanılan temel ödevler bilinenler yardımıyla bilinmeyenlerin bulunması esasına dayanır.
Birinci temel ödev, bir A noktasının koordinatları (X a , Y a ), A noktasından B noktasına olan mesafe (AB=s), AB doğrusunun açıklık açısı (AB) bilinirken; bu bilinenler yardımıyla B noktasının koordinatlarının (X b , Y b ) hesaplanması esasına dayanan temel ödevdir
İkinci temel ödev, bir AB doğrusunun A ve B noktasının koordinatları (X a , Y a , X b , Y b ) bilinirken; AB doğrusunun açıklık açısı (AB) ve AB arasındaki mesafenin (s) hesaplanmasıdır.
Alan Hesapları
Arazi ölçümlerinin, çizilen haritalar ve planlar yardımıyla parsellerin ve istenilen sahaların alanları hesaplanabilir. Alan hesapları alım şekline ve istenilen hassasiyete göre değişir. Alan hesapları aşağıdaki dört şekilde yapılmaktadır:
- Ölçü değerlerine göre alan hesabı
- Ölçü ve plan değerlerine göre alan hesabı
- Plan değerlerine göre alan hesabı
- Planimetre ile alan hesabı
Planimetre, harita üzerindeki alanların bulunmasında kullanılan bir cihazdır.
Bahsedilen yöntemlerden en uygunu olan ölçü değerlerine göre hesap yönteminde alan hesabında hata olarak sadece ölçü değeri etki eder. Diğer üç yöntemde alanın ölçekli olarak çizilmesi gerekmektedir.
Bağlama yöntemi kullanılarak yapılan ölçü alım sonucunda belirlenen parselin alanı, üçgen alanlara ayrılır, her bir üçgen için yapılan alan hesabından sonra tüm üçgen alanları toplandıktan sonra arazinin alanı bulunmuş olur. Üç kenarı belli olan üçgene ait alan hesabı aşağıdaki formüllerle yapılır:
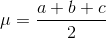
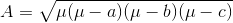
Alımın dik koordinat yöntemiyle yapıldığı durumda alan hesabı yapmak için üçgen ya da yamuk alanlardan yararlanılır.
Alım kutupsal yöntem kullanarak yapılmış ise; parselin alanının hesabı iki kenarın ve aralarındaki açının belli olduğu üçgenin alanının hesabından yararlanarak yapılır.
Hacim Hesapları
Büyük inşaatlarda, yol inşaatlarında, kanal çalışmalarında kazılacak ve dolgu yapılacak toprak miktarının hesaplanmasında aşağıdaki ölçülerden faydalanılarak hacim hesapları yapılır:
- Enkesitler
- Yüzey nivelman ölçüleri
Enkesit, yol projelerinde belirli noktalarda yolun enine kesilerek profilin çıkarılması işidir. Enkesitlerde yarma ve dolgu alanları bulunur.
Yüzey nivelmanı, hacmi hesaplanacak alanda karelaj oluşturularak köşe noktalarının yükseklik değerlerinin bulunması işidir.
Genelde dolgu veya yarma kesitli olan enkesit alanlar kullanılarak iki yarma veya dolgu kesiti arasındaki hacim aşağıdaki gibi hesaplanabilir:
A1: 1. Kesit Alanı
A2: 2. Kesit Alanı
t: İki kesit arasındaki mesafe
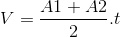
Arka arkaya gelen üç kesit arasındaki mesafe(t) eşit ise bu üç kesit için hacim hesabı Simpson formülü kullanılarak aşağıdaki gibi yapılır:
A i : İlk enkesit alanı
A m : Ortadaki enkesit alanı
A s : Son enkesit alanı
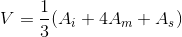
Birçok kesit olması durumunda ise hacim aşağıdaki şekilde hesaplanır:
A m : İlk ve son kesitler dışındaki ortada kalan enkesitlerin aritmetik ortalaması
N: İlk ve son enkesit dışındaki enkesit sayısı
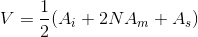
Bir enkesitte hem dolgu hem de yarma olursa yarma ve dolgu bölgesinin mesafesi olan x aşağıdaki gibi hesaplanabilir:
A y : Yarma kısmın alanı
A d : Dolgu kısmın alanı
t: Toplam enkesit genişliği
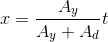
Yüzey nivelmanında arazi üçgen, kare veya dikdörtgenlerden oluşan kafeslere ayrılır. Verilen taban kotlarına göre kare veya dikdörtgen prizmalardan yararlanarak hacimler hesaplanır.
Üçgen prizmanın hacmi aşağıdaki gibi hesaplanır:
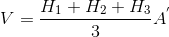
Dörtgen prizmanın hacmi aşağıdaki gibi hesaplanır:
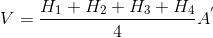
Kare prizmanın hacmi aşağıdaki gibi hesaplanır:
H R : Dış köşe yükseklikleri
H S : Dış kenar yükseklikleri
H İ : İç Yükseklik
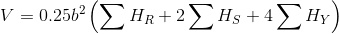
Karelaj yöntemi kullanılarak yüzey nivelmanı yapılmış arazinin ortalama arazi kotundan yararlanarak belirli bir kota kadar kazılacak toprak hacmi aşağıdaki gibi hesaplanabilir:
R: Dış köşe yükseklikleri sayısı
S: Dış kenar yükseklikleri sayısı
İ: İç yükseklikleri sayısı
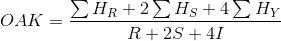
Verilen bir taban kotuna (T) kadar kazılacak toprak hacmi, A alanı için aşağıdaki formülle bulunur:
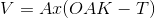
-
2025-2026 Bahar Dönemi Ara (Vize) Sınavı İçin Sınav Merkezi Tercihi
date_range 11 Şubat 2026 Çarşamba comment 4 visibility 1372
-
AÖF 2025-2026 Öğretim Yılı Bahar Dönemi Kayıt Yenileme Duyurusu
date_range 1 Şubat 2026 Pazar comment 1 visibility 678
-
2025-2026 Öğretim Yılı Güz Dönemi Ara (Vize) Sınavı Sonuçları Açıklandı!
date_range 16 Aralık 2025 Salı comment 3 visibility 1162
-
2025-2026 Güz Dönemi Dönem Sonu (Final) Sınavı İçin Sınav Merkezi Tercihi
date_range 3 Aralık 2025 Çarşamba comment 1 visibility 1159
-
2025-2026 Güz Dönemi Ara (Vize) Sınavı Sınav Bilgilendirmesi
date_range 2 Aralık 2025 Salı comment 1 visibility 949
-
Başarı notu nedir, nasıl hesaplanıyor? Görüntüleme : 26908
-
Bütünleme sınavı neden yapılmamaktadır? Görüntüleme : 15497
-
Harf notlarının anlamları nedir? Görüntüleme : 13759
-
Akademik durum neyi ifade ediyor? Görüntüleme : 13439
-
Akademik yetersizlik uyarısı ne anlama gelmektedir? Görüntüleme : 11217