Karar Modelleri Dersi 4. Ünite Özet
Karar Ağacı Ve Bayes Teoremi
Giriş
Karar mekanizmalarında, olasılıkların araştırmacılar tarafından belirlenmesi sürecinde, araştırmacıların olasılık algılarının değişkenlik göstermesi bazı durumlarda karar vericileri yanlış yönlendirebilmektedir. Herhangi bir karar probleminde başarısız olma olasılığının gerçek değerinden daha düşük belirlenmesi probleme ilişkin yeterli önlemlerin alınmasını engelleyebilir. Tersine başarısızlık olasılığının olduğundan daha yüksek belirlenmesi ise yüksek maliyetli tedbirlerin alınması sonucunu doğurabilecektir. Tecrübeler ve sezgilerin gerçek olasılık değerlerinden sapmasının nedeni; insanların belki de birbiriyle az ilişkili veya belki de birbiriyle hiç ilişkisi olmayan olayları birbirine uyumlu olarak yakıştırmasıdır. Diğer bir ifadeyle, bu tür olayların bir neden sonuç ilişkisi içinde olduğunu düşünerek yanılmalarıdır. Bir karar probleminde ayrıntılar arttıkça her bir ayrıntının gerçekleşme olasılığı azalır.
Ayrıntıların fazla olduğu karar problemlerinin çözümünde grafiksel veya görsel yaklaşımları benimsemek karar vericinin işini kolaylaştıracaktır. Karar problemlerinin çözümünde kullanılan geleneksel grafiksel teknik, karar ağacıdır. Bu ünitede karmaşık karar problemlerinin gösterimi ve çözümünde kolaylık sağlayan karar ağacı ve olasılıkların daha sağlıklı belirlenmesi amacıyla kullanılan Bayes yaklaşımı ele alınmaktadır.
Karar Vermede Karar Ağacı
Karar ağacı, karar probleminde yer alan tüm öğeleri çeşitli geometrik sembollerle temsil eden grafiksel bir tekniktir. Karar ağacı, karar problemine ilişkin tüm öğeleri ve ayrıntıları grafiksel olarak göstermenin yanı sıra ağaç üzerinde beklenen değer hesaplamaları gerçekleştirilerek aynı zamanda problemin çözümünün elde edilmesini de Sağlar.
Karar ağacı, olası her karar alternatifinin uygulanması durumunda karşılaşılabilecek kontrol edilemeyen değişken değerleri kümesi aynı olmayan karar problemleri için uygulanabildiği gibi, söz konusu değerler kümesinin aynı olduğu fakat her strateji için kontrol edilemeyen değişkenlerle karşılaşma olasılıklarının farklı olduğu durumlarda da kullanılır. Karmaşık karar problemlerinde karar ağacının kullanılması problemi daha küçük parçalara ayırarak diğer bir ifadeyle basite indirgeyerek çözme olanağı sağlar. Strateji tablosu ve ilgili karar ölçütleri yardımıyla çözülebilecek karar problemleri için de kullanılabilen karar ağacı tekniği özellikle birden fazla kararın ardışık olarak verilmesini gerektiren problemlerinin gösterimi ve çözümü için çok kullanışlıdır.
Karar ağacının öğeleri, karar düğümü, şans düğümü, bitiş düğümü, dal, sonuç ve olasılık biçiminde sıralanır. Karar probleminin çözüm sürecinde beklenen değerler hesaplanarak karar ağacına eklenir.
Karar ağacı üzerinde kare şekliyle gösterilen karar düğümü, karar değişkenini temsil eder. Karar verici, karar düğümünde en az iki seçenek arasından bir seçim yaparak karar verir. Karar ağacı genellikle verilen ilk kararla başlatıldığından, karar ağacının sol yanında konumlandırılan bir karar düğümü aynı zamanda başlangıç düğümü olur. Başlangıç düğümü kök düğüm olarak da ifade edilmektedir.
Karar ağacı üzerinde daire şekliyle gösterilen şans düğümü, rassal değişkeni (şans değişkeni) temsil eder. Şans düğümü en azından iki olası sonucu gösterir. Karar ağacında belirli olasılıklarla belirli değerleri alabilen olayları simgeler. Açıklamalardan da anlaşılabileceği gibi şans düğümü doğal durumlara karşılık gelir. Bitiş Düğümü, karar ağacında kısa düşey çizgi ile gösterilir. Bitiş noktasını yarış düğümü olarak kabul eden dal için nihai sonucu belirtir. Problemin karar veya maliyet yapılı olmasına göre bu nokta üzerinde toplam kar veya maliyet gösterilir. Karar ya da şans dalından sonra bir bitiş düğümü varsa, bitiş düğümüne bağlanan dal, aynı zamanda bir bitiş dalı olur. Karar vericinin bu noktaya ulaşırken izlediği yol ise senaryo olarak adlandırılır.
Karar ağacı üzerinde düğümleri birbirine bağlayan çizgilere dal adi verilir. Bir karar düğümünün sağından çıkan çizgiye karar dalı denirken, bir şans düğümünün sağından çıkan çizgi şans dalı olarak adlandırılır. Yukarıdan aşağıya doğru çizilebilen karar ağaçları da olabilmesine rağmen, karar ağaçlarının çiziminde genel yaklaşım olarak soldan sağa doğru bir yön izlenir. Bir şans düğümünden birden fazla dal çıkar. Her bir şans dalının belirli bir ortaya çıkma olasılığı bulunmaktadır. Standart karar ağacı yaklaşımında şans dalları üzerinde yer verilen ondalıklı sayılar bu olasılıkları ifade eder. Bir şans düğümünün tüm çıktılarına ilişkin olasılıkların toplamı 1 olmalıdır.
Sonuç, bitiş düğümünde ortaya çıkan parasal tutardır. Net kâr ya da yatırımın geri dönüşü olarak da adlandırılabilen sonuç toplam gelirle maliyetler arasındaki farktır. Sonuç pozitif veya negatif olabilir. Pozitif sonuç net kâra, negatif sonuç net maliyete eşdeğerdir.
Karar Ağacı oluşturulurken yatay doğrultuda soldan sağa doğru bir yön izlenir. İlk düğüm genellikle bir karar düğümüdür. Karar düğümü ağaca yerleştirildikten sonra bu düğüme ilişkin karar değişkeninin alabileceği tüm olası değerler, düğümden sağ tarafa çıkan dallar (karar dalları) biçiminde çizime eklenir. Daha sonra, başlangıç kararından sonra ortaya çıkması beklenen olaylar veya kararlarla ilişkili bir şans düğümü veya bir diğer karar düğümü eklenir. Bir şans düğümünün sağ tarafında yer alan şans dallarına, doğal durumları kendilerine ait olasılıklarla birlikte eklenir. Ağacın çizimi bu şekilde soldan sağa doğru, sonuçlara ulaşılan bitiş düğümlerine kadar sürdürülür. Başlangıç düğümünden bitiş düğümüne giden bir yol izlendiğinde elde edilecek kazanç ya da yapılacak ödeme sonuç olarak dalın bitiş noktasına yazılır. Böylece Karar Ağacı, problemin tüm bileşenlerini tek bir grafik üzerinde gösterir.
Bir karar probleminin karar ağacı ile çözümü için geriye doğru sonuç çıkarma veya geriye doğru katlama adı verilen analiz yöntemi kullanılır. Bu analiz yönteminin varsayımı, başlangıç seçeneğinin değerlendirilmesi için ilgili seçeneğin seçilmesi sonrasındaki tüm karar ve şans değişkenlerinin de dikkate alınması gerektiğidir. Bu nedenle ağacın en sonunda yer alan karar ve şans düğümleri ilk adımda analiz edilir ve sonra sırasıyla bir önceki noktalar incelenir ve bu işlemler başlangıç düğümüne ulaşılıncaya değin sürdürülür. Karar ağacı oluşturulurken soldan sağa doğru bir akış izlenmekte iken çözüm sürecinde ise işlemler tersine, sağdan sola doğru yürütülmektedir.
Bir şans düğümünden çıkan tüm doğal durumların beklenen değerleri (sonuç x olasılık) hesaplanır ve tümü toplanarak ilgili şans düğümüne ilişkin beklenen değer yazılır. Şans düğümü hesaplamasındaki beklenen değer, ilişkili karar seçeneklerinin göreli faydalarını ölçmenin bir yoludur. Bir karar düğümünde her bir karar seçeneği için hesaplanan faydalar karşılaştırılır ve aralarında en iyisini (amaca en uygununu, maks veya min) seçip diğerleri göz ardı edilir. Seçilen karar seçenekleri dal üzerine çizilen çift çizgiyle (//) işaretlenir.
Karar ağaçlarının oluşturulması ve karar ağaçları üzerindeki hesaplamalarla ilgili grafiklerin de yer aldığı örnekler için kitabınızdaki Örnek 4.1 (s.54) ve Örnek 4.2 (SF59) incelemeniz yararınıza olacaktır.
Karar Vermede Bayes Teoremi
Bayes teorimi, karar vericinin parametreler hakkında yapacağı tahminlerde sahip olduğu önsel bilgilerini (önceden edinilmiş sübjektif veya objektif bilgilerin) sonradan yapılan araştırmalar sonucunda elde edeceği ek bilgileri ilişkilendirilmesinde kullanılır. Bayes teoreminin bir karar probleminin çözümünde kullanılmasında iki aşama söz konusudur. Öncelikle önsel bilgiye göre tahmin edilmek istenen parametrelere ilişkin bir başlangıç olasılık dağılımı belirlenir. İkinci aşamada ise, örnekten elde edilen (araştırmalar sonucu) ek bilgilere göre parametrelerin bilgi sonrası dağılımı belirlenir. Elde edilen değer maksimum veya minimum değerin seçileceği karar sürecinde kullanılır.
Kitabınızda Bayes teoremi ile ilgili formülsel açıklama ve örnek yer almaktadır. Fakat burada bir örnekle özetleyebilir. Örneğin, bir ürün A ve B makinesinde üretiliyor olsun. Üretilen ürünlerin %25’i A, %75’i B makinesinde üretilmekte diyelim. Bu makinelerden A, %10 olasılıkla ürünü bozuk üretiyor. B ise %20 olasılıkla ürünü bozuk üretiyor. Şimdi, üretilen ürünlerden rasgele elimize bir ürün aldığımızda, Bu ürünün A makinasının ürettiği bozuk bir ürün olma ihtimali nedir? Hesaplamaları şöyle:
Üretimde; A’dan bozuk ürün gelme olasılığı=0.25 x 0.10 = 0.025
B’den bozuk ürün gelme olasılığı= 0.75 x 0.20 = 0.15
Toplam bozuk ürün gelme olasılığı =17.5
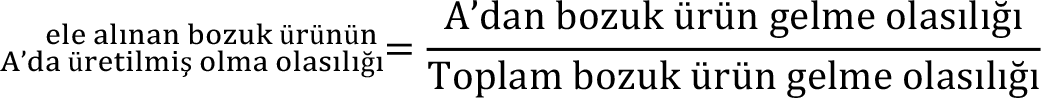
Bu olasılık 0.025/0.175 = %14.29’dur.
Bayes teoreminde Ai=(i=1,2,3,….,n) karşılıklı ayrık ve bütüne tamamlayan olaylar olmak üzere; B olayının gerçekleştiği bilindiğine göre Ai olayının gerçekleşme olasılığı aşağıdaki formülle hesaplanır:
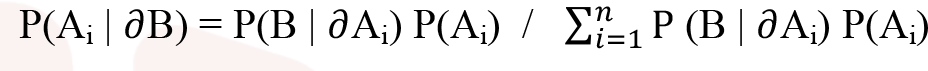
Bu formülde;
P(Ai | B) : B olayının meydana geldiği bilindiğinde Ai’nin ortaya çıkma (koşullu) olasılığını, diğer bir ifade ile olabilirliklerini
P(Ai) : Ai olayının önsel (başlangıç) olasılığı P(B|Ai) : Ai olayının meydana geldiği bilindiğinde B’nin ortaya çıkma (koşullu) olasılığını, diğer bir ifade ile olabilirliklerini.
-
2025-2026 Bahar Dönemi Ara (Vize) Sınavı İçin Sınav Merkezi Tercihi
date_range 11 Şubat 2026 Çarşamba comment 3 visibility 655
-
AÖF 2025-2026 Öğretim Yılı Bahar Dönemi Kayıt Yenileme Duyurusu
date_range 1 Şubat 2026 Pazar comment 3 visibility 388
-
2025-2026 Öğretim Yılı Güz Dönemi Ara (Vize) Sınavı Sonuçları Açıklandı!
date_range 16 Aralık 2025 Salı comment 5 visibility 896
-
2025-2026 Güz Dönemi Dönem Sonu (Final) Sınavı İçin Sınav Merkezi Tercihi
date_range 3 Aralık 2025 Çarşamba comment 3 visibility 886
-
2025-2026 Güz Dönemi Ara (Vize) Sınavı Sınav Bilgilendirmesi
date_range 2 Aralık 2025 Salı comment 2 visibility 732
-
Başarı notu nedir, nasıl hesaplanıyor? Görüntüleme : 26814
-
Bütünleme sınavı neden yapılmamaktadır? Görüntüleme : 15428
-
Harf notlarının anlamları nedir? Görüntüleme : 13621
-
Akademik durum neyi ifade ediyor? Görüntüleme : 13388
-
Akademik yetersizlik uyarısı ne anlama gelmektedir? Görüntüleme : 11171