Tıbbi İstatistik Dersi 5. Ünite Özet

Olasılığa Giriş

İstatistik biliminin temelini oluşturan olasılık, belirsizlik durumunda karar almayı sağlar. Rassallığı içeren olasılık, herhangi bir olayın meydana gelme şansıyla ilgilenir. Genel olarak olasılık, meydana gelmesi arzu edilen olay sayısının, olayın nihai tüm sonuçlarının sayısına olan oranı olarak tanımlanır.

Belirsizliğin bir ölçüsü olarak tanımlanan olasılık, aslında bize tesadüfi deneyin çok defa tekrarlanması durumunda bu sonuçlarla hangi şansla karşılaşabileceğimizi tümdengelim yöntemiyle anlatır. Olasılık kavramını açıklayabilmek için üç temel kavramın tanımlanmasına ihtiyaç vardır. Bunlar tesadüfi deney, örneklem uzayı ve olaydır.

Deney, Örneklem Uzayı ve Olay

Deney, varsayımsal olarak belirli koşullar altında sonsuz defa tekrarlanabilen ve her denemede hangi sonucun gerçekleşeceği konusunda belirsizliğin bulunduğu en az iki sonuçtan oluşan bir süreçtir. Tesadüfi deneye örnek olarak, bir zarın veya bir paranın atılmasını örnek verebiliriz. Bir tesadüfi deneyin tüm olası sonuçlarını içeren kümeye örneklem uzayı denir ve S harfi ile gösterilir. Deney sonuçlarından her birine ise olay denir. Olay örneklem uzayındaki temel sonuçların bir alt kümesidir.

Bir deneyin tüm olası sonuçlarının oluşturduğu S kümesinin, örneklem uzayı olarak tanımlandığını belirtmiştik. S’nin her bir elemanına örnek nokta veya örnek denir. S’nin herhangi bir alt kümesine veya örnek sonuçlardan bazılarının kümesi olaydır. Olay A ile gösterilirse A ? S 'dir. Ø olayına olanaksız olay, S olayı da kesin olay denir. Bir kesin olayın meydana gelme olasılığının sayısal değeri 1’ dir.

Permütasyon ve Kombinasyon

Tesadüfi bir deneyin sonuçlarına ilişkin olasılık hesabı yapılırken elverişli sonuçların sayısı ve olası tüm sonuçların sayısının bilinmesi için permütasyon ve kombinasyondan yararlanılır. Permütasyon n sayıda elemandan oluşan bir kümenin herhangi bir alt kümesinde yapılan farklı sıralamadır. Permütasyon ile n elemanın r li olarak n ? r koşuluyla kaç farklı şekilde sıralanabileceği elde edilebilir ve 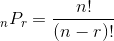ile gösterilir.

Kombinasyon ise n tane elaman arasından r tanesinin farklı şekilde seçilebileceğini vermektedir. n’ in r’li kombinasyonu n ? r koşuluyla 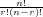formülü ile hesaplanır.

Olasılık Hesaplama

Bir olayın gerçekleşmesi için yapılan tesadüfi bir deneyde birbirinden farklı ve aynı anda olmayan N tane sonuç içinde bir olayın meydana gelme olasılığı P ile gösterilir ve bu bir olayın meydana gelme şansı olarak tanımlanır.

İki olay aynı anda meydana gelmiyorsa bu olaylara ayrık olaylar denir.

Koşullu Olasılık

İki bağımlı olaydan birincisinin gerçekleştiği bilindiğinde ikincisinin ona bağlı olarak gerçekleşme olasılığına koşullu olasılık denir. Bir olayın gerçekleşme şansı başka bir olayın gerçekleşmesine bağlı olduğunda koşullu olasılık kullanılmaktadır. A ve B olayları herhangi iki olay olsun. A olayının gerçekleştiği bilindiğinde, B olayının ortaya çıkma olasılığı koşullu olasılık olarak tanımlanır ve 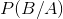ile gösterilir. Koşullu olasılık A ve B olayları için aşağıdaki gibidir (Örnek 5.8’i inceleyin).

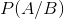: B olayı biliniyorken A olayının ortaya çıkma olasılığı,

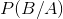: A olayı biliniyorken B olayının ortaya çıkma olasılığı,

P(A?B): A ve B olayının aynı anda ortaya çıkma olasılığıyken,

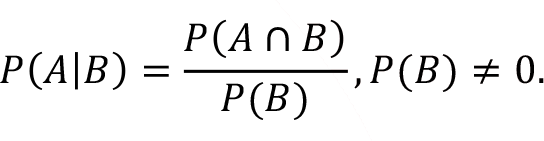
Ayrık ve Bağımsız Olaylar

İki ya da daha fazla olay bir arada meydana gelemiyorsa bu olaylara ayrık olaylar denir. Bu bir olayın otomatik olarak diğer olayın meydana gelmesini engellemek anlamına gelir. Ayrık olaylar için A veya B’nin olasılığı P(A?B) = P(A)+ P(B), ayrık olmayan olaylar için ise A veya B’nin olasılığı P(A?B) = P(A) + P(B) - P(A ? B)ile hesaplanır.

Tesadüfi Değişkenler

Tesadüfi değişken, S örnek uzayındaki her bir tesadüfi olaya sayısal değerler atayan bir fonksiyondur. Bu fonksiyon aracılığıyla örnek uzayındaki her bir sonuç reel eksende bir değere taşınır. Kısaca tesadüfi değişken, S örneklem uzayının her bir olayını yalnız bir gerçek değere dönüştürür. Bir tesadüfi değişken yalnızca sayılabilir sayıda değerler alabiliyorsa kesiklidir. Öte yandan bir tesadüfi değişken tanımlı bir aralıktaki tüm değerleri alabiliyorsa süreklidir.

Kesikli Olasılık Fonksiyonu

X, olasılık fonksiyonu P(x) olan kesikli bir tesadüfi değişken olsun. Bu durumda kesikli olasılık fonksiyonu aşağıdaki özelliklere sahip olur (Örnek 5.11’i inceleyin):

Her X değeri için P(x) ? 0,

Tekil olasılıkların toplamı 1’dir; yani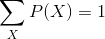

Sürekli Olasılık Fonksiyonu

X, olasılık fonksiyonu f(x) olan sürekli bir tesadüfi değişken olsun. Bu durumda sürekli olasılık fonksiyonu aşağıdaki özelliklere sahip olur.

• Her x değeri için f (x) ? 0,
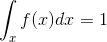• ’dir.

Sürekli bir tesadüfi değişkenin olasılık yoğunluk fonksiyonu,

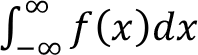şeklinde ifade edilir.

Bu fonksiyon aracılığıyla X değişkeninin a ile b arasında bir değeri alma olasılığı ise,

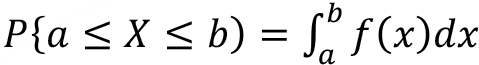ile bulunur.

Binom Dağılımı

Yapılan deneylerin sonuçları, olumlu-olumsuz, başarılıbaşarısız, iyi-kötü, ölü-sağ, pozitif-negatif gibi ortaya çıkıyorsa, bu tür deneyler sonucunda elde edilen dağılımlar Binom dağılımıdır. Tesadüfi bir deneyin başarılı ve başarısız olarak iki ayrık ve bütüne tamamlayıcı bir şekilde sonuçlanabileceği ve tek bir deneydeki başarı olasılığının p olduğunu düşünelim. Eğer birbirinden bağımsız n tane deney yapılırsa, ortaya çıkan başarı sayısı X’ in dağılımına Binom dağılımı denir. Binom dağılımı kesikli olasılık dağılımıdır. Binom dağılımı, tüm denemelerin aynı koşullarda tekrarlandığı ve her tekrarda birbirinden bağımsız iki olaydan birinin meydana geldiği deneylerde ortaya çıkmaktadır.

X, bir tek denemede başarma olasılığı p, başaramamanın olasılığı q olan n bağımsız deneme için Binom tesadüfi değişkeni ise, X’in olasılık fonksiyonu şu eşitlikteki gibidir:

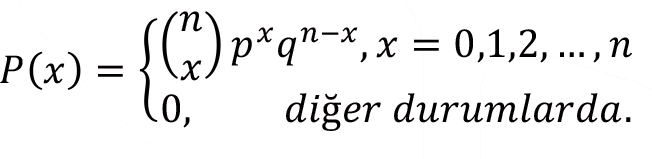
X kesikli tesadüfi değişkeni Binom dağılımına sahip ise ortalaması 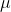= np, varyansı 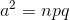, standart sapması 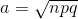ve değişim katsayısı 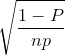" ’dir (Örnek 5.13’ü inceleyin).

Poisson Dağılımı

Binom dağılımında p olasılığının oldukça küçük olması (genellikle p<0,05) durumunda Binom dağılımı uygun bir kuramsal olasılık modeli olmamaktadır. Tesadüfi değişken belli bir zaman aralığında veya belli bir mekanda çok az yinelenen olayları göstermesi durumunda ortaya çıkan olasılık dağılımı Poisson dağılımı olarak adlandırılır.

X, 0,1,2,... olanaklı değerleri alabilen Poisson tesadüfi değişkeni olsun, X’ in olasılık fonksiyonu şu eşitlikteki gibidir:

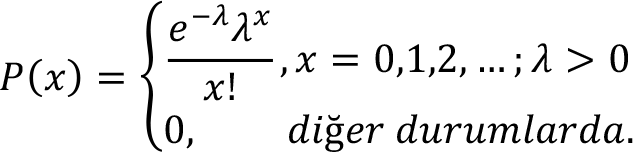
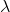, Poisson dağılımının tek parametresidir ve Poisson dağılımına sahip X değişkeninin ortalamasıdır. X kesikli tesadüfi değişkeni Poisson dağılımına sahip ise ortalaması 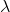, varyansı 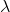ve değişim katsayısı 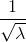’dır (Örnek 5.15’i inceleyin).

Normal Dağılım

İstatistikte en çok kullanılan ve çok geniş bir uygulama alanına sahip olan normal dağılım ya da Laplace- Gauss dağılımı ilk olarak 1733 yılında De Moivre tarafından ortaya atılmış, sonra 1809 da Gauss tarafından geliştirmiştir. Uygulamada ele alınan birçok değişken normale benzer bir dağılım gösterir. Örneğin, ölçme hataları, bebeklerin canlı doğum ağrılıkları, diastolik kan basıncı, hemoglobin düzeyi, kadınların yaşam süresi vb. gibi. Aslında, bu tür tesadüfî değişkenlerin dağılımları tam olarak bir normal dağılıma uymasa da yaklaştıkları görülür. Fakat uygulamada, çok sayıda birbirinden bağımsız olarak ortaya çıkan tesadüfî değişkenlerin bir normal dağılım gösterdikleri kabul edilir. Aritmetik ortalaması ve standart sapması farklı değerler olan çok sayıda normal dağılım düşünülebilir; herhangi bir normal dağılımın özel denklemini yazabilmek için dağılımın parametreleri

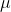ve 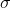olan değerlerini bilmek yeterlidir.

X sürekli tesadüfî değişkeni, gerçel sayılar uzayında tanımlanmak üzere X’in olasılık yoğunluk fonksiyonu şu eşitlikteki gibidir:

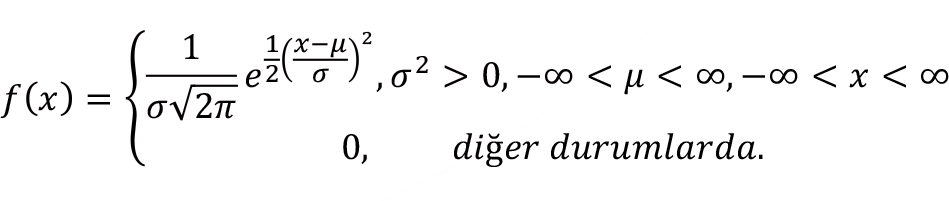
Burada; 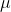normal dağılımın ortalaması, 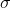normal dağılımın standart sapmasıdır (Şekil 5.1, Şekil 5.2, Şekil 5.3).

Standart Normal Dağılım

Farklı ortalama ve standart sapmalara sahip normal dağılımlar için X tesadüfi değişkenin verilen iki değer arasında olması olasılığını hesaplamak için integral almaya gerek vardır. Her olasılık değerini hesaplamak için integral almak zor olduğundan, normal dağılım özelliğine sahip bütün tesadüfi değişkenlerin yerine standart normal değişkenler geçirilerek bir tablo hazırlanmıştır. Bahsedilen standart dağılım tablosu kitabın sonunda verilmiştir.

Normal dağılım ortalama ve varyans olmak üzere iki parametresi bulunmaktadır. Farklı ortalama ve varyanslara göre çok sayıda normal dağılım eğrisi çizilebilir. Değişen ortalama ve varyanslara göre yeni olasılıkların hesabını yapmak oldukça zordur. Bundan dolayı ortalaması ve varyansı değişmeyen standart normal dağılım için olasılıklar önceden hesaplanıp, ortalama ve varyans değerlerine göre farklılaşan normal dağılımların olasılıkları bu standart dağılım aracılığıyla hesaplanabilir. Bunun için z harfi ile belirtilen standart bir değişken tanımlanır: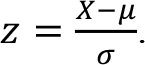

Bu z değişkeninin dağılımı, ortalaması 0 ve varyansı 1 olan normal dağılımdır ve standart normal dağılım olarak tanımlanır. Normal dağılım olasılık yoğunluk fonksiyonunda 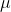= 0 ve 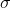= 1 yazılırsa standart normal dağılım elde edilir (Örnek 5.18’den 5.21’e kadar inceleyin).