Elektrik Makinaları Dersi 2. Ünite Özet
Elektromekanik Enerji Dönüşümü Prensipleri
Giriş
Enerjiyi bir türden diğer bir türe; dönme, öteleme veya titreşim hareketi yaparak dönüştüren cihazlara transdüser denir.
Girişindeki elektrik enerjisini mekanik enerjiye çeviren makinalara elektrik motorları, girişindeki mekanik enerjiyi elektrik enerjisine çeviren makinalara da elektrik generatörleri denir. Motor ya da generatör çalışabilmek için, hareketli parçalara ihtiyaç duyarlar.
Hareket eden hiçbir parçası olmayan, girişindeki elektrik enerjisinin türünü değiştirmeyen, buna karşılık gerilim, akım gibi bileşenlerini değiştiren makinalara transformatör adı verilir.
Enerjinin sakınımı prensibine göre enerji yoktan var edilemez veya varken yok edilemez. Sistemler enerjiyi ancak bir formdan başka bir forma dönüştürebilirler. Bir sistemde gerçekleşen enerji dönüşümleri sırasında,
- sisteme giren enerjinin bir kısmı faydalı enerjiye (örneğin işe) dönüşür,
- bir kısmı ısı enerjisine dönüşerek çevreye atılır,
- sisteme giren enerjiyle, sistemden çıkan enerji arasındaki fark, sistem içinde depo edilmiştir.
Elektromekanik enerji dönüşümü yapan, ancak işlevlerine bağlı olarak yapıları birbirinden farklı olan birçok cihaz söz konusudur;
- Transdüserler: Ölçme ve kontrol amaçlı olarak kullanılan ve genel olarak giriş ve çıkış büyüklükleri arasında doğrusal ilişki olan ve küçük işaretlerle çalışan moment motorları, mikrofon, pikap ve hoparlör gibi cihazlar.
- Röle ve elektromıknatıslar: Öteleme hareketi ile bir kuvvetin oluşturulduğu ve devrelerin açma-kapama işlemlerinde kullanılan cihazlar,
- Elektrik motor ve generatörleri: Dönme hareketi ile elektrik enerjisini mekanik enerjiye dönüştüren ya da tersini sağlayan cihazlar.
Yukarıda anılan tüm cihazlar, mekanik kısımları bir yana bırakılırsa, elektromanyetik sistemlerdir. Elektromanyetik sistemlerin elektrik ve manyetik kısımları ayrı ayrı incelenebilir.
Mekanik Büyüklükler ve Tanımlar
Elektromekanik sistemlere ilişkin davranışları açıklamakta kullanılan bazı terimler aşağıdaki gibidir.
- Konum Açısı (?): bir noktanın referans olarak seçilen sabit bir noktaya (merkeze) göre çizilen doğrultusu ile aynı merkezden çizilen referans bir doğrultu arasındaki açıdır. Bir noktanın konum açısı, referans nokta etrafında dönmesiyle değişir ve radyan [rad] ya da derece [º] ile ölçülür.
- Açısal Hız (?=d?/dt): konum açısının zamana göre değişim hızıdır ve [rad/san] cinsinden ifade edilir.
- Çizgisel Hız (v=dx/dt): bir noktanın referans olarak seçilen bir nokta ile arasındaki mesafenin zamana göre değişim hızıdır. x ötelemesi metre cinsinden ifade edildiğinde çizgisel hız (m/san) cinsinden ifade edilir. (r yarıçapı etrafında w açısal hızıyla dönen bir cismin çizgisel hızı: v = w.r)
- Açısal ivmelenme (?=d?/dt): açısal hızın zamana göre değişim hızıdır ve [rad/san2 ] cinsinden ifade edilir.
- Çizgisel ivmelenme (a=dv/dt): çizgisel hızın zamana göre değişim hızıdır ve [m/san2 ] cinsinden ifade edilir.
- Moment (dönme kuvveti): bir cisme uygulanan kuvvet ile kuvvet kolunun çarpımına eşittir. Kuvvet kolu, kuvvetin doğrultusu ile dönme ekseni arasındaki en küçük mesafedir. Moment, Newtonmetre [N.m] cinsinden ifade edilir.
Newton Kanunu: Bir cisim üzerine etki eden net bir kuvvet varsa cisim ivmelenir (hızı değişir), yoksa hızı sabit kalır. Newton kanunu, sırasıyla öteleme ve dönüş hareketleri için,
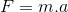
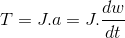
denklemleri ile tanımlanır.
İş: Bir cisim ya da sistem bir F kuvvetinin etkisi ile bir x ötelemesi yaptığında ortaya çıkan iş,
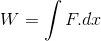 ve dönüş hareketi için,
ve dönüş hareketi için, 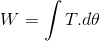 denklemleri ile tanımlanır. İşin birimi joule [J]’dir.
denklemleri ile tanımlanır. İşin birimi joule [J]’dir.
Güç: Güç, birim zamanda elde edilen iş olarak tanımlanır ve sabit kuvvet altında, sabit doğrultuda bir öteleme hareketi için,
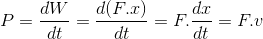
sabit moment altında dönüş hareketi için,
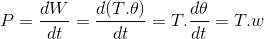
denklemleri ile ifade edilir.
Uluslararası birim sisteminde güç, watt [W] ile ölçülür (watt=joule/saniye).
Makinalarda verim, alınan iş veya gücün verilen iş veya güce oranı şeklinde tanımlanır. Elektrik generatörü verimi,
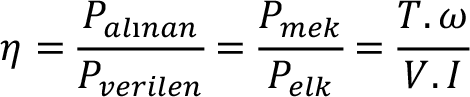
elektrik motorunun verimi,
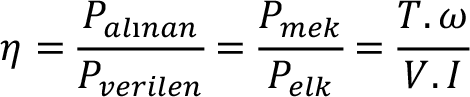
Manyetik Alan İçerisinde Akım Taşıyan İletkene Etkiyen Kuvvet
Manyetik bir alan içinden üzerinden akım geçen bir iletken üzerine bir kuvvet etki eder. Akımın büyüklüğü I, manyetik alanın genliği B, akım ile manyetik alan arasındaki açı O ve iletkenin uzunluğu l ise üzerine etki eden kuvvetin büyüklüğü,
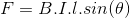 (N)
(N)
denklemiyle, yönü ise sağ el kuralı ile bulunur.
Manyetik Alan İçerisindeki Bir İletkende Endüklenen Gerilim
Faraday, bir iletkeni kesen manyetik akının büyüklüğü veya yönünde (manyetik akı kaynağının genliğindeki değişimden veya iletkenle aralarındaki hareketlerden dolayı) bir değişim olduğunda, iletken üzerinde bir gerilim endüklendiğini bulmuştur. Lenz ise endüklenen gerilimin, iletkeni kesen manyetik akıdaki değişime zıt yönde olacağını ifade etmiştir. İletkenin sabit olup, manyetik akının değiştiği durum için, Faraday ve Lenz kanunları birleştirilerek,
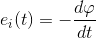
şeklinde ifade edilir. İletken N sarımlı bir bobin şeklindeyse yukarıdaki eşitlik N ile çarpılır.
Sabit manyetik akı yoğunluğu (B) içinde v çizgisel hızı ile hareket eden l uzunluğundaki bir iletkenin uçları arasında endüklenen gerilim,
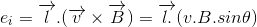
şeklinde hesaplanır ve yönü sol el kuralı ile bulunur.
Burada 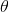 açısı,
açısı, 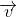 hız vektörü ile
hız vektörü ile 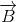 manyetik alan vektörü arasındaki açıdır.
manyetik alan vektörü arasındaki açıdır. 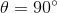 ise eşitlik
ise eşitlik
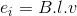
şeklinde yazılabilir. Sarım sayısı N olan bir bobin için
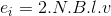
Endüklenen gerilimden dolayı iletken üzerinden geçen akımın yönü, sol el kuralıyla bulunur.
Doğru Akım (DA) Makinalarının Temelleri
Doğru Akım Makinasında Hava Aralığı Alan Dağılışı ve Endüklenen Gerilimin Şekli (Gerilimin Doğrultulması)
Doğru akım makinalarında hareketli/dönen bobin (endüvi) uçları, kollektör adı verilen bilezik dilimleri şeklinde karşılıklı levhalar üzerine irtibatlandırılır. Motor olarak çalışan elektrik makinalarında elektrik enerjisi girişi ve generatör olarak çalışan elektrik makinalarında elektrik enerjisi çıkışı bu kollektörlere (serbestçe dönmelerine müsaade edecek şekilde) temas eden fırçalar üzerinden yapılır. Kollektörler endüvi ile birlikte dönerken, fırçaların pozisyonu sabittir.
Generatör endüvi sargısının bir kolu, bir fırça altından geçerken manyetik kutuplara göre hareketinin yönü daima aynı olduğundan, o fırçadan daima aynı işaretli bir gerilim veya akım elde edilir. Dolayısıyla iki fırça arasından doğrultulmuş bir akım veya gerilim elde edilir. Akım veya gerilimin dalga şekli, endüvi ile kutup yüzeyleri arasındaki hava aralığının alan dağılımına bağlı olarak, sinüsoidal, kare dalga v.b. olabilir.
Bir tek sarım üzerinde endüklenen gerilim ( 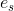 ), sarım yüzeyi ile manyetik akı arasındaki açıya bağlı olarak,
), sarım yüzeyi ile manyetik akı arasındaki açıya bağlı olarak,
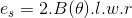
şeklinde değişir.
Bir Sarımda Endüklenen Gerilimin Ortalama Değeri
Kutup çifti sayısı p olan bir elektrik makinasında,
kutup genişliği,
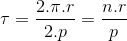
yüzey alanı,
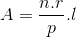
manyetik akı yoğunluğunun ortalama değeri,
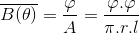
bir tek sarımda endüklenen gerilimin ortalama değeri,
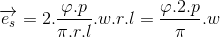 (V/sarım)
(V/sarım)
şeklinde hesaplanır.
Basit paralel sarımlı bir makinada, kutup sayısına eşit sayıda paralel kol meydana gelir. Her bir paralel kolda seri bağlı bobin sayısı, kollektör sayısı kutup sayısına bölünerek bulunabilir.
Paralel kol sayısı a, toplam sarım sayısı N olan bir jeneratör endüvisi üzerinde endüklenen gerilim,
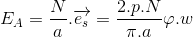
Endüvi üzerindeki toplam sarım sayısı (N) yerine toplam iletken sayısı (Z=2.N) kullanılarak,
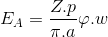
şeklinde bulunabilir.
Makinanın konstrüksiyon sabiti, açısal hızına 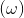 bağlı olarak,
bağlı olarak, 
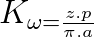 veya devir/dakika cinsinden hızına (n) bağlı olarak,
veya devir/dakika cinsinden hızına (n) bağlı olarak, 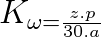 şeklinde tanımlanır.
şeklinde tanımlanır.
Bu durumda endüvide endüklenen gerilim,
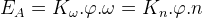
Endüvide Endüklenen Moment
Endüviden geçen toplam akım I A ise bir tek iletken üzerinden geçen akım (i i ),
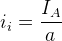
bir tek iletkene etki eden kuvvet,
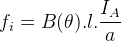
bir tek iletkene etki eden ortalama moment,
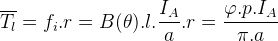
endüvi üzerine etki eden toplam moment,
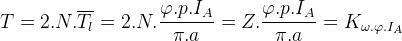
Alternatif Akım (AA) Makinalarının Temelleri
Elektrik Makinalarında Mekanik ve Elektrik Açılar
Mekanik açı: bir iletkenin bir bir elektrik makinasının sabit bir noktasına göre açısıdır.
Elektrik Açısı: bir iletkenin manyetik alana göre açısıdır
Bir iletken, bir elektril makinası içinde bir başlangıç noktasından itibaren daima aynı yönde hareket ederek tekrar başlangıç noktasına döndüğünde mekanik bir turu, bir kutup (örneğin N) hizasından hareket edip tekrar aynı işaretli kutup hizasına geldiğinde ise manyetik bir turu tamamlar. İletken mekanik bir turu tamamladığında, kutup çifti sayısı kadar manyetik turu tamamlar. Elektrik makinalarında, komşu iki kutup arası, kutup adımı olarak tanımlanır. Silindirik bir elektrik makinasında
1. Komşu iki kutup arasında elektriksel yol (açı),
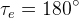
2. Komşu iki kutup arasında mekanik yol (açı)
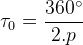
3. Mekanik çevre 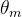 ’nin elektriksel çevre karşılığı
’nin elektriksel çevre karşılığı
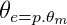
3 Fazlı Stator Sargıları
3 fazlı AA makinalarında bir faza ait bobin, birkaç bobinin seri bağlanarak statordaki oluklara dağıtılmasıyla oluşturulur. 60o e faz kuşağına sahip sargıların oluklardaki tabaka sayısına (bobin kenarı) göre iki çeşidi bulunur. Bunlar:
1.Tek tabakalı sarımlar:
a. El sarımı
b. Yarım kalıp (yarım gabari, yarım Amerikan) sarım
Çift tabakalı sarım (Tam kalıp sarım) İki bobin kenarı arasındaki açıklık bobin adımı olarak adlandırılır. Bu açıklık oluk sayısı veya elektriksel açı cinsinden verilir. Bobin adımı kutup adımına eşit olan bobinler tam adımlı bobin, bobin adımı 180o ’den küçük olan bobinler ise kesirsel adımlı bobin olarak adlandırılır.
Stator Sarım Şeması Örneği
Sarım şemasını çizebilmek için gerekli eşitlikler:
1. Bobin Adımı (Y): Bir AA makinasında oluklar çevreye eşit aralıklarla dağıtılır. Dolayısıyla kutup adımı değeri oluk sayısı cinsinden yazılırsa bu değer aynı zamanda bobin adımına karşılık gelir. Toplam oluk sayısı S olan 2p kutuplu bir makine için bobin adımı,
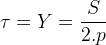
2. Bir Kutup Bölgesinde Bir Faza Ait Oluk Sayısı (Q): Bir kutup bölgesinde bir fazın kullanacağı oluk sayısıdır. “m” faz sayısını göstermek üzere,
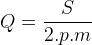
3. Oluk Açısı (Oluk Adımı, 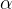 ): İki oluk arasındaki elektriksel açıdır.
): İki oluk arasındaki elektriksel açıdır.
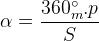
4 kutuplu, 24 oluklu, 3 fazlı bir stator için hesaplamalar:
Çizime renk sayısı kadar aynı renkte oluklar yan yana işaretlenerek başlanır. Daha sonra yarım kalıp sarım şemasında pratik yol olarak, ilk oluklardan başlayarak uzun ve kısa kenarlar işaretlenir. Uzun kenarlar bobinin birinci kenarı, kısa kenarlar ikinci kenarlarını gösterir. Çizimde karışıklığı önlemek için bobinlerin sadece yarısı çizilir (bkz. Şekil 2.22).
Daha sonra bobinlerin uzun ve kısa kenarları birleştirilerek, bobinlerin çizimi tamamlanır. Oluşturulan bobin gurubunun girişi 1. bobinin girişi, çıkışı ise, 2. bobinin çıkışıdır.
Her renkten iki gurup oluşur. Tek tabakalı sarımlarda bir fazdaki bobin gurubu sayısı çift kutup sayısına eşittir. Çift tabakalı sarımda (tam kalıp sarım) bobin gurubu sayısı kutup sayısına eşit olur.
Sonraki adım faz giriş uçlarını ve bobin guruplarının birbiri ile bağlantısını gerçekleştirmektir. Bundan sonra faz çıkış uçları da bulunmuş olur (Şekil 2.24).
Faz giriş uçları U, V, W çıkış uçları X, Y, Z harfleri ile gösterilir. Faz giriş uçları arasındaki elektriksel açı 120º olması gerektiğinden, ?=30º’dir. Dolayısıyla, 4 oluk saydıktan sonra bir sonraki faz giriş ucu bulunur. Bobin gurupları arasında ise 180º elektriksel açı bulunur.
Statorun Bir Fazında Endüklenen Gerilimin Hesabı
Bir Sarımda Endüklenen Gerilim
Şekil 2.25’teki gibi, rotor tekerleği ns senkron devir sayısı ile dönmekte olan çıkık kutuplu bir senkron makinanın rotoru üzerinde oluşturulan manyetik alan, genliği ve yönü sabit olduğundan, statordaki bir iletkende hareket yolu ile bir gerilim endüklenir. Bu ani gerilim değerinin efektif değeri,
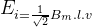 (V/iletken)
(V/iletken)
Endüklenecek gerilimlerin açısal frekansı,
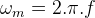 (rad/s)
(rad/s)
Bu frekansa sahip gerilimleri endüklemek için rotorun dönmesi gereken hız,
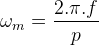 (rad/s) veya;
(rad/s) veya;
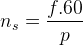 (d/d)
(d/d)
İç çapı D olan stator sargısı içinde,n s (d/d) hızıyla dönen iletkeninin rotor üzerindeki manyetik alana göre çizgisel hızı yaklaşık olarak,
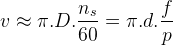 (m/s)
(m/s)
DA makinalarında olduğu gibi, hava aralığındaki ortalama akı değerini kullanmak daha uygundur. (Şekil 2.13 referans alınarak) l boyundaki 2p kutuplu D iç çaplı stator içinde ortalama akı yoğunluğu değeri,
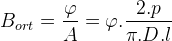
maksimum akı yoğunluğu değeri,
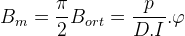
bir tek iletkende endüklenen gerilimin efektif değeri,
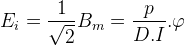
şeklinde elde edilir.
Anlık gerilim değeri, şekil katsayısı (k ş ) dikkate alınarak ve kutup başına manyetik akı 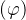 ile gösterildiğinde,
ile gösterildiğinde,
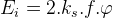
şeklinde yazılabilir. (Sinüs dalgasının şekil katsayısı 1.11’e eşittir).
Bir Bobinde Endüklenen Gerilim
Tam adımlı bobinde, bobin kenarları N ve S kutuplarının eksenine aynı anda girdiğinden, iki kenarda endüklenen gerilimler aynı fazdadır. Kesirsel adımlı bobinde ise ikinci kenar S kutbunun eksenine birinci kenara göre ߺ sonra girmektedir. Bu durumda iki kenar gerilimi arasında ß kadar faz farkı meydana gelir. Bunun sonucunda kesirsel adımlı bobinde endüklenen gerilim değeri, tam adımlı bobine göre cos(ß/2) kadar azalır. Bu azalma, bobin adım katsayısı (ka) olarak tanımlanır.
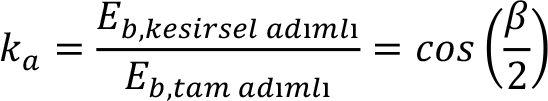
Bir bobinde endüklenen gerilim, bobin adım katsayısı ile,
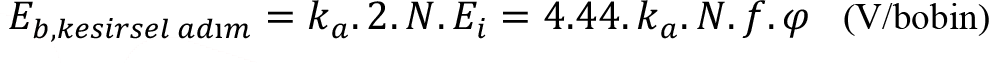
şeklinde yazılır.
Bir Bobin Gurubunda Endüklenen Gerilim
Bobin gurubunun bir tek oluğa yerleştirilmesi halinde, tüm bobin kenarlarında endüklenen gerilimler aynı fazda olur ve toplam gerilim,
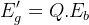
şeklinde hesaplanır.
Farklı oluklara dağıtılan bir bobin gurubunda ise sargı kenarları üzerinde endüklenen gerilimler arasında belli bir faz farkı (?) oluşur. Dolayısıyla bir bobin grubunda endüklenen gerilim her bir kenar üzerinde endüklenen gerilimler vektörel olarak toplanarak bulunur.
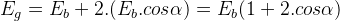
Farklı oluklara dağıtılan bir bobin grubu üzerinde endüklenen gerilimin, aynı oluğa yerleştirilmiş bobin grubunda endüklenen gerilime oranı, bobin dağıtım katsayısı (k d ) olarak tanımlanır.
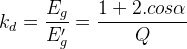
Bobin dağıtım katsayısı kullanılarak bir grupta endüklenen toplam gerilim,
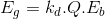 (V/grup)
(V/grup)
şeklinde ifade edilir.
Statorun Bir Fazında Endüklenen Gerilim
3 fazlı bir makinanın stator sargısında bulunan gurupların ağırlıklı olarak seri bağlı olduğu kabul edilirse, bir fazda endüklenen gerilim,
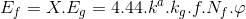
şeklinde yazılabilir. Burada N f , bir fazdaki toplam sarım sayısıdır ve
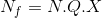
şeklinde hesaplanır.
-
2025-2026 Bahar Dönemi Ara (Vize) Sınavı İçin Sınav Merkezi Tercihi
date_range 11 Şubat 2026 Çarşamba comment 4 visibility 1373
-
AÖF 2025-2026 Öğretim Yılı Bahar Dönemi Kayıt Yenileme Duyurusu
date_range 1 Şubat 2026 Pazar comment 1 visibility 678
-
2025-2026 Öğretim Yılı Güz Dönemi Ara (Vize) Sınavı Sonuçları Açıklandı!
date_range 16 Aralık 2025 Salı comment 3 visibility 1162
-
2025-2026 Güz Dönemi Dönem Sonu (Final) Sınavı İçin Sınav Merkezi Tercihi
date_range 3 Aralık 2025 Çarşamba comment 1 visibility 1159
-
2025-2026 Güz Dönemi Ara (Vize) Sınavı Sınav Bilgilendirmesi
date_range 2 Aralık 2025 Salı comment 1 visibility 949
-
Başarı notu nedir, nasıl hesaplanıyor? Görüntüleme : 26908
-
Bütünleme sınavı neden yapılmamaktadır? Görüntüleme : 15497
-
Harf notlarının anlamları nedir? Görüntüleme : 13759
-
Akademik durum neyi ifade ediyor? Görüntüleme : 13439
-
Akademik yetersizlik uyarısı ne anlama gelmektedir? Görüntüleme : 11217