Elektrik Makinaları Dersi 1. Ünite Özet
Manyetik Malzemeler Ve Manyetik Devreler
Giriş
Elektromekanik enerji dönüşümü yapan bütün döner elektrik makinaları, motor veya jeneratör olarak çalıştırılabilirler. Motor çalışmada, makinaya verilen elektriksel enerji mekanik enerjiye; jeneratör çalışmada ise, makinaya verilen mekanik enerji elektriksel enerjiye dönüştürülür. Bu tanımlamalardan anlaşılacağı üzere bir elektrik makinası, biri mekaniksel diğeri elektriksel olmak üzere iki farklı ortamı birbirine bağlar. Makinalar için gerekli manyetik alanı oluşturduğumuz devreye manyetik devre ismini veririz. En basit temel manyetik devre , manyetik alana ait kuvvet (akı) çizgilerini taşıyan ve ferromanyetik (demir özlü veya çelik) bir malzemeden imal edilen nüve ile manyetik alan kaynağı olan sargı’dan meydana gelir.
Manyetik Malzemeler
Akım taşıyan bir iletken kendi etrafında manyetik alan meydana getirir. Ortaya çıkan bu manyetik alan iletkendeki serbest elektrik yüklerinin (elektronların) hareketi ile ortaya çıkar. Manyetik alana ait kuvvet çizgilerinin yönü sağˆ ele kuralı ile belirlenir. Sağ el kuralında I akımı taşıyan iletkeni, başparmağımız akım yönünü gösterecek şekilde sağˆ elimiz ile kavradığımızda, dört parmağımızın yönü, kuvvet çizgilerinin yönünü gösterir.
Manyetik Malzemelerin Sınıflanması: Malzemeye uygulanan H manyetik alan şiddetine karşılık malzeme içersinde manyetik akı yoğunluğu değeri elde edilir. Manyetik akı yoğunluğu aşağıdaki formül ile belirlenir.
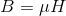 yazılan eşitlikte;
yazılan eşitlikte;
B: Manyetik akı yoğunluğu (Tesla, T)
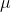 : Manyetik geçirgenlik (Henry/metre, H/m)
: Manyetik geçirgenlik (Henry/metre, H/m)
H: Manyetik alan şiddeti (Amper/metre, A/m),
Diamanyetik Malzemeler : Diamanyetik malzemeler, uygulanan kuvvetli bir manyetik alan şiddetine karşılık çok zayıf ve negatif değerlikli manyetik alınganlık değeri gösterirler. Negatif değerlikli alınganlık göstermesi, manyetik alan tarafından hafifçe itilecekleri anlamını taşır. Uygulanan alan kaldırıldıktan sonra kalıcı bir mıknatısiyet barındırmazlar. Örnek: altın, gümüş, bakır, civa, bizmut, su, tahta vb.
Paramanyetik Malzemeler: Paramanyetik malzemeler manyetik alan tarafından zayıfça çekilirler ve küçük miktarda pozitif değerli manyetik alınganlık gösteririler. Bu malzemeler sıcaklığa karşı oldukça duyarlıdırlar. Alüminyum, uranyum ve pilatinyum gibi paramanyetik mazlemelerin düşük sıcaklıklarda mıknatıslanmaları artar. Diğer paramanyetik malzemelere örnek olarak magnezyum, titanyum, tungsten, molibden ve lityum sayılabilir.
Ferromanyetik Malzemeler: İsminden anlaşılacağı üzere ağırlıklı olarak demir veya demir özlü malzemeler olarak bilinmesine karşılık, nikel ve kobalt gibi malzemeler de ferromanyetik malzemelerdir. Kendi aralarında yumuşak ve sert olarak da sınıflandırılırlar. Demir gibi yumuşak malzemeleri mıknatıslamak kolay iken, nikel ve kobalt gibi malzemeler zor mıknatıslanırlar. Ancak tersine demir kalıcı mıknatısiyetini yitirme eğiliminde iken, diğerleri mıknatısiyetlerini koruma eğilimindedirler.
Mıknatıslanma (B-H ) Karakteristikleri : Kısaca B-H karakteristiği olarak adlandırılan bu karakteristikler, kısaltılmış adından da anlaşılacağı üzere, malzemede elde edilen B manyetik akı yoğunluğu değerinin, uygulanan manyetik alan şiddeti değeri H ile değişimini verir. Malzemelerin B-H karakteristiği analizinde Amper yasası uygulanmaktadır. Amper kanununun tanımına göre , bir manyetik devreye uygulanan H manyetik alan şiddetinin, kapalı bir yol boyunca integrali, kapalı yol içinde kalan toplam akım değerine eşittir. Bir manyetik devreye uygulanan manyetik alan şiddeti devredeki toplam Ampersarım (NI) (Amper-sarım) ile doğru orantılıdır. Ampersarım değeri sargı tarafından manyetik devreye uygulanan manyetomotor kuvvet (mmk) olarak tanımlanır ve birimi (A- sarım/m) olarak da alınabilir.
Sabit Mıknatıslar: Günümüzde motor ve generatörlerde manyetik alan kaynağı olarak sabit mıknatıslar yaygın olarak kullanılmaktadır.
Manyetik Devreler
En basit manyetik devre, kapalı devre oluşturan ve ferromanyetik malzemeden imâl edilen bir nüve ile bu nüve üzerine sarılmış N sarımlı, I akımı taşıyan bir sargıdan oluşur. Mıknatıslanma karakteristiklerini anlatırken NI değerinin, manyetik devreye uygulanan mmk değeri olarak tanımlandığını görmüştük. Sargı akım taşımaya başladığı andan itibaren devreye bu mmk değerini uygular ve devreden bir ? akısı akmaya başlar. Mmk, elektrik devrelerindeki gerilim kaynağımızın emk değerine, ? akısı da akıma karşılık gelir. Bir elektrik devresinde akım nasıl bir direnç ile karşılaşıyorsa, manyetik devrelerde de ? akısı bir manyetik direnç ile karşılaşır. Bu karşılaştırmalarla, manyetik bir devrenin bir elektrik devresine benzetilmesi mümkündür.
Manyetik devrelerin bir elektrik devresine benzetilmesi bize, elektrik devrelerinde geçerli olan bütün kanun ve teoremlerin manyetik devrelere de uygulanabileceğini gösterir. Elektriksel bir büyüklüğe karşılık gelen manyetik büyüklüğü aşağıdaki tablodaki gibi gösterebiliriz.
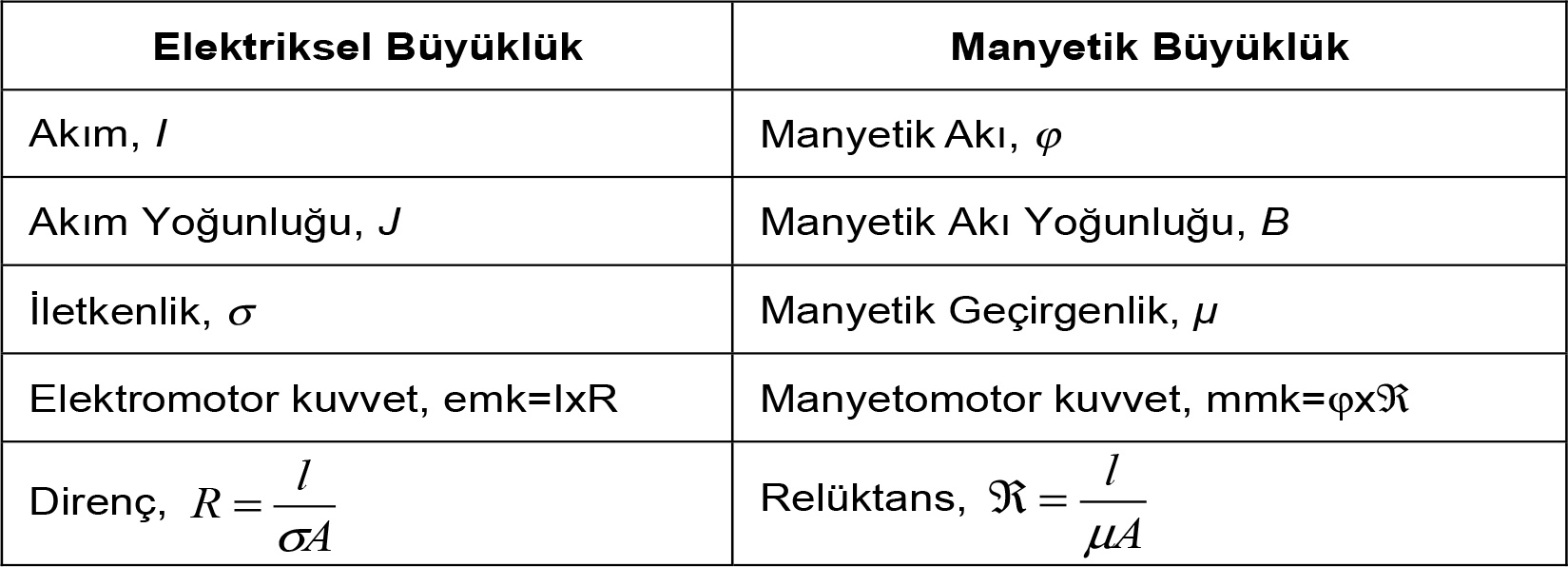
Çok Gözlü Manyetik Devreler: Bazı manyetik devrelerde birden fazla pencere ve birden fazla sargı olabilir. Bu durum çok gözlü ve birden fazla gerilim kaynağının bulunduğu bir elektrik devresine karşılık gelir. Elektrik devrelerinde çok gözlü devrelere uygulanan çözüm yöntemleri, manyetik devrelere de uygulanabilir.
Endüktörler ve Endüktans
Endüktör (bobin) manyetik alanında enerji depo eden elaman olarak tanımlanır. Elektrik alanında enerji depo eden kondansatöre karşılıktır. Solenoid ve toroid özel endüktör yapılarıdır(s:7, Şekil 1.7 ve s:22,Şekil 1.18) Solenoidin kesit alanı A, sarım sayısı N, boyu l ise, nüvenin hava olduğunu kabul ederek, solenoidde oluşan manyetik akı yoğunluğu değerini I akım değeri için aşağıdaki gibi elde ederiz.
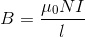
Elde edilen manyetik akı yoğunluğuna ait akı değeri, bu yapıları sarım sayısı N kere halkalayacaktır. Bu tanımla bobinler için akı halkası olarak tanımlayacağımız yeni bir kavram elde ederiz. Akı halkası değerini aşağıdaki gibi yazabiliriz.
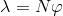
Akı halkası değerinin birimi (Wb-sarım) olur. Endüktörün endüktansı, birimi Henry (H) olmak üzere, akı halkası değerinin taşıdığı akıma oranıdır.
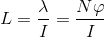
Solenoidin Endüktansı: Silindirik yapıdaki solenoidin dik kesit alanının A olduğunu kabul edelim. Solenoid için akı halkası aşağıdaki gibi yazılır.
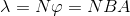
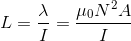
Toroidin Endüktansı
Bir toroidin endüktans değeri de aşağıdaki gibi elde edilir.
(s:7, Şekil 1.7’ye göre)
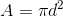
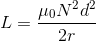
-
2025-2026 Bahar Dönemi Ara (Vize) Sınavı İçin Sınav Merkezi Tercihi
date_range 11 Şubat 2026 Çarşamba comment 4 visibility 1373
-
AÖF 2025-2026 Öğretim Yılı Bahar Dönemi Kayıt Yenileme Duyurusu
date_range 1 Şubat 2026 Pazar comment 1 visibility 678
-
2025-2026 Öğretim Yılı Güz Dönemi Ara (Vize) Sınavı Sonuçları Açıklandı!
date_range 16 Aralık 2025 Salı comment 3 visibility 1162
-
2025-2026 Güz Dönemi Dönem Sonu (Final) Sınavı İçin Sınav Merkezi Tercihi
date_range 3 Aralık 2025 Çarşamba comment 1 visibility 1159
-
2025-2026 Güz Dönemi Ara (Vize) Sınavı Sınav Bilgilendirmesi
date_range 2 Aralık 2025 Salı comment 1 visibility 949
-
Başarı notu nedir, nasıl hesaplanıyor? Görüntüleme : 26908
-
Bütünleme sınavı neden yapılmamaktadır? Görüntüleme : 15497
-
Harf notlarının anlamları nedir? Görüntüleme : 13759
-
Akademik durum neyi ifade ediyor? Görüntüleme : 13439
-
Akademik yetersizlik uyarısı ne anlama gelmektedir? Görüntüleme : 11217