Enerji Yönetimi ve Politikaları Dersi 4. Ünite Özet
Enerji Ekonomisi Projelerinde Ekonomik Analiz Yöntemleri
Giriş
Yatırım projelerinin değerlendirilmesi, ekonomik karşılaştırmayı yapabilecek farklı teorik hesaplamaların kullanılmasını içermektedir.
Projeler ve yatırım değerlendirmelerinde diğer tüm çalışmalardaki gibi çeşitli alternatiflerle karşı karşıya kalınır ve bir hedefe ulaşılmaya çalışılırken hangi yöntemin en kısa, en güvenli olduğu düşünülerek en uygun olanına karar verilir. Alternatif yollardan en ekonomik ve en yararlı olanının seçilmesi ise farklı yöntemlerin karşılaştırılması ve değişik değerlendirme kriterleri kullanılmasıyla mümkün olmaktadır.
Ekonomik Analiz Yöntemlerine İlişkin Tanım ve Kavramlar
Bileşik faiz , bir faiz döneminde faiz hesaplanırken anaparaya o döneme kadar tahakkuk eden faiz de eklenerek yapılıyorsa bu tür faiz hesaplamasına bileşik faiz hesaplanmasıdır.
Bugünkü değer , projenin çeşitli tarihlerdeki nakit akımlarının, faiz oranlarını da dikkate alarak bugünkü değere indirgenmesidir.
Ekonomik ömür , bu yatırıma ait yıllık eşdeğer masraf (YEM)’in minimum olduğu yıl olarak tanımlanmaktadır. Ekonomik ömür, yatırımın ya da varlığın, bu yatırıma ait yıllık eşdeğer net hâsıla (YENH)’nin maksimum olduğu yıl olarak tanımlanmaktadır. Ekonomik ömür aslında yatırımın ekonomik olarak işletilebildiği bir süredir ve yatırımdan beklenen ekonomik hizmet süresi olarak da değerlendirilebilir.
Gelirler , yapılan herhangi bir yatırım için, yatırımın ekonomik ömrü boyunca belirli süreler esas alınarak beklenen gelir değerleridir. Nakit akım çizelgesinde gelir değerleri pozitif(+) olarak gösterilmektedir.
Giderler , yapılan herhangi bir yatırım için yatırımın ekonomik ömrü boyunca belirli süreler içinde ortaya çıkan giderleri içerir. Nakit akım çizelgesinde giderler negatif(-) olarak gösterilir.
Hurda değeri , cihazın ekonomik ömrü sonunda tanımlandığı değeridir. Diğer bir deyimle hurda değeri; makine, bina, cihaz gibi bir varlığın ekonomik ömrü boyunca kullanıldıktan sonra piyasada satılabilecek satış fiyatıdır.
Ömür boyu maliyet , bir cihaz için servis ömrü boyunca yapılan tüm harcamaların toplamına verilen addır. Ömür boyu maliyet kavramı; cihazın yanında makine, üretim hattı, bina gibi pek çok donanım için de kullanılabilmektedir.
Oluşum maliyeti , cihaz ya da donanımın servise verilebilir hale getirilebilmesi için yapılması gereken yatırımların tamamıdır. Oluşum maliyetlerine makine giderleri, personel ve eğitim giderleri, ulaşım ve montaj giderleri ile alet maliyetleri ve destek teçhizat maliyetleri de dâhil edilmektedir.
İşletme ve bakım maliyetleri , cihazın kullanım ömrü boyunca işletim ve bakımı için harcanan giderlerin toplamıdır. İşletme ve bakım maliyetleri genel olarak yıllık bazda ele alınmaktadır.
Amortisman , bir cihazın ya da varlığın zaman içerisinde aşınma, yıpranma ya da demode olma gibi nedenlerle ortaya çıkan değer kaybıdır. Araziler için amortisman kaybından söz edilmemektedir. Amortisman fiziki amortisman ve fonksiyonel amortisman olarak iki başlıkta değerlendirilmektedir. Fiziki amortisman , yıllar boyu süren üretim sonucunda fiziki varlıkların yıpranması, eskimesi ya da tamamen yok olmasını ifade etmektedir. Fonksiyonel amortisman ise, fiziki varlığa talebin ortadan kalkması ya da modasının geçmesi sonucu kullanılamaz hale gelmesidir.
Gelecekteki değer , projenin çeşitli tarihlerdeki nakit akımlarının, faiz oranlarını da dikkate alarak gelecekteki herhangi bir noktaya götürülmesidir.
Geri ödeme süresi , bir yatırımın, yatırım maliyetini karşılaması için geçen süre olarak tanımlanmaktadır. Geri ödeme süresi, paranın zaman değerini dikkate alan ve almayan olmak üzere iki metotla yapılır.
Enflasyon , genel olarak, genel fiyat düzeyinin devamlı artması ve paranın değerinin düşmesi olarak tanımlanmaktadır.
Mikroekonomi , piyasa türlerini, piyasaların işleyiş mekanizmasını, farklı piyasa koşullarında firma dengesinin nasıl oluştuğunu incelemektedir.
Makroekonomi , ekonomi biliminin, toplam tüketim, toplam üretim, toplam tasarruf, toplam yatırım, toplam milli gelir ve istihdam gibi toplam büyüklüklerini inceler.
İlk yatırım , proje için ekipman ve malzemenin fiyatının yanı sıra bitmiş projenin tüm yardımcı giderlerini de kapsamı içine almaktadır. Taşıma, montaj, ruhsat gideri ve bazen ekipmanı işletmek için gerekli olan işletme sermayesi de bu giderler içerisindedir.
Mühendislik Projelerindeki Ekonomik Analiz Prensipleri ve Alternatiflerin Karşılaştırılması
Genel olarak bakıldığında mühendislik ekonomisi , ortaya konulan teknik ya da işletme projelerinin maliyet ve gelirlerini sistematik olarak değerlendiren bir bilim dalıdır. Mühendislik projelerinde analiz yapılırken pek çok alternatif değerlendirilmektedir. Bu değerlendirme yapılırken alternatiflerin ekonomik etkileri karşılaştırılır ve en uygun alternatif seçilir.
Enerji tasarruf projelerinde, şirket fonlarının optimum projelerde değerlendirilmesinde ya da herhangi bir yatırım da öz sermayenin mi kullanılacağı yoksa kredi olanaklarının mı değerlendirileceği bir karşılaştırma konusudur. Burada önemli olan nokta alternatif yatırım seçeneklerinin en iyi şekilde değerlendirilmesi ve bunlardan en uygununa karar verilmesidir. Başlangıçta problemin ana hatlarıyla belirlenmesi önemli bir adımdır. Bu süreçte konu ile ilgili bilgiler toplanarak sorunun sınırları ve boyutları belirlenmelidir. İkinci adımda soruna yönelik analizlerin yapılması gereklidir. Bu noktada, soruna yönelik çeşitli bilgi ve veriler değerlendirilerek soruna yönelik bir model oluşturulur. Ortaya konulan modelde veriler arası ilişkiler değerlendirilerek çeşitli alternatifler sıralanmalıdır. Ayrıntılı bir analiz yapılarak gerçekleşme imkânı olmayan ve uygun olmayan alternatifler elenir. Son aşamada alternatiflerden birisine karar verilerek seçim işlemi tamamlanmış olur.
Birden fazla yatırım seçeneğinin olması durumunda her bir yatırım seçeneği, teknik özelliklerine, ekonomik ömürlerine, nakit akışlarına göre değerlendirilerek farklı yaklaşımlar ortaya konulabilir. Yatırımlar karşılaştırılırken öncelikle yatırım maliyeti değerleri ortaya konulmalıdır. Yatırımın oluşturulması, cihazların yerleştirilmesi, montajı, eğitim giderleri, deneme süreci ve bunlarla ilgili giderler başlangıç harcamaları olarak değerlendirilir. Genel olarak yatırımın başlangıcı sıfır(0) noktası olarak alınarak bir akış diyagramı oluşturulur. Yatırım maliyeti başlangıçta tek defada olabileceği gibi yatırım belirli bir sürece yayılmış da olabilir. Bu süreç boyunca hem yatırım hem de yatırımın ödemeleri gerçekleşebilir. Bazı projelerde ise projenin ekonomik ömrü boyunca çeşitli dönemlerde ek yatırıma ihtiyaç duyulabilmektedir (s:102, Şekil 4.1).
Yatırımların en iyisinin seçilmesinde çeşitli zorluklar ortaya çıkmaktadır. Bunlardan en önemlisi yatırımla ilgili olarak ortaya çıkan bilgi eksiklikleriyle ilgili zorluklardır. Yatırıma karar verecek kişi ya da grup yatırımla ilgili pek çok ayrıntı ve parametreyi bildiğini ve karşılaştırdığını düşünse bile genelde yatırım kararları, gelecekte belli bir süreye yayılmış olduğundan pek çok belirsizliğe de sahip bulunmaktadır. Alternatiflerin seçilmesindeki diğer bir zorluk ölçülemeyen parametrelerle ilgilidir. Projeyle ilgili satın alınacak cihaz, ekipman gibi giderlerle kira, bakım onarım gibi giderlerin belirlenmesi güncel ölçülere göre belirli bir yaklaşımla yapılabilmektedir. Ancak projede çalışacak personel ile personelin kalitesi ve buna ödenecek bedelle ilgili belirsizlikler ortaya çıkabilmektedir.
Yatırımların Karşılaştırılmasında Başabaş Noktası Analizleri
Yatırımla ilgili projenin hangi üretim seviyesinde kâra geçeceği ve projenin emniyet seviyesine ilişkin analiz, başabaş noktası analizi ile gerçekleştirilir. Başabaş noktası analizi, yatırımların hangi üretim miktarında, ne kadarlık bir gider ile ne kadarlık bir gelir elde edeceklerini ortaya koyar. Bununla birlikte elde edilen gelirin ne kadarının kâr olduğunu da bu analizle ortaya çıkarılabilir.
Yatırım kararı verilecek projenin ekonomik ömrü boyunca sabit ve değişken giderleri bulunmaktadır. Sabit giderler , projenin ekonomik ömrü boyunca katlanmak zorunda olunan giderlerdir. Kira, aylık ödenen ücretler, ikramiye ve diğer sosyal ödemeler, yıllık tamir bakım masrafları, faiz giderleri, amortisman giderleri, arazi ya da bina vergileri, sigorta giderleri buna örnek olarak verilebilir. Değişken giderler ise, projenin ekonomik ömrü boyunca faaliyet hacmindeki değişikliklere göre farklılık gösterebilen giderleri ifade etmektedir. Üretimin mevsimsel ya da dönemsel olarak artışına bağlı olarak, işçilik, hammadde, yardımcı madde, işletme malzemesi, enerji gideri gibi değişken maliyetlerdir. Bu değerlendirmeye göre toplam giderler , sabit giderler ile değişken giderlerin toplamına eşit olacaktır.
Başabaş noktasının belirlenmesinde bazı varsayımlar göz önüne alınmaktadır. Başabaş noktasının belirlenmesindeki ilk varsayım; toplam giderlerin, sabit giderler ile değişken giderlerin toplamına eşit olduğu varsayımıdır (s:103, Şekil 4.2). Değişken maliyet giderleri, üretim ya da hizmete bağlı olarak aynı oranda artmakta ya da azalmaktadır. Diğer bir deyimle değişken giderlerin birim üretim başına sabit olduğu varsayılmaktadır. Projede söz konusu olan üretim ile ürünün fiyat politikalarında önemli değişiklikler bulunmamaktadır. Ülkenin genel fiyat düzeyi kararlı ve düzenli olarak gitmektedir. Projede söz konusu olan üretim sonucu ortaya çıkan satışlar ile stoklar arasında bir zaman uyumu bulunmaktadır. Projede söz konusu olan üretim sonucu ortaya çıkan ürünün birim satış fiyatı değişmemektedir.
Yatırım projelerinde başabaş noktası kârın sıfır (0) olduğu üretim hacmi olarak tanımlanmaktadır. Yatırım projelerinde başabaş noktası belirlemede kullanılan kavram ve ifadeleri BBNM miktar esasına dayalı başabaş noktasını, BBNSH satış hacmi esasına dayalı başabaş noktasını, SM sabit maliyeti, BF birim fiyatı, BDM birim değişken maliyetini göstermek üzere şu şekilde verebiliriz:
- Toplam Gelir (Satış Hasılatı) = Ürünün Birim Satış Fiyatı x Satış Miktarı
- Değişken Maliyet = Birim Değişken Maliyet x Satış Miktarı
- Toplam Gider = Sabit Maliyet + Değişken Maliyet
- Toplam Kâr = Toplam Gelir - Toplam Gider
- Gelir = Toplam Gider (Başabaş Noktası), kârın sıfır(0) olduğu nokta
- BBNM = SM/BF – BDM
- BBNSa = SM/1 - (BDM/BF)
Mühendislik Projelerinde Para Zaman İlişkileri
Projelerin değerlendirilmesinde paranın zaman içerisinde değer kaybı da dikkate alınarak karşılaştırmalar yapılır. Para işlemelerinin zaman içerisindeki değeri dikkate alınırken güncel faiz ile enflasyon değerleri ilişkilendirilmelidir.
Basit faiz hesabı: Paranın zaman içerisindeki değer değişimi için basit faiz hesaplamaları kullanılmaktadır. P miktarındaki bugünkü para değerinin, n yıl sonra ve i faiz oranı dikkate alındığında ortaya çıkacak faiz geliri şu eşitlikle hesaplanır:
I n =P.i.n
P miktarındaki bugünkü para değerinin n yıl sonra ortaya çıkacak faiz değeri ile birlikte toplam değeri Fn, paranın bugünkü değeri P ile ortaya çıkacak faiz geliri In’nin toplamına eşit olacaktır:
F n = P + I n = P + P. i. n = P(1 + i. n)
Bu eşitlikte F n , paranın zamanın herhangi bir noktasındaki değeridir. Aslında F n , bugün P miktarında olan bir paranın n yıl sonra sahip olacağı değeri ifade etmektedir. I n ise P miktarındaki bugünkü bir paranın i faiz oranı ile n yıl sonra alacağı değeri ifade etmektedir.
Bileşik faiz hesabı: Paranın zaman içerisindeki hesaplamalarında kullanılan diğer bir yöntem bileşik faiz hesabıdır. Bu hesaplama yönteminde birinci yılsonundaki faiz, anaparaya eklenerek ikinci yılın başı için yeni bir anapara oluşturulur. Daha sonra bu anapara esas alınarak ikinci yılda ortaya çıkacak faiz eklenir. Bunun sonucunda da ikinci yılsonundaki paranın değeri bulunur. Bu değer bugünkü paranın üçüncü yılbaşındaki değeridir. Bu yaklaşıma göre n’inci yılda ortaya çıkan faiz I n , n-1’inci yıldaki paranın değeri F n-1 ile i faiz oranının çarpımına eşittir:
I n -1=i.F n-1
Bu yaklaşıma göre n’inci yıldaki paranın değeri F n , n-1’inci yıldaki paranın değeri F n-1 ile son 1 yıldaki (periyottaki) ortaya çıkan faiz miktarı I n ’in toplamına eşittir:
F n =F n-1 +I n =F n-1 +i.F n-1 =F n-1 (1+i) n
Nakit akım şemaları: Nakit akım şeması paranın çeşitli zamanlarda nasıl bir akış gösterdiğini açıklamak üzere çizilmektedir. Nakit akım şemalarında para girişleri pozitif (+), para çıkışları negatif (-) çubuk olarak gösterilmektedir (s:107, Şekil 4.4).
Tek para toplamı için bugünkü değer P verildiğinde, gelecekteki değer F’nin bulunması: Tek bir para miktarının bugünkü değeri P’nin verildiği ve gelecekteki değer F’nin bulunması istendiğinde bileşik faiz kullanılarak nakit akım şeması modeli ile çözüm bulunacaktır. Bu amaçla şu eşitlikten yararlanılır (s:107, Çizelge 4.3):
F=P(1+i) n
Başlangıçtaki tek bir para toplamı olan P’nin n faiz periyodunda bir hesaba yatırıldığı öngörülmektedir. Her faiz periyodunda faiz oranı i olarak alınmaktadır. “n” periyodu sonunda gelecekte birikmiş para toplamı F olarak ortaya çıkmaktadır.
F=P(F|P i,n)
Gelecekteki değer faktörü (F|P i, n) “i faiz oranıyla n yılda, P bugünkü paranın, F gelecekteki değer faktörüdür” (s:118-122, Çizelge 4.4-4.8).
Tek para toplamı için gelecekteki değer F verildiğinde, bugünkü değer P’nin bulunması: Gelecekteki bir değerin bugünkü karşılığı için şu eşitlikten yararlanılır:
P=F(1+i) -n
Bulunan bu ifadeyle, gelecekteki bir tek para toplamının verilen bir i faiz oranı ve n yıl esas alınarak bugünkü değeri hesaplanacaktır. Bu eşitlikte geçen (1+i) -n için farklı faiz oranları ve farklı yıl değerleri dikkate alınarak hazırlanmış çizelgelerden yararlanılarak da çözüme ulaşılabilinir. Bu çizelgelerde (1+i) -n karşılığı olarak, gelecekteki paranın bugünkü değer faktörü (P|F i,n) değerleri oluşturulmuştur.
P=F(P|F i,n)
Para akış serileri: Tek bir para toplamı yerine yıllara bağlı olarak değişen para giriş ya da çıkışlarının bugünkü veya gelecekteki değerlerinin hesabı için para akış serileri kullanılır. Para akış serilerindeki eşitliklerde, t ile zaman değeri, A ile t zaman periyodu sonundaki para giriş ya da çıkış değerleri, i ile faiz oranı, n ile de yıl değeri gösterilmektedir. Farklı yıl ve büyüklükteki para akış diyagramı aynı zaman periyodu olarak gösterilen çubuk üzerinde bulunmaktadır (s:109, Şekil 4.5).
Para akış serilerinde A değerleri verildiğinde bugünkü değer P’nin bulunması: Para akış serilerindeki değerlerin bugünkü değerinin hesaplanmasında seri içerisindeki her bir para akış değeri bugünkü değere indirgenir, bunların toplamı para akış serisinde A değerlerinin bugünkü değerine karşılık gelecektir. Bunu hesaplayabilmek üzere aşağıdaki matematiksel ifade kullanılmaktadır:
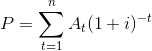
Bu eşitlikte (1+i) -t çizelgelerde (P|F i,t) faktörü haline getirilmiştir. Bu durumda (P|F i,t) ifadesi, i faiz oranıyla, t periyodundaki, gelecekteki para F’nin, P bugünkü değer faktörü olmak şu eşitlikten yararlanılabilir:
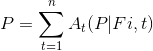
Para akış serilerinde A değerleri verildiğinde gelecekteki değer F’nin bulunması: Para akış serilerindeki değerlerin gelecekteki değerinin hesaplanmasında seri içerisindeki her bir para akış değeri gelecekte belirlenen bir zamana ötelenmektedir, bunların toplamı para akış serisinde A değerlerinin gelecekteki değerine karşılık gelecektir. Bunu hesaplayabilmek üzere aşağıdaki matematiksel ifade kullanılmaktadır:
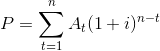
Uniform para akış serileri: Uniform para akış serilerinde seri içerisindeki tüm nakit akımları eşittir (s:111, Şekil 4.6).
Uniform para akış serilerinde A değerleri verildiğinde bugünkü değer P’nin bulunması: Uniform para akış serilerinde, A seri içerisindeki her bir para akış değeri verildiğinde, serinin bugünkü değer karşılığı P, aşağıdaki ifadelerle bulunmaktadır:
![P=A\left [ \frac{(1+i)^{n}-1}{i(1+i)^{n}} \right ]\; veya \; P=A(P|A\; i,n)](https://aofsoru.com/Content/uploads/ozet/5039c948d832-42c8-4eb9-8842-ddfe721db7ee.gif)
Yukarıdaki eşitliklerden sol taraftaki ile çözümün hesaplanması uzun zaman alabilmektedir. Diğer taraftan sağ taraftaki eşitlik ve geliştirilmiş çizelgeler yardımıyla çözüme kısa sürede ulaşmak mümkün olmaktadır.
Uniform para akış serilerinde A değerleri verildiğinde gelecekteki değer F’nin bulunması: Uniform para akış serilerinde, A seri içerisindeki her bir para akış değeri verildiğinde, serinin gelecekteki değer karşılığı F şu şekilde bulunabilir:
![F=A\left [ \frac{(1+i)^{n}-1}{i} \right ]\; veya \; F=A(F|A\; i,n)](https://aofsoru.com/Content/uploads/ozet/503957d92894-e23d-4ad5-9718-f20d4841590f.gif)
Uniform para akış serilerinde bugünkü değer P verildiğinde, A’nın bulunması: Uniform para akış serilerinde bugünkü değer P verildiğinde, seri içerisindeki her bir para akışının değeri A aşağıdaki ifadeyle bulunabilecektir:
A=P(A|P i,n)
Uniform para akış serilerinde gelecekteki değer F verildiğinde, A’nın bulunması: Uniform para akış serilerinde gelecekteki değer F verildiğinde, seri içerisindeki her bir para akışının değeri A aşağıdaki ifadeyle bulunabilecektir.
A=F(A|F i,n)
Gradiyant para akış serileri: Gradiyant para akış serilerinde verilen para akış değeri, uniform para akış serilerinde olduğu gibi sabit gitmeyip, bir önceki para akışından sabit bir miktar (G) kadar fazla olacak şekilde devam eder (s:112, Şekil 4.7).
Gradiyant para akış serilerinde G verildiğinde P bugünkü değerin bulunması: Gradiyant para akış serilerinde G artış miktarı verilmesi durumunda bugünkü değer P aşağıdaki ifade yardımıyla bulunur.
P=G(P|G i,n)
Gradiyant para akış serilerinde G verildiğinde A’nın bulunması: Gradiyant seri uniform seriye dönüştürülerek iki uniform serinin toplamı yapılır (s:114, Şekil 4.8). Gradiyant seriye eşdeğer bir seri oluşturmak için aşağıdaki ifade kullanılmaktadır:
A=G(A|G i,n)
Geometrik para akış serileri: Geometrik para akış serilerinde serideki artış ya da azalış, sabit bir yüzde değer ile gerçekleşmektedir (s:115, Şekil 4.9)
Yatırım Projelerinin Değerlendirilmesi
Yatırım projelerinin değerlendirilmesi için çeşitli ölçütler kullanılmaktadır.
Kârlılık oranı (KO) , yatırım projelerinin değerlendirilmesinde kullanılan bir yöntem olup yatırım sonucunda ne düzeyde bir kar elde edilebileceğini ortaya koymaktadır.
KO = Yıllık Net Kâr/İlk Yatırım Tutarı
Geri ödeme süresi (GÖS) , ilk yatırım tutarının ne kadarlık bir süre içerisinde geri ödenebileceğinin görüldüğü bir yöntemdir. İlk yatırım bedeli yazılırken hurda değeri çıkarılarak yazılmalıdır. Yıllık ortalama net kar bedeline de yıllık amortisman payları eklenmelidir. Bu yöntemde yıl olarak bulunan geri ödeme süresi ne kadar az ise yatırım o kadar uygun ve cazip olarak değerlendirilmektedir
GÖS = İlk Yatırım Tutarı/Yıllık Ortalama Net Kâr
Net bugünkü değer (NBD) , bir yatırım projesinin ömrü boyunca tüm yıllık sermaye giderlerinin ve tasarruflarının bugünkü değerini hesaplamaya dayanan bir yöntemdir. Hesaplama sonucunda bulunan NBD değerinin sıfır (0)’dan dan büyük olması gerekir. NBD değeri negatif (-) çıktığında proje reddedilir.
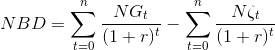
Bu ifadede NG t ,t’inci yıldaki net nakit girişini, n, projenin yaşam ömrünü, r, iskonto oranını, NÇ t ,t’inci yıldaki net nakit çıkışını göstermektedir.
Net bugünkü değer oranı (NBDO) , yatırımın faydalı ömrü boyunca nakit girişlerinin bugünkü değerinin, yatırım harcamalarının bugünkü değerine oranıdır. NBDO, fayda masraf oranı olarak da tanımlanmaktadır.
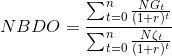
İç kârlılık oranı (İKO) , net bugünkü değeri sıfır (0) yapan iskonto oranıdır. Bu eşitlikte r, iskonto oranı deneme yanılma yöntemi ile bulunur. Diğer bir ifadeyle İKO ile NBD’yi sıfır (0) yapan iskonto değeri bulunmaya çalışılmaktadır. Bu amaçla başlangıçta tahmin edilen bir r, iskonto değeri eşitlikte yerine koyularak sonuca bakılır. Daha sonra deneme yanılma metoduyla NBD’yi sıfır (0) yapan r değeri bulunur.
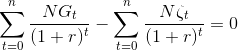
-
2025-2026 Bahar Dönemi Ara (Vize) Sınavı İçin Sınav Merkezi Tercihi
date_range 11 Şubat 2026 Çarşamba comment 4 visibility 1320
-
AÖF 2025-2026 Öğretim Yılı Bahar Dönemi Kayıt Yenileme Duyurusu
date_range 1 Şubat 2026 Pazar comment 1 visibility 660
-
2025-2026 Öğretim Yılı Güz Dönemi Ara (Vize) Sınavı Sonuçları Açıklandı!
date_range 16 Aralık 2025 Salı comment 3 visibility 1141
-
2025-2026 Güz Dönemi Dönem Sonu (Final) Sınavı İçin Sınav Merkezi Tercihi
date_range 3 Aralık 2025 Çarşamba comment 1 visibility 1137
-
2025-2026 Güz Dönemi Ara (Vize) Sınavı Sınav Bilgilendirmesi
date_range 2 Aralık 2025 Salı comment 1 visibility 939
-
Başarı notu nedir, nasıl hesaplanıyor? Görüntüleme : 26903
-
Bütünleme sınavı neden yapılmamaktadır? Görüntüleme : 15493
-
Harf notlarının anlamları nedir? Görüntüleme : 13747
-
Akademik durum neyi ifade ediyor? Görüntüleme : 13433
-
Akademik yetersizlik uyarısı ne anlama gelmektedir? Görüntüleme : 11216