Atölye Çalışması 2 Dersi 5. Ünite Özet

Giriş

Enerji günümüz dünyasında vazgeçilmez bir kavramdır ve kısaca iş yapabilme yeteneği olarak tanımlanabilir. Enerjinin birçok çeşidi vardır. Bunlar arasında potansiyel, kinetik ve kimyasal enerjiyi, elektrik enerjisini ve ısı enerjisini sayabiliriz. Enerjiden bahsederken üzerinde durulması gereken en önemli kavram “enerjinin korunumu” dur. Enerjiyi yoktan var edemeyiz ya da var olan bir enerjiyi yok edemeyiz. Ancak, enerjiyi bir türden başka bir türe dönüştürebiliriz. Örneğin; bir salıncakta sallanan çocuğu düşünelim. Dışarıdan bir etki olmadığı sürece, salıncağın salınım hareketi bir süre sonra sona erecektir. Peki, bu durumda enerji neye harcanmıştır? Tabi ki bu sorunun cevabı “sürtünme” olacaktır. Kinetik veya potansiyel enerji sürtünme yolu ile ısıya dönüşebilir. Sonuçta bir sisteme karşı yapılan iş, ya o sistemin mekanik enerjisini arttırır ya da sıcaklığını yükseltir, yani ısı enerjisine dönüşür. Yapılan mekanik iş ile sürtünme sonucu oluşan ısı miktarı arasındaki oran “ısının mekanik eşdeğeri” olarak adlandırılır.

Teorik Bilgi

Kuvvet Kavramı ve Newton’un I. Hareket Yasası

Kuvvet, bir cismin durumunda değişiklik yaratan etken olarak tanımlanır ve;

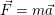
olarak verilir. SI birim sisteminde kuvvetin birimi Newton (N)’dur. 1kg kütleye 1m/s2 ivme kazandırmak için gerekli kuvvet 1 N’dur. Bir cisme birden fazla kuvvetin aynı anda uygulandığı durumlar da söz konusu olabilir. Bu durumda; cisim üzerine etki eden “net kuvvet” kavramından bahsetmek daha doğru olacaktır. Net kuvvet yerine “bileşke kuvvet” veya “dengelenmemiş kuvvet” terimleri de kullanılmaktadır. Isaac Newton, ilk olarak 1687’de “principia mathematica philosophiae naturalis (doğa bilimlerinin matematik ilkeleri)” adlı bir dergide, kütle ve kuvvet kavramlarını tanımlayan hareket kanunlarını içeren çalışmasını yayınlamıştır. Bu çalışmada belirtilen üç tane temel hareket yasası vardır. Bu bölümde bizim ilgileneceğimiz yasa Newton’un I. Hareket yasasıdır. Bu yasa eylemsizlik yasası olarak da bilinmektedir ve bir cisme etki eden net kuvvetin sıfır olması ile ilgilidir. Bu ifade, cisme etki eden birden fazla kuvvet olsa bile, bunların vektörel toplamının sıfır olduğu anlamına gelir. Newton’un I. Hareket yasasının ifadesi şu şekildedir: “Bir cisim üzerine etki eden net kuvvet sıfır olduğunda, cisim durgun ise durgun halde kalacak, hareketli ise sabit hızla hareketine devam edecektir”

Dinamometre ve Kuvvet Ölçümü

Dinamometre (kuvvet ölçer) metallerin esneklik özelliklerinden yararlanılarak yapılmış ve kuvvet ölçmekte kullanılan bir aygıttır. Dinamometrede esnek bir yay ve ölçekli bir gösterge bulunur. Uygulanan kuvvete göre yayda bir gerilme olur ve kuvvet değeri ölçek üzerinden okunur. Örneğin, dinamometrenin ucundaki çengele bir cisim takılarak cismin ağırlığı da bulunabilir. Çünkü, cisme etkiyen yerçekimi kuvveti nedeniyle dinamometredeki yayda bir gerilme olacaktır. Bu gerilme değeri cismin ağırlığına eşittir. Dinamometrede ölçülen değerler Newton (N) birimi ile verilir.

Kütle ve Ağırlık

Kütle bir cismin doğasında var olan bir özelliktir ve değişmeyen madde miktarı olarak tanımlanabilir. Kütle, eylemsizliği ölçmek için kullanılan bir terimdir ve SI birim sisteminde birimi kilogramdır. Belli bir kuvvetin etkisi altındaki küçük bir cismin büyük bir cisme göre daha çabuk hızlanacağını tahmin edebilirsiniz. Bu durum, cisimlerin kütlelerinin farklı olmasından kaynaklanmaktadır. Ağırlık terimi çoğu kez yanlış bir şekilde kütleyi ifade etmek için kullanılır. Ağırlık, yer çekiminin cisme uyguladığı kuvvettir. Kütle ve ağırlık kavramlarının tamamen farklı fiziksel özellikler olduğu unutulmamalıdır. Ağırlık bir kuvvettir, kütle ise temel büyüklüklerden bir tanesidir. Bir cismin ağırlığını ona etkiyen yerçekimi kuvveti olarak düşündüğümüzde;

FG = mg

yazabiliriz. Burada, m cismin kütlesi ve (g) ise yerçekimi ivmesidir.

İş ve Enerji

Bir cisim üzerine bir kuvveti uygulandığında cisim kuvvet yönünde yer değiştirirse, kuvvet tarafından bir iş yapılır. Yapılan işin büyüklüğü, cisme uygulanan kuvvetin büyüklüğüne, cismin yer değiştirme mesafesine ve kuvvet ile yer değiştirme arasındaki açıya bağlıdır. İş, kuvvet ile kuvvetin uygulandığı mesafenin çarpımına eşittir ve W ile temsil edilir.

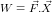
İşin birimi SI birim siteminde newton-metre (N.m)’dir. Bu birime joule (J) adı verilir. 1 joule, bir cisme 1 m boyunca etki eden 1N’luk kuvvetin yaptığı iştir.

İşin önemli bir özelliği skalar (yönü ve doğrultusu olmayan, sadece miktarı ile ifade edilebilen) bir büyüklük olmasıdır. Hem kuvvet hem de yer değiştirme yöne sahip olmalarına rağmen, bu durum iş için geçerli değildir. İş bir yöne gerek kalmadan uygun birimler ile temsil edilen bir büyüklüktür.

Bir cisim üzerine iş yapıldığında cismin hızı değişebilir veya iş yerçekimine karşı yapıldıysa cismin yüksekliği değişir. Enerji kavramı bizlere bir iş yapıldığında meydana gelen bu tip değişimleri bir bütün halinde ifade etme imkânı tanır. Bir iş yapıldığında enerjide bir değişim olur ve yapılan iş miktarı enerjideki değişime eşittir. Enerji kısaca iş yapabilme yeteneği olarak da tanımlanabilir. Enerji birçok formda karşımıza çıkabilir. Biz burada mekanik enerji ile ilgileneceğiz. Mekanik enerjinin kinetik ve potansiyel enerji olmak üzere iki çeşidi vardır. İş yaparken bir kuvvet uygularız. Örneğin bir cismi yerden kaldırdığımızda, yerçekimi kuvvetini yenmek için bir kuvvet uygularız. Bu kuvvet daha önce de belirttiğimiz gibi cismin ağırlığına eşittir. Bu durumda “yerçekimine karşı” bir iş yapmış oluruz. Burada yapılan iş (h, cismi yerden kaldırdığımız yükseklik olmak üzere);

W = Fh = mgh

şeklinde olacaktır. Olaya enerji açısından baktığımızda, yapılan iş sonucunda cisme bir potansiyel enerji kazandırmış oluruz. Bir başka örnek olarak, bir futbol oyuncusunun duran bir topa vurduğunu ve topun yerden yükselmeden hareket ettiğini düşünelim. Oyuncunun uyguladığı kuvvet sonucunda top bir hız kazanacak ve yer değiştirmiş olacaktır. Buradaki iş miktar topa hareketsel bir enerji kazandırmıştır. Bu tip bir enerji kinetik enerji olarak bilinir ve

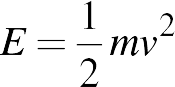
şeklinde verilir. Burada v, başlangıçta durgun olan topun uygulanan kuvvetin etkisiyle ulaştığı hızı göstermektedir. Bu durumda kuvvet tarafından yapılan iş kinetik enerjideki değişime eşit olacaktır.

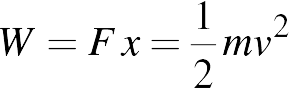
Bu örneklerden de anlaşılacağı gibi, iş enerjinin bir biçimidir. Dolayısı ile iş ve enerjinin aynı birimlere sahip olması beklenen bir durumdur. Yani enerjinin birimi de SI birim sisteminde Joule (J) olarak verilir.

Sürtünme Kuvveti ve Sürtünmeye Karşı Yapılan İş

Sürtünme kuvveti hareketi engelleyici bir özelliğe sahip olduğu için cisimlerin mekanik enerjilerinde yani hareketlerinde bir azalma olacaktır. Mekanik enerjideki bu azalma ısı enerjisine dönüşecektir. Sürtünme kuvveti ve bu kuvvetin etkidiği mesafe biliniyorsa ısıya dönüşen enerji, sürtünme kuvvetinin yaptığı işe eşit olacaktır. Sürtünme kuvvetinin yaptığı iş

Eısı = Wısı = 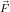_S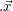

olarak verilir. Bu denklemden de görülebileceği gibi, sürtünme sonucu kaybolan mekanik enerji (yani ısıya dönüşen enerji) sürtünme kuvveti ve bu kuvvetin etkili olduğu mesafeyle doğru orantılıdır.

Sıcaklık, Isı ve İç Enerji

Isı ve sıcaklık terimleri söz konusu olduğunda, “termodinamik bilimi” karşımıza çıkar. Termodinamik kelimesi Latince “therme (ısı)” ve “dynamis (güç)” sözcüklerinden türetilmiştir. Termodinamik temel olarak ısı, sıcaklık ve iç enerji gibi kavramları barındırır ve ısı ile mekanik olaylar arasındaki ilişkiyi inceler.

Sıcaklık ölçümü için bir cisimde sıcaklıkla değişen özelliklerden yararlanılması gerekir. Bu şekilde tasarlanmış sıcaklık ölçü aletlerine “termometre” adı verilir.

Sıcaklığı düşük olan cisimler soğuk, sıcaklığı daha yüksek olanlar ise ılık ya da sıcak olarak tarif edilebilir.

Sıcaklıkları farklı iki cisim birbirlerine temas ettirildiklerinde, bir süre sonra bu iki cismin sıcaklıklarının eşit olduğu görünür. Bu durumda iki cisim ısıl dengeye ulaşmıştır. Sıcaklık bir cismin diğer cisimlerle ısıl dengede olup olmadığını belirleyen bir özellik olarak tanımlanabilir. Yani iki cisim ısıl dengede ise, sıcaklıkları aynıdır. Sıcaklık ölçülmesi için genellikle “Celsius” ölçeği kullanılır. Bu ölçeğe “santigrat” ölçeği de denir ve °C ile gösterilir. Bir başka sıcaklık ölçeği ise mutlak sıcaklık ölçeği olarak bilinen “Kelvin” dir ve K ile gösterilir. Kelvin ölçeğinde “°” simgesinin kullanılmadığına dikkat ediniz. Bu ölçekler arasındaki bağıntı

T(K) = T(°C) + 273,15

şeklindedir.

Cisimlerin birbirine teması sonucunda sıcak cisimden soğuk cisme doğru bir enerji iletimi olur. İletilen bu enerjiye “ısı” adı verilir. Isı bir enerji olduğu için, SI birim sistemindeki birimi joule (J) olacaktır. Isının tarihsel gelişimine baktığımızda yaygın olarak kullanılan bir birim de kalori (cal)’dir. Isı kalorimetre ile ölçülebilir. Isının iki cisim arasındaki enerji transferi olduğunu belirtmiştik. Dolayısıyla ısı kavramı yerine ısı akışı ya da ısı transferi terimleri de kullanılabilir. Isı akışı mikroskobik cisimlerin bir özelliği olarak görünse de, temelinde bu cisimlerin makroskobik bileşenleri yatmaktadır. Bu noktada “iç enerji” kavramı karşımıza çıkar. İç enerji termodinamikte, termodinamik bir sistemin toplam enerjisi olarak tanımlanır. İç enerji iki ana bileşenden oluşur. Bunlardan birincisi sistemdeki parçacıkların hareketine (yer değiştirme, dönme ve titreşim) bağlı olan kinetik enerji ve diğeri ise sistemin statik bileşenlerine (kimyasal bağlar gibi) bağlı olan potansiyel enerjidir. Bir sistemi ısıtarak veya sistem üzerinde iş yaparak sistemin iç enerjisi değiştirilebilir. Termodinamik yasaları, iç enerjideki artışın verilen ısı ve yapılan işin toplamına eşit olduğunu ifade eder. Bu yasa aslında enerjinin korunumu ilkesini içerir. Bir etkileşim sırasında enerji bir biçimden başka bir biçime dönüşebilir, fakat toplam miktarı sabit kalacaktır.

Isı Kapasitesi ve Öz Isı Kapasitesi

Bir maddenin sıcaklığını 1 °C arttırmak için gerekli ısı enerjisi miktarına “ısı kapasitesi” denir. Aynı miktardaki maddelerin sıcaklığını 1 °C arttırmak için gerekli enerji maddeye göre değişir. Örneğin, 1 g suyun sıcaklığını 1 °C yükseltmek için gerekli enerji 1 cal iken, 1 g’lık alüminyum kütlesi için bu enerji 0,217 cal’dir. Bir cisme Q kadar bir ısı verildiğinde, cismin ısı kapasitesine bağlı olarak sıcaklığında değişim olur ve ?T kadarlık bir sıcaklık artışı meydana gelir. Cisme verilen ısı miktarının cisimde meydana gelen sıcaklık artışına oranı “ısı kapasitesi” olarak bilinir ve “C” harfi ile temsil edilir.

C = Q/?T

Isı kapasitesinin birimleri J/K veya cal/°C olabilir. Yukarıda verilen ısı kapasitesi ifadesine göre ısı miktarı;

Q = C ?T

şeklinde olacaktır. Birim kütle başına düşen ısı kapasitesine “öz ısı kapasitesi” denir. Bu durumda bir maddenin ısı kapasitesi maddenin kütlesi ile orantılıdır. Öz ısı kapasitesi;

cöz = C/m

ile verilir. Bu ifadeye göre bir maddenin öz ısı kapasitesi, 1 g maddenin sıcaklığını 1 °C arttırmak için verilmesi gereken ısı miktarı olarak tanımlanabilir. Öz ısı kapasitesinin birimleri J/g.K veya cal/g.°C olarak karşımıza çıkabilir. Öz ısı kapasitesi maddeler için ayırt edici bir özelliktir. Alüminyum için 0,217 cal/g.°C, bakır için 0,093 cal/g.°C ve buz için 0,55 cal/g.°C’dir. 1 g maddenin sıcaklığını 1 °C arttırmak için verilmesi gereken ısı miktarı öz ısı kapasitesine bağlı olarak,

Q = m cöz ?T

şeklinde verilir.

Isının Mekanik Eşdeğeri

Mekanik bir sistemde sürtünme olduğu zaman mekanik enerjide bir kayıp olacaktır. Kaybolan bu mekanik enerji aslında ısı enerjisine dönüşmektedir. Mekanik ve ısı enerjisi arasındaki ilişki ilk olarak Thompson tarafından çalışılmıştır. James Joule bu kavramlar arasındaki ilişkileri çalışarak, enerjinin bu iki formunun eşdeğerliğini ilk defa ortaya koymuştur. Örneğin su gibi bir akışkan üzerinde bir iş yapıldığında, onun sıcaklığının arttığını görmüştür. Bunun sonucunda sistem üzerinde yapılan mekanik işin ısı enerjisine dönüştüğünü önermiştir. Joule, yaptığı deneyde kaybolan mekanik enerjinin suyun sıcaklığındaki artış ile orantılı olduğunu görmüştür. Buradaki orantı katsayısı günümüzde 4,186 J/g. °C olarak bilinmektedir. Bu değer suyun öz ısı kapasitesidir. Yani, 1 g suyun sıcaklığını 14,5 °C’den 15,5 °C’ye çıkarmak için gerekli mekanik enerji 4,186 J’dür. Daha önce yaptığımız tanımları kullanarak kalori ile Joule arasında

1 cal ? 4,186J

denkliğini yazabiliriz. Isının tarihsel gelişimi ısı enerjisi biriminin mekaniksel birim olan joule yerine daha çok kalori olarak kullanılmasına neden olmuştur. Her iki enerji farklı birimde düşünüldüğünde aralarındaki eşdeğerliği göstermek zorlaşır. Bu bölümde yapacağımız deneyde yapılan işin tamamen ısı enerjisine dönüştüğünü düşünerek, ısı enerjisinin birimini mekanik enerji birimi cinsinden ifade edeceğiz. Enerjinin korunumu prensibini ve;

W = JQ

ifadesini kullanarak “ısının mekanik eşdeğeri” olarak bilinen J katsayısını hesaplayacağız. Burada, W yapılan mekanik işi ve Q ısı miktarını temsil etmektedir. Yapılan mekanik işin tamamen ısı enerjisine dönüştüğü düşünüldüğünde, J = 1 olarak bulunmalıdır.

Isıl Çift

Isıl çift, sıcaklık ölçmekte yaygın olarak kullanılan bir aygıttır. 1822 yılında Thomas Seebeck tarafından geliştirilmiştir. Seebeck, bir iletkenin uçları arasında sıcaklık farkı olduğunda, bir potansiyel fark oluşacağını göstermiştir. Bu “termoelektrik etki” ya da “Seebeck etkisi” olarak bilinir. Eğer iletkenin iki ucu da aynı sıcaklıkta ise, bir potansiyel fark oluşmaz. Isıl çift birer uçları bir araya getirilmiş farklı iki metal veya metal alaşımlarından oluşur. Metallerin birleşme noktası sıcak nokta, diğer iki açık uç ise referans noktası olarak bilinir. Sıcak nokta ile referans nokta arasındaki sıcaklık farkı sonucu mV mertebesinde bir potansiyel fark üretilir. Üretilen potansiyel fark bir voltmetre yardımıyla okunur ve uygun tablolar kullanılarak sıcaklık değerine dönüştürülür. Ya da ısıl çift cihazı direkt olarak sıcaklığı gösterecek şekilde dizayn edilebilir. Bu durumda dijital bir sıcaklık göstergesi kullanılmalıdır. Isıl çift devresi aynı cins metallerden yapıldığında, bir potansiyel fark oluşmayacaktır. Isıl çift geniş bir aralıkta sıcaklık ölçebilir. Isıl çiftte iki farklı metal olmasına rağmen, bu halleri ile kullanılmazlar. Metallerin zarar görmesini önlemek amacıyla özel koruyucu kılıflar içerisinde kullanılırlar. Farklı sıcaklık aralıklarında çalışacak şekilde farklı ısıl çiftler yapılabilir ve bunlar J (demir-konstantan), T (bakır-konstantan), K (kromel-alümel), E (kromel-konstantan) gibi harflerle gösterilirler. Bu deneyde kullanacağımız ısıl çift K-tipi olarak bilinen kromel-alümel ısıl çiftidir. (-)260-1370 °C aralığında sıcaklık ölçümü yapabilir.

Deneyde Kullanılan Araç ve Gereçler

Bu deneyde kullanacağımız araç ve gereçler şunlardır:

1. Taban levha - 1 adet
2. Çevirme kolu - 1 adet
3. Dinamometre (10 N ve 100 N) - 2 adet
4. Dinamometre askısı - 1 adet
5. Alüminyum sürtünme silindiri - 1 adet (m=390 g, r=2,25 cm)
6. Pirinç (CuZn) sürtünme silindiri - 1 adet (m= 1280 g, r=2,25 cm)
7. Pirinç (CuZn) sürtünme silindiri - 1 adet (m= 640 g, r=2,25 cm)
8. Isıl çift (kromel-alümel) - 1 adet
9. Dijital sıcaklık göstergesi - 1 adet
10. Kütle (m=5 kg ve m=1 kg) - 2 adet
11. Sürtünme band - 1 adet
12. Isıl iletken pasta - 1 adet
13. Kenetleme vidaları - 2 adet

Deney Düzeneğinin Kurulması

Bu bölümde farklı sürtünme silindirlerini kullanarak ısının mekanik eşdeğerini ve silindirlerin öz ısı kapasitelerini hesaplayacağız. Taban levhasını masanın köşesine gelecek şekilde yerleştiriniz. Kenetleme vidasını uygun bölmeye ayarlayınız. Daha sonra kenetleme vidasını taban levhasına sıkıca tutturunuz. Taban levhasının çevirme kolunu takmak üzere hazırlayınız. Taban levhasının çevirme kolunu vidasını kullanarak takınız. Dinamometre askısını tutarak takınız. Dinamometre askısını gerdirerek takınız. Pirinç sürtünme silindirini (m = 1280 g) dönme miline vidalı kısmı gelecek şekilde ayarlayınız. Pirinç sürtünme silindirini monte ediniz. Sürtünme silindirini deney esnasında bir peçete ile tutunuz.

Aksi halde vücudunuzla silindir arasındaki ısı alışverişi neticesinde silindirin sıcaklığı değişebilir. Sürtünme bandının ucundaki ipi tutunuz. İpi dikkatli bir şekilde kütleye takınız. Sürtünme bandını tutunuz. Silindir üzerine üst üste gelmeyecek şekilde 2-3 tur sarınız. Kütleyi tutarak, sürtünme bandının diğer ucunu dinamometreye takınız. Kütleyi yerden 3-4 cm’den daha yükseğe kaldırmayınız. Aksi halde kol bırakıldığında geri dönmeye başlar ve sizlere zarar verebilir. Kütle için uygun mesafeyi ayarlayabilmek için gerekirse sürtünme bandını birkaç kez daha sarınız veya bir sarımı çıkarınız. Isıl çiftin sarı soketini dijital sıcaklık göstergesindeki yuvaya takınız. Dijital sıcaklık göstergesini “ON” tuşuna basarak açınız. Dijital sıcaklık göstergesindeki “C” tuşuna basarak °C ölçeğini seçiniz. Sıcaklık duyarlılığını ilgili tuşa basarak 0,1 °C olacak şekilde ayarlayınız.

Deneyin Yapılışı

Isıl çifti plastik ucundan tutarak metal ucunu ısıl iletken pastaya daldırınız. Bunu, ısıl kontağı iyileştirmek için yapıyoruz. Isıl çiftin metal ucunu sürtünme silindirindeki yuvaya yerleştiriniz ve en az 1 dk bekledikten sonra göstergeden okunan değeri “Kelvin” biriminde çizelgeye T1 olarak kaydediniz. Isıl çifti çıkarınız. Çevirme kolunu saat yönünde hızlı bir şekilde 400 tur çeviriniz. Çevirme esnasında dinamometrenin üzerindeki gerginliğin azaldığına dikkat ediniz. Bu esnada dinamometredeki kuvveti FD olarak çizelgeye kaydediniz. Isıl çifti tekrar silindirdeki yuvaya yerleştirerek sıcaklık sabitlenene kadar bekleyiniz ve sıcaklık göstergesindeki değeri “Kelvin” biriminde T2 olarak kaydediniz.

Deneyin pirinç sürtünme silindiri ile ilgili kısmını tamamladıktan sonra alüminyum silindir ile aynı ölçümler tekrar ediniz. Bunun için öncelikle, kütleyi hafifçe kaldırınız. Sürtünme bandını dinamometreden ve silindirden çıkarınız. Pirinç sürtünme silindirini çıkarınız. Alüminyum sürtünme silindirini takınız. Bir önceki kısımda anlatılanları dikkate alarak kütle, dinamometre ve sürtünme bandı bağlantılarını yapınız. Alüminyum silindiri kullanırken sürtünme 10 N’u geçmemelidir. Bu nedenle 1 kg’lık kütleyi ve daha hassas olan 10 N’luk dinamometreyi kullanınız. Böylece sürtünme bandındaki olası aşınmadan kaçınmış oluruz. Isıl çifti kullanarak ve en az 1dk bekledikten sonra göstergedeki değeri “Kelvin” biriminde T1 olarak kaydediniz. Çevirme kolunu saat yönünde hızlı bir şekilde 400 tur çeviriniz. Çevirme esnasında dinamometrenin üzerindeki gerginliğin azaldığına dikkat ediniz. Bu esnada dinamometredeki kuvveti FD olarak kaydediniz. Isıl çifti tekrar silindirdeki yuvaya yerleştirerek sıcaklık sabitlenene kadar bekleyiniz ve sıcaklık göstergesindeki değeri “Kelvin” biriminde T2 olarak kaydediniz. Deneyin alüminyum sürtünme silindiri ile ilgili kısmını tamamladık. Küçük kütleli pirinç silindir ile aynı ölçümler tekrar edilir. Alüminyum sürtünme silindirini çıkarınız. Küçük kütleli pirinç silindiri takınız. ısıl çifti kullanarak sıcaklık göstergesinde okunan değeri 1 dakika bekledikten sonra “Kelvin” biriminde T1 olarak kaydediniz. Çevirme kolunu saat yönünde hızlı bir şekilde 400 tur çeviriniz. Çevirme esnasında dinamometrenin üzerindeki gerginliğin azaldığına dikkat ediniz. Bu esnada dinamometredeki kuvveti FD olarak kaydediniz. Isıl çifti tekrar silindirdeki yuvaya yerleştirerek sıcaklık sabitlenene kadar bekleyiniz ve sıcaklık göstergesindeki değeri “Kelvin” biriminde T2 olarak kaydediniz. Deneyde alacağımız ölçümler bitmiştir. Deney düzeneğini bozunuz. Dijital sıcaklık göstergesini “OFF” tuşuna basarak kapatınız. Isıl çifti yuvasından çıkarınız. Kütleyi, sürtünme bandını ve dinamometreyi çıkartınız. Son olarak sürtünme silindirini ve çevirme kolunu sökerek, masanızı düzenli bir şekilde bırakınız. Deneyimizde silindir üzerine etki eden kuvvetleri göstermektedir. Burada FD dinamometredeki kuvveti, FR sürtünme kuvvetini ve FG silindirin ucuna asılan kütlenin ağırlığını göstermektedir. Bu deneyde sürtünme silindiri döndürüldüğünde, sürtünme bandındaki sürtünme kuvvetine (FR) karşı mekanik bir iş yapılmaktadır. Sistemin hareketi deney esnasında hemen hemen sabit olduğundan, bir tarafta FD ve FR, diğer tarafta ise FG birbirini dengelemelidir. Bunu;

F _R = F _G - F _D

şeklinde ifade edebiliriz. Buna göre sürtünmenin yaptığı işi, bu kuvvetin etkili olduğu mesafe (2?rn) ve FR kullanılarak hesaplanabilir. Bu durumda yapılan mekanik işi;

W = F _R (2?rn) = (F _G – F _D ) (2?rn) = (Mg – F _D ) (2?rn)

olacaktır. Burada g yerçekimi ivmesi (9,8 m/s2), r sürtünme silindirinin yarıçapı ve n ise çevirme kolunun toplam dönme sayısıdır.

Üretilen Isı Miktarının Hesaplanması

Deney esnasında ölçülen sıcaklık değişimleri kullanılarak silindirde sürtünme nedeniyle oluşan ısı;

Q = mc (T ₂ – T ₁ )

ifadesinden hesaplanabilir.

Isının Mekanik Eşdeğerinin Hesaplanması

J, yapılan mekanik işin üretilen ısı miktarına oranına eşittir. Bu değer;

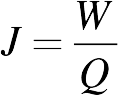
ifadesinden hesaplanabilir.

Öz Isı Kapasitesinin Belirlenmesi

Yapılan mekanik işin tamamen ısıya dönüştüğü düşünüldüğünde;

W = Q = m _cöz ?T

yazılabilir. Buradan öz ısı kapasitesi için denklem yeniden düzenlenirse;

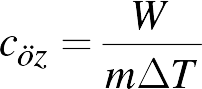
elde edilir.