Portföy Yönetimi Dersi 8. Ünite Özet

Portföy Performanslarının Ölçümü

Bir yatırım kararı alınıp uygulamaya konulduktan sonra o yatırım kararından beklenen sonuçların değerlendirilmesi ve geri besleme mekanizmasıyla yatırım kararının gözden geçirilmesi süreci performans ölçümü olarak adlandırılmaktadır. Performans ölçümü ile portföylerde, görece yatırım başarısını karşılaştırmak ve yorumlamak anlaşılmaktadır. Performans ölçümü veya değerlemesi, portföylerin belli bir dönemdeki performansını başka bir dönem ile ilişkilendirerek veya aynı dönemde farklı portföylerin performansı ile karşılaştırmak sureti ile gerçekleştirilmektedir. Portföyünü yönetmesi için başkasına veren bir yatırımcı, portföyünün ne kadar başarılı yönetildiğini bilmek isteyecektir. Yatırımcıları etkilemek ve müşteri olarak devamlılıklarını sağlamak menkul kıymet ya da portföy yöneticisinin performansına bağlıdır. Portföy yöneticilerinin performansları iyi bir şekilde izlenirse, portföyde yapılabilecek değişiklikler, fon yönetim anlayışı ve yapılan hatalar kolayca ortaya çıkarılabilecek ve daha iyi bir fon yönetimi için gerekli olanların araştırılması mümkün olabilecektir.

İyi bir portföy yönetici kendi performansını değerlendirirken, güçlü ve zayıf yönlerini, geçmişteki başarı veya başarısızlığın şans eseri olup olmadığını tesbit edebilmelidir. Ayrıca, portföyün performansı ayda bir veya üç ayda bir ölçülmelidir.

Performans değerlemesinde iki yaklaşım uygulanmaktadır. Birinci yaklaşım , portföylerin riske göre düzeltilmiş getirilerinin benzer amaçlara sahip olan diğer portföylerin aynı şekilde hesaplanmış getirileri ile ya da o portföyleri en iyi şekilde temsil eden bir gösterge, referans portföyünün (benchmark) getirisi ile karşılaştırılmasından oluşmaktadır. İkinci yaklaşım , portföyde yer alan varlıkların doğru zamanda alınıp doğru zamanda satıldığının test edilmesidir. Portföylerin piyasaya göre performansının değerlendirilmesi için ilgili portföyü amaç ve yapı bakımından en iyi şekilde temsil edecek bir karşılaştırma ölçütünün (benchmark) tespit edilmesi gerekmektedir. Piyasa endeksleri yatırım stratejileri için sıklıkla kullanılan karşılaştırma ölçütleridir. ABD’deki sermaye piyasalarında yatırımcının, verilerine kolaylıkla ulaşabildiği standardize edilmiş piyasa endekslerine; pay senetleri için S&P 500, Wilshire 5000 ve Russell 2000 endeksleri, sabit getirili menkul kıymetler için ise Lehman Brothers Government/Corporate/Aggregate, Salomon Brothers Broad Investment Grade, Merrill Lynch Master endeksleri örnek olarak verilebilir. Türkiye için ise örneğin Borsa İstanbul’de işlem gören şirketlerin pay senetlerinden oluşturulmuş olan bir portföyün performansı, Borsa İstanbul Ulusal 100 Endeksinin aynı dönemdeki getirisi ile karşılaştırılmalıdır.

Oluşturulan portföylerin performanslarının belirli zaman dilimlerindeki getiri oranlarına göre yapılan sıralamalar, portföy yöneticisinin yeteneğini dikkate almamaktadır.

Gerçekte getiri oranlarına göre sıralama yapıldığında bir portföyün pozisyonu;

1. portföyün hedef risk düzeyi,
2. pazarın genel performansı,
3. portföy yöneticisinin beceri düzeyi gibi faktörlere bağlı olmaktadır.

Performans değerlemede en çok bilinen ve uygulama alanına sahip olan riske karşı düzeltilmiş ölçütler; Sharpe oranı, M ² performans ölçütü, Treynor Endeksi, Jensen ölçütü, Değerleme oranı, Sortino oranı ve Fama ölçütüdür.

Sharpe Oranı

Portföy performanslarını ölçmede kullanılan çeşitli tek parametreli risk-getiri ölçütlerinden en çok bilineni 1966 yılında William F. Sharpe tarafından geliştirilen ortalamavaryans modeli çatısı altında portföy performansını değerlendiren bir yaklaşımdır. Sharpe oranı, portföyün standart sapması ile ölçülen risk birimi başına portföyün risksiz getiri oranı üzerinde elde ettiği aşırı getiriyi, portföy performansını taşıdığı riske göre düzelterek ölçmektedir. Yükselen getiri ya da düşen standart sapma Sharpe oranını artırır ve iyi bir durumdur. Bunun tersi durumda ise, düşen getiri ya da artan standart sapma Sharpe oranını düşürmektedir ve bu kötü bir durumdur. Sharpe oranı aşağıdaki şekilde hesaplanmaktadır:

S _p = r _p – r _f / ? _p

Formülde;

S _p = Sharpe oranını,
r _p =Portföy getirisini,
r _f =Risksiz faiz oranını (hazine bonosunun getirisi buna örnek verilebilir),
? _p =Portföyün standart sapmasını göstermektedir.

Formüldeki pay, portföy getirisi ve risksiz faiz oranı arasındaki farkı bu da yatırımcının katlandığı riske karşılık aldığı “ödülü” belirtmektedir. Payda ise, getirilerin standart sapmasını göstermektedir. Bu yüzden oran, her birim değişkenliğe karşılık elde edilen getiriyi belirtmektedir.

M ² Performans Ölçütü

Sharpe oranı, portföy performanslarının sıralanmasında oldukça faydalı olmasına karşın, oranın sayısal değerlerini yorumlamak kolay olmamaktadır. Franco Modigliani ve Leah Modigliani tarafından 1997 yılında geliştirilen ve M -kare veya M ² şeklinde ifade edilen performans ölçütü ile portföy getirilerinin performanslarını yorumlamak daha kolay olmaktadır. M ² ölçütünün temel fikri, tüm portföyleri piyasa karşılaştırma ölçütünün (örneğin S&P 500 veya Borsa İstanbul Ulusal 100 Endeksi) risk seviyesine göre ayarlamak için, riskin piyasa fırsat maliyetini ya da risk ve getiri arasındaki dengeye (getiri elde etmek için belli bir seviyede riske katlanmak ya da riski azaltmak için belli seviyede getiriden vazgeçmek durumunda olmak) dayanmaktadır. M ² ölçütü böylece, uygun niteliklerle, aynı ölçek üzerinde yer alan tüm portföylerin performansları ve portföy yöneticileri hakkında sonuçlara ulaşmaktadır. M ² ölçütü, portföy performansları sıralamasında Sharpe oranı ile aynı sonuçları vermektedir. Ancak, M ² ölçütü, ortalama yatırımcı için anlaşılması ve yorumlanması daha kolay olan bir ölçüttür.

M ² ölçütü aşağıdaki gibi formüle edilmektedir:

M ² = r _p’ – r _m

Burada;

r _p’ = Düzeltilmiş portföyün getirisini,
r _m = Piyasanın getirisini

ifade etmektedir. M ² performans ölçütü, portföyün Sharpe oranı ile pazarın standart sapmasının çarpımına risksiz faiz oranının eklenmesi yoluyla da hesaplanmaktadır.

Treynor Endeksi

Jack L. Treynor’un portföy performanslarını ölçmek için geliştirdiği endeks ile portföy riskini ölçmek için toplam risk göstergesi olan standart sapma yerine, sistematik risk göstergesi olan beta katsayısını seçmiştir. Çünkü menkul kıymet yatırım fonları, çeşitlendirme ve uygun risk gruplarına göre seçilebilme imkânı nedeniyle sistematik olmayan riski elimine edebilmektedirler. Geriye sadece beta tarafından temsil edilen sistematik risk kalmaktadır. Treynor endeksinin formülü şu şekilde gösterilmektedir:

T _p = r _p – r _f / ß _p

Formülde;

r _p = Portföy getirisini,
r _f = Risksiz faiz oranını,
ß _p = Portföy betasını

göstermektedir.

Formüldeki pay, Sharpe oranında olduğu gibi, portföyün getirisi ile risksiz faiz oranı arasındaki farkı ( r _p - r _f ), diğer bir ifadeyle yatırımcının riske katlanması karşılığında elde ettiği toplam ödülü ifade ederken; payda, portföy getirisinin betasını ya da sistematik riskini ifade etmektedir. Dolaysıyla Treynor endeksi, sitematik risk birimi başına ödülü vermektedir. Daha yüksek çıkan Treynor endeksi daha yüksek performansa işaret etmektedir. Portföylerin performanslarına göre sıralandırılmalarında, çoğu zaman Sharpe oranı ve Treynor endeksi benzer sonuçlar vermektedir. Başka bir ifadeyle, iyi bir şekilde çeşitlendirilmiş olan portföylerin sistematik olmayan riskleri ortadan kalkacağından Treynor ölçütü Sharpe ölçütünden çok farklı olmayacaktır. Ancak, bir portföy yeteri kadar iyi çeşitlendirilmemişse, Treynor endeksi çeşitlendirme eksikliğinden kaynaklanan değişkenliğin oranını yakalayamadığı için sonuçlar oldukça farklı çıkacaktır.

Jensen Ölçütü

1968 yılında Michael C. Jensen tarafından geliştirilen, Sermaye Varlıkları Fiyatlama Modeli (SVFM) finansal ekonomistler tarafından riske göre düzeltilmiş getirinin hesaplanmasında bir araç olmuş, portföy performansını ölçmek için kullanılan önemli bir yöntemdir. Jensen ölçütü, portföy performansını tek bir değerle, portföyün ortalama getirisinin Menkul Kıymet Piyasa Doğrusundan sapma derecesiyle ölçmektedir. Bu ölçüt fon getirileri ile pazar getirileri arasında kurulan regresyon denkleminin sabit terimi olan alfa (?) katsayısıdır. Pozitif alfa katsayısı, portföy yöneticisinin başarılı olduğunu, negatif alfa katsayısı ise yöneticinin başarısız olduğunu ifade etmektedir.

Jensen ölçütü SVFM’den elde edildiği için Menkul Kıymet Piyasa Doğrusunu esas alan formülü hatırlamakta fayda vardır: r _p = r _f + ß _p ( r _m – r _f ). Bu eşitlik, herhangi bir menkul kıymetin beklenen getirisinin ( r _p ), risksiz faiz oranı ( r _f ) ile menkul kıymetin sistematik riski ( ß ) ve pazar portföyü üzerindeki risk primi ( r _m – r _f ) toplamına eşit olduğunu göstermektedir. Jensen alfası, portföyün gerçekleşen getirisi ile beklenen getirisi arasındaki fark olarak tanımlandığından dolayı aşağıdaki gibi ifade edilebilir;

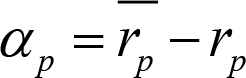
Burada;

? _p = Alfa değerini,
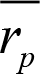= Gerçek getiriyi,
r _p = Beklenen getiriyi

ifade etmektedir.

Değerleme Oranı

Jensen oranı ve Treynor endeksi, portföyün sistematik olmayan riskini göz ardı etmektedir. Bu oranlardaki düzeltmeyi yapmak için portföyün alfasını portföyün sistematik olmayan riskine bölen değerleme oranı geliştirilmiştir. Değerleme oranı aşağıdaki gibi formüle edilmektedir.

Değerleme Oranı = ? _p / ? _up

Formülde;

? p = Portföyünün Jensen alfasını,
? _up = Portföyün sistematik olmayan riskini

ifade etmektedir.

Sortino Oranı

En çok kullanılan risk ölçülerinden biri varyanstır. Varyans bir yatırımın getirilerinin yatırımın ortalamasından sapmalarının karesini ifade etmektedir. Varyansı hesaplarken yukarı/pozitif ve aşağı/negatif yönde herhangi bir kısıtlama yapılmamıştır. Bu yüzden, aylık %-5 ve %+5 getirilere sahip olan bir yatırım, bir ay sabit ve bir sonraki ay %+10 getiriye sahip olan bir diğer yatırımla aynı varyansa sahip olacaktır. Bilindiği gibi, standart sapma varyansın kareköküne eşittir ve dolayısıyla, Sharpe oranı, riski ayarlamak için oynaklığı ölçmede dolaylı olarak taraflı bir ölçü olan standart sapmayı kullandığından bu soruna çözüm bulmak için Sortino oranı geliştirilmiştir. Sortino oranı aşağıdaki şekilde hesaplanmaktadır:

SO = r _p – r _f / ? _d

Formülde;

r _p = Portföy getirisini,
r _f = Risksiz faiz oranını,
? _d = Kısmi standart sapmayı

ifade etmektedir.

Sortino oranında risk ölçüsü olarak standart sapma yerine “minimum kabul edilebilir getiri” olan MAR (Minimal Acceptable Return-MAR)’ın altında kalan getiri sapmalarını ölçen kısmi standart sapmanın kullanıldığı görülmektedir. Birçok yatırım kararında, bazı belirlenen hedefleri gerçekleştirmek için minimum düzeyde kazanılması gereken bir getiri seviyesi vardır. Bu, oluşan bazı kötü sonuçlardan korunmak için minimum seviyede kazanılması gereken getiridir ki “minimum kabul edilebilir getiri” olarak adlandırılmaktadır. Başka bir ifadeyle, minimum kabul edilebilir getiri oranı, yatırımcının elde etmeyi beklediği, garanti edilmiş, riski olmayan getiri oranıdır. Bunun için genelde risksiz faiz oranı kullanılmaktadır.

Fama Ölçütü

Eugene F. Fama (1972) portföy performansını, toplam risk primi karşısında beklenen getirinin üzerinde elde edilen fazla getiri ile ölçmüştür. Fama ayrıca portföy performansının yöneticinin seçicilik ve zamanlama yeteneğine bağlı olduğunu belirtmiştir. Fama’nın geliştirdiği ölçüt aşağıdaki şekilde ifade edilmektedir:

F _p = ( r _p - r _f ) – ( ? _p / ? _rm ) . ( r _m - r _f )

Burada;
r _p = Portföy getirisini,
r _f = Risksiz faiz oranını,
r _m = Karşılaştırma ölçütünün getirisini,
? _p = Portföyün standart sapmasını,
? _rm = Karşılaştırma ölçütünün standart sapmasını,
F _p = Fama ölçütü değerini

ifade etmektedir.

Pozitif Fama ölçütü değeri, portföyün beklenen getirinin üzerinde getiri sağladığını ve Sermaye Piyasası Doğrusunun üzerine doğru hareket ettiğini, negatif Fama ölçütü değeri ise portföyün beklenen getirinin altında getiri sağladığını ve Sermaye Piyasası Doğrusunun altına doğru hareket ettiğini ifade etmektedir.

Performans Ölçüm Yöntemlerinin Eleştirisi

Riski esas alan performans ölçüm yöntemlerinin kullanılması durumunda karşılaşılan sorunlar aşağıdaki gibi özetlenebilir:

• Pay senetlerine ilişkin performans ölçüm yöntemleri Sermaye Varlıklarını Fiyatlandırma Teorisinden türetilmiştir. Dolayısıyla söz konusu teoriye ilişkin varsayımların geçerli olmadığı piyasa koşullarında ona dayalı performans işlemlerinin sonuçları da tartışmalı hale gelecektir.
• Piyasa portföyü olarak kabul edilen portföyün temsil yeteneğine ilişkin sorunlar bulunmaktadır.
• Risk ölçütüne ilişkin sorunlar bulunmaktadır. Bazı yazarlara göre beta katsayısı riskin kesin ölçütü değildir. Piyasa portföyü değiştiğinde beta katsayısının değeri ve performans sıralamaları da değişecektir.
• Portföy riski zaman içinde aynı kalmamaktadır.
• Aynı risksiz faiz oranından borç alıp vermenin mümkün olmadığı durumlarda performans sıralaması değişebilmektedir.
• Yöneticinin performansı değerlendirilirken gözlem süresinin düşen ve yükselen piyasa dönemlerini içeren bir periyot olması gerekmektedir.
• Değerleme döneminin çok uzun tutulması durumunda, yöneticinin performansı değerlendirilirken şans ve yeteneğin birbirinden ayrılması gereklidir.
• Sermaye piyasası doğrusuna dayanan çalışmalar yöneticinin sağladığı getiriye nasıl ulaşıldığını gösterememektedir.
• Riskle düzeltilmiş getiri ölçütlerinin kişisel bir kavram olduğu ve kişilerin içinde bulunduğu koşullara göre farklı sonuçlar doğurduğu ileri sürülmektedir.

Piyasa Zamanlaması Ölçüm Teknikleri

Piyasa zamanlaması, yükselen piyasada kazanç elde etmek veya düşen piyasada kayıplardan kurtulmak için portföy içinde yer alan pay senedi veya nakit ağırlıklarının değiştirilmesi stratejisi olarak tanımlanmaktadır. Piyasanın getirileri, risksiz faiz oranından yüksek olduğunda yükselen piyasa, piyasanın getirileri risksiz faiz oranından küçük olduğunda ise düşen piyasa durumu söz konusu olmaktadır. Portföyün performansının ölçülmesinin yanı sıra portföy yöneticilerinin de piyasa zamanlama stratejilerinin başarısını tespit etmesi önem taşımaktadır. Portföy yöneticilerinin stratejileri;

• Piyasadaki değişmelere göre pay senedi gibi riskli varlıklarla bono gibi risksiz varlıklara yatıracakları tutarlarda değişim yapmasıdır. Portföy yöneticisi piyasanın yükseleceğini düşünüyorsa yatırımlarda riskli varlıklara, eğer piyasanın düşeceğini düşünüyorsa yatırımlarda risksiz varlıklara ağırlık verecektir.
• Piyasadaki değişmelere göre ortalama beta değerini değiştirmesidir. Eğer portföy yöneticisi piyasanın düşeceği beklentisine sahipse portföyün ortalama betasını azaltmak için yüksek betaya sahip varlıkları çıkaracak ve düşük betaya sahip varlıkları portföyüne dahil edecektir. Bunun tersi durumda ise daha fazla riskli varlıkları portföye dahil ederek portföyün ortalama betasını yükseltecektir.

Fama’ya göre yöneticilerin tahmin kabiliyeti ikiye ayrılmaktadır. Bunlardan ilki mikro tahmin olarak nitelendirilen, tek tek menkul kıymetlerin fiyat hareketlerinin tahmini, ikincisi ise makro tahmin olarak nitelendirilen piyasanın genel fiyat hareketlerinin tahminidir. Fonu yöneten kişi ilk olarak düşük değerlendiğine inandığı menkul kıymetleri seçecek ve bunları portföyüne ilave edecektir. Daha sonra piyasanın gelecek hareketlerini tahmin ederek bu hareketlere göre portföy bileşimini tekrar gözden geçirecektir. Dolayısıyla bir portföyün performansının değerlendirilmesi sürecinden bahsedildiği zaman doğru bir değerlendirme yapabilmek için hem seçicilik hem de zamanlama kabiliyetlerinin performansa etkilerinin belirlenmesi gerekmektedir.

Kuadratik Regresyon Modeli

Bu modelin temelinde portföyün sistematik riskinin zaman içinde değişken olabileceği görüşü yer almaktadır. Portföy yöneticisi eğer pazarın gelecek seyrini tahmin edebilirse, portföyünde yer verdiği menkul kıymetleri bu tahminine göre değiştirecektir. Portföy yöneticisi piyasanın yükseleceği beklentisine sahipse piyasa ile aynı yönde hareket eden ve en fazla duyarlılığa sahip varlıkları portföye ilave edecektir. Diğer taraftan, piyasanın gerileyeceği beklentisine sahip olduğunda ise, piyasa ile ters yönde hareket eden ve en düşük duyarlılığa sahip varlıkları seçip portföye dâhil edecektir. Model aşağıdaki gibi tanımlanmaktadır:

r p,t – r f,t = ? + ß ( r m,t – r f,t ) + C ( r p,t – r f,t ) 2 + e p,t

Formülde;

r _p,t = Portföyün t dönemindeki getirisini,
r _f,t = Risksiz faiz oranının t dönemindeki getirisini,
? = Alfa değerini,
ß = Portföyün sistematik risk (beta) seviyesini,
r _m,t = Piyasa endeksinin t dönemindeki getirisini,
C = Portföy yöneticisinin piyasa zamanlama kabiliyetini,
e _p,t = Artık getiriyi,

ifade etmektedir.

Kukla Değişkenli Regresyon Modeli

Kukla değişkenli regresyonda portföy performansının sadece pazarın yükselişi ve düşüşüne göre değerlendirilmesi ve her durumda portföyün ayrı bir betaya sahip olması varsayılmaktadır. Buna göre, piyasanın yükselen dönemlerinde ( r _m > r _f ) beta katsayısı cinsinden yüksek riskli varlık yatırımları düşük risklilerden daha fazla getiri sağlarken, piyasanın düşüş dönemlerinde ( r _m < r _f ) de yüksek riskli varlıklar düşük riskli varlıklara göre daha düşük getiriyle karşılaşacaklardır.

Kukla değişkenli regresyon modelinin esasını portföy yöneticisinin sadece piyasanın yönünü tahmin edebildiği, büyüklüğünü ise tahmin edemediği oluşturmakta ve şu şekilde formüle edilmektedir:

r p,t – r f,t = ? + ß ( r m,t – r f,t ) + C [( r p,t – r f,t ) D ] + e p,t

Formülde;

r _p,t = Portföyün t dönemindeki getirisini,
r _f,t = Risksiz faiz oranının t dönemindeki getirisini,
? = Alfa değerini,
ß = Portföyün sistematik risk (beta) seviyesini,
r _m,t = Piyasa endeksinin t dönemindeki getirisini,
C = Portföy yöneticisinin piyasa zamanlama kabiliyetini,
D = Kukla değişkenini,
e _p,t = Artık getiriyi ifade etmektedir.

Formülde “ D ” kukla değişkeni olup, yükselen piyasalar için “bir” sayısına, düşen piyasalar için “sıfır” sayısına eşit olmaktadır. Bu durumda model; Yükselen piyasa için:

r p,t – r f,t = ? + ß ( r m,t – r f,t ) + C [( r p,t – r f,t )*1] + e p,t

Denklemde ( r _m,t – r _f,t ) ortak paranteze alındığında;

r _p,t – r _f,t = ? + ß ( r _m,t – r _f,t ) ( ß + C ) + e _p,t

denklemi elde edilir.

Düşen piyasa için:

r p,t – r f,t = ? + ß ( r m,t – r f,t ) + C [( r p,t – r f,t )*0] + e p,t
r p,t – r f,t = ? + ß ( r m,t – r f,t ) + e p,t

“ C ” katsayısı ise kuadratik regresyon yönteminde olduğu gibi yöneticinin piyasa zamanlama yeteneğini göstermektedir.