Tıbbi İstatistik Dersi 8. Ünite Özet

Korelasyon Ve Regresyon Analizi

Özet
Sorularla Öğrenelim

Korelasyon Kuramı

Korelasyon analizi x ve y gibi herhangi iki sayısal değişken arasındaki ilişkinin yönünü (aynı veya ters yönlü) ve derecesini (kuvvetli veya zayıf) verir. Aralarında ilişki araştırılan değişkenlerden birinde değerler azalırken, diğerinin değerleri de azalıyorsa veya değişkenlerden birinin değerleri artarken diğerinin değerleri de artıyorsa veya değişkenler zıt yönlü değişim gösteriyorsa, bu değişkenler arasında bir ilişki olduğu söylenebilir.

İki değişken aynı yönde birlikte değişiyorlarsa, yani değerleri birlikte artıp birlikte azalıyorlarsa, aralarında pozitif korelasyon var demektir. Verilerin serpilme çizimi oluşturulduğunda doğrusal artan bir grafik elde edilecektir (s:214, Şekil 8.1).

İki değişken ters yönlerde değişme eğilimi gösteriyorlarsa, (x _i ) arttığında (y _i ) azalıyorsa ya da tersi söz konusu ise x ve y değişkenleri arasında negatif korelasyondan söz edilir (s:215, Şekil 8.2).

İki değişken arasındaki korelasyonun yönünü, doğrudan serpilme çizimine bakarak belirleyebiliriz. Ancak, serpilme çiziminin incelenmesi, x ve y değişkenleri arasındaki ilişki hakkında yaklaşık bir fikir verebilir. x ve y değişkenleri arasındaki korelasyonun derecesini tam ve sayısal olarak ölçmek için ise “korelasyon katsayısı” kullanılır. " 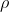$\rho$ " (ro), ana kütle korelasyon katsayısını ifade eder. Bunun belli bir örneklemden kestiricisi (tahmincisi) ise “r” harfiyle gösterilir.

Korelasyon katsayısının alabileceği değerler –1 ve 1 arasında değişir. Korelasyon katsayısının pozitif olması, x ve y arasında pozitif korelasyon, negatif olması ise x ve y arasında negatif korelasyon olduğunu ifade eder. Korelasyon katsayısının +1 ya da –1 değerlerine yakın olması değişkenler arasında çok kuvvetli bir ilişki olduğunu, sıfıra yakın olması ise değişkenler arasında doğrusal bir ilişki olmadığını gösterir.

Ana kütle korelasyon katsayısı,

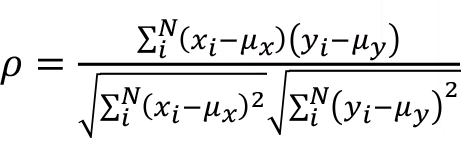
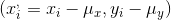$(x_{i}^{,}=x_{i}-\mu _{x},y_{i}-\mu _{y})$ olmak üzere

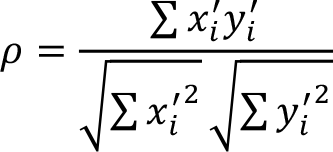
şeklinde belirlenir.

Ancak çoğu durumda ana kütle verileri elde edilemeyeceğinden, örneklem korelasyon katsayısı aşağıdaki gibi hesaplanır:

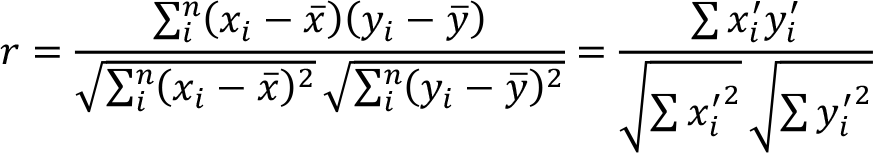
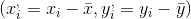
$(x_{i}^{,}=x_{i}-\bar{x},y_{i}^{,}=y_{i}-\bar{y})$

Birçok durumda değişkenler sayısal olarak ölçülemez. Diğer taraftan, bazı durumlarda gözlem değerlerine “sıra numarası“ verilmesi daha uygun olabilir veya gözlem değerleri herhangi bir ölçüte göre zaten sıralanmış olabilir. Değişkenlerin değerleri yerine sıralarının önem kazandığı böyle durumlarda doğrusal korelasyon katsayısı yerine, “sıra korelasyon katsayısı“ (Spearman korelasyon katsayısı) kullanılır.

Sıra korelasyon katsayısının hesaplanmasında gözlemlere büyüklük, önem vb. özelliklerine göre sıra numarası verilir ve gerçek sayısal değerleri yerine bu sıra numaraları arasındaki ilişki belirlenmeye çalışılır. Bazen de veriler zaten sıralanmış olarak elde edilir.

Sıra korelasyon katsayısı aşağıdaki formülle hesaplanır:

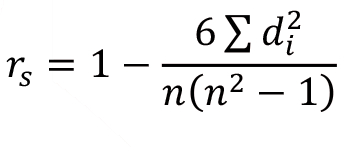
Formülde;
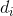$d_{i}$ : sıralamalar arasındaki fark,
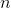: gözlem sayısıdır.

Basit Doğrusal Regresyon Analizi

Korelasyon katsayısı sadece değişkenler arasındaki ilişkinin yönünü ve derecesini vermektedir. Regresyon analizinde ise amaç, önceden belirlenen bağımlı değişken ve bağımsız değişken (değişkenler) arasındaki ilişkiyi matematiksel bir fonksiyonla yazmaktır.

Sonuç niteliğindeki değişken “bağımlı (açıklanan) değişken”, “neden” niteliğindeki değişken ise “bağımsız (açıklayan) değişken” olarak adlandırılır.

Bağımlı değişken “y”, bağımsız değişken de “x” olmak üzere, N birimli bir ana kütle için regresyon denklemi

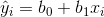
$\hat{y}_{i}=b_{0}+b_{1}x_{i}$

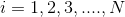
i=1,2,3,....,N

şeklinde yazılır. Bu denkleme “y’nin x’e göre regresyon doğrusu” adı verilir. Denklemdeki;

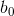$b_{0}$ : Sabit terim (y eksenini kestiği nokta),
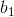$b_{1}$ : Eğim katsayısıdır.

Eğim katsayısı bağımsız değişkendeki bir birimlik değişimin, bağımlı değişken üzerinde artış veya azalış olarak yaptığı etkiyi gösterir.

Genellikle ana kütlenin tamamı gözlemlenemediğinden, n birimlik örneklem seçilerek regresyon doğrusu denklemi “en küçük kareler tekniği” ne göre aşağıdaki gibi tahmin edilir:

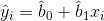
$\hat{y}_{i}=\hat{b}_{0}+\hat{b}_{1}x_{i}$

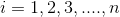
i=1,2,3,....,n

Denklemde;

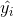$\hat{y_{i}}$ :x ’in belli bir değeri için y’nin kestiricisi,

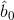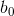$\hat{b}_{0}$ : $b_{0}$ ’ın kestiricisi,

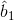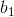$\hat{b}_{1}$ : $b_{1}$ ’in kestiricisidir.

Regresyon doğrusu denklemi için önce eğim katsayısı ( 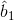$\hat{b}_{1}$ ) değeri aşağıdaki formül kullanılarak belirlenir:

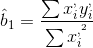
$\hat{b}_{1}=\frac{\sum x_{i}^{,}y_{i}^{,}}{\sum x_{i}^{,^{2}} }$

Eğim katsayısı, “regresyon katsayısı” olarak da isimlendirilir. Daha sonra da sabit terim aşağıdaki gibi hesaplanır:

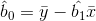
$\hat{b}_{0}=\bar{y}-\hat{b_{1}}\bar{x}$

Değişkenler arasındaki regresyon denklemi belirlendikten sonra, bu denklemin anlamlı olup olmadığının belirlenmesi gerekir.

Bağımsız değişkenin, bağımlı değişkeni açıklama oranı, korelasyon katsayısının karesi olan ve “Belirlilik Katsayısı” olarak isimlendirilen r ² değeridir. Belirlilik katsayısının sınırları 0 ? r ² ? 1 şeklindedir.

Belirlilik katsayısı, bağımsız değişkenin bağımlı değişken üzerindeki etkisi konusunda bir fikir vermekle beraber, bağımsız değişkenin anlamlı (önemli) olduğunu kesin olarak belirtmez. Bunun için eğim katsayısının anlamlılık testi yapılmalıdır. Eğer eğim katsayısı anlamlıysa bağlı olduğu bağımsız değişken bağımlı değişkeni açıklamada önemli bir değişkendir.

Eğim katsayısının anlamlılık sınamaları iki şekilde yapılır. Bunlar z ve t sınamalarıdır. Ancak ana kütle varyansı genellikle bilinmediğinden ve n < 30 olduğundan, t testi uygulanır.

Hipotezler;
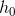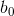$h_{0}$ : $b_{0}$ = 0 (katsayı anlamsız)
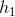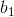$h_{1}$ : $b_{1}$ ? 0 (katsayı anlamlı)

olmak üzere, test istatistiği aşağıdaki gibi belirlenir:

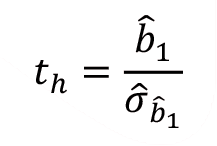
Test istatistiğinin paydasında yer alan değere standart hata kestiricisi denir ve aşağıdaki gibi hesaplanır:

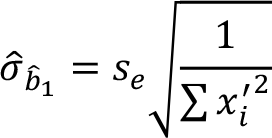
Artıkların standart sapması olan s _e ’nin hesaplanması için aşağıdaki formül kullanılır:

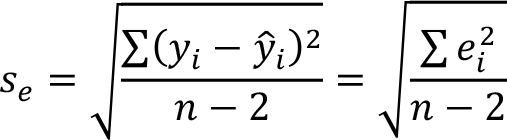
s _e , “tahminin standart hatası” olarak da adlandırılır.

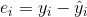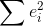e _i , “artık terimi” olarak adlandırılır, bağımlı değişkenin gözlem değerlerinden, regresyon denklemi yardımıyla tahmin edilen değerlerin çıkartılmasıyla elde edilir: $e_{i}=y_{i}-\hat{y}_{i}$ . Artık değerlerinin toplamı daima sıfırdır. Bunların kareleri toplamına ise “artık kareler toplamı” denir ( $\sum e_{i}^{2}$ ).

Test istatistiğinin değeri belirli bir anlam düzeyi ve (n - 2) serbestlik derecesi ile tablo değeriyle karşılaştırılır. Eğer sıfır hipotezi reddedilirse eğim katsayısının anlamlı, yani bağımsız değişkenin bağımlı değişkeni açıklamakta önemli olduğu sonucuna varılır. Belirlenen regresyon denklemi, x ’in çeşitli değerleri için y ’nin alabileceği değerlerin tahmininde kullanılabilir demektir.

Excel Uygulamaları

Excel’de regresyon analizinin yapılabilmesi için “veri çözümleme”nin kurulu olması gerekir. Yeni bir çalışma sayfası açılarak verilerin girilmesinin ardından önce “veri” menüsü, daha sonra da “veri çözümleme” menüsü tıklanır. Karşımıza çıkan pencereden yapmak istediğimiz analiz olan “korelasyon” tıklanır. Daha sonra korelasyonu hesaplanacak değişkenler seçilir ve “Tamam” tıklanarak sonuca ulaşılır.

Regresyon analizi için de, “veri” ve “veri çözümleme” menüsü tıklanır. Karşımıza çıkan pencereden yapmak istediğimiz analiz olan “regresyon” tıklanır. Daha sonra bağımlı değişken “Y Giriş Aralığı”na, bağımsız değişken de “X Veri Aralığı”na girilir. “Tamam” tıklanarak “Özet Çıkışı” olarak belirtilen sonuç tablosuna ulaşılır.

“Özet Çıkışı” olarak ifade edilen sonuçların ne anlama geldiği aşağıda açıklanmıştır:

Çoklu R: r değeridir. (Çoklu R, çoklu korelasyon katsayısı olmasına rağmen, basit korelasyon için de aynı şekilde ifade edilmektedir.)

R Kare: r ² değeridir

Ayarlı R Kare: Düzeltilmiş çoklu belirlilik katsayısıdır ve çoklu regresyon analizinde kullanılır.

Standart Hata: s _e değeridir.

“Katsayılar sütunu”, denklemin sabit terimini ve değişkenlere ait tahmin edilen katsayıları verir.

“Standart hata” sütunu ise katsayılara ilişkin standart hata kestirimlerini verir.

Katsayılar sütunu standart hata sütunundaki değerlere bölündüğünde ise test istatistiği olan t değerleri elde edilir. “F” denklemdeki tüm katsayıların aynı anda anlamlılığı için hesaplanan test istatistiğidir. “P değeri” sütunu ise katsayıların anlamlı olup olmadığını belirtir. 1- P değeri katsayıların % kaç anlamlı olduğunu ifade eder.

Gerçek uygulamalarda ise, bağımlı değişkeni etkileyen çok sayıda bağımsız değişken alınarak analiz yapılır. Bağımsız değişken sayısının iki ve daha fazla olduğu regresyon analizine ise “çoklu regresyon” adı verilir.

Çoklu regresyon analizi için işlemler aynı basit regresyondaki gibidir. Farklı olarak sadece bağımsız değişkelerin her ikisi de (ya da daha fazlası) “X Veri Aralığı”na girilir. “Tamam” tıklanarak “Özet Çıkışı” olarak belirtilen sonuç tablosu elde edilir.

Tıbbi İstatistik Dersi 8. Ünite Özet

Korelasyon Ve Regresyon Analizi

Korelasyon Kuramı

Basit Doğrusal Regresyon Analizi

Excel Uygulamaları

Sosyal Medya'da Paylaş