Yöneylem Araştırması Dersi 5. Ünite Özet

Giriş

Karar verme ortamları farklı şekillerde olabilir. Temel olarak belirlilik, risk ve belirsizlik altında karar ortamlarından söz edilebilir. Parametrelerin değerlerinin bilindiği durumlarda belirlilik, bilinmediği ama tahmin edilebildiği durumlarda risk, hiçbir şekilde değerlerin tahmin edilemediği ortamlarda ise belirsizlik altında karar vermeden bahsedilir. Doğrusal karar problemlerinde belirlilik varsayımı bulunmaktadır.

Duyarlılık analizleri, doğrusal karar problemlerinin çözümü elde edildikten sonra, modelde meydana gelebilecek, parametrelere bağlı veya yapısal değişiklikler karşısında, eldeki en iyi çözümün bundan nasıl etkileneceğini veya eldeki çözümün koruması için parametrelerin hangi aralıklarda değer almaları gerektiğini bulmak amacıyla yapılan analizlerdir.

Simpleks Algoritması’nda Eniyilik ve Uygunluk Koşulları

Simpleks Algoritması’nda önceki bölümlerde de belirtildiği gibi amaç fonksiyonunun enbüyükleme veya enküçükleme olmasına göre, eniyilik koşulunun sağlanıp sağlanmadığı sınanarak problemin çözümüne ulaşıldığı veya bir sonraki aşamanın araştırılması gerektiği sonucuna varılır.

Simpleks Algoritması, aşağıdaki tanımlamalar ışığında ve aşağıda verilen tablo formatında uygulandığında en iyilik koşulları için C _B B ^-1 R-C _R vektörünün değeri dikkate alınır.

X _B : Temel değişkenler vektörü

X _R :Temel olmayan değişkenler vektörü olmak üzere X vektörü aşağıdaki gibi iki parçalı olarak gösterilebilir.

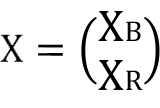
Benzer şekilde; AX = b modelindeki A matrisi ile Enb x ₀ = CX fonksiyonundaki C vektörü de aşağıdaki gibi parçalanabilir :

B : A katsayılar matrisinde temel değişkenlere karşı gelen alt matris

R : A katsayılar matrisinde temel olmayan değişkenlere karşı gelen alt matris

C _B : C katkı vektöründe temel değişkenlere karşı gelen vektör

C _R : C katkı vektöründe temel olmayan değişkenlere karşı gelen vektör iken C = (C _B , C _R ), A = (B,R) şeklinde gösterilebilir.

Simpleks Algoritması, bir temel uygun çözüm (değişkenlerin sıfır veya sıfırdan büyük değer aldığı) ile başlar ve bu çözüm eniyilik koşullarını sağlamıyorsa elde edilen çözümün de temel uygun çözüm olması gerekir. Bu gereklilik ise uygunluk koşulu olarak adlandırılır. Bir başka ifadeyle uygunluk koşulu için de B ^-1 b vektörünün değeri dikkate alınır.

Bir doğrusal karar modelinin eniyi çözümü elde edildikten sonra, amaç fonksiyonunda veya kısıtlarda değişkenlere karşı gelen katsayılarda (C veya R vektörlerinde) olabilecek değişikliklerden, eniyilik koşulları etkilenir. Modelin kısıtlarında yer alan sağ taraf sabitlerinde yani kaynak vektöründe (b) değişiklik olması durumundan ise uygunluk koşulları etkilenir. Bu durumlarda duyarlılık analizi yapmak; bir parametrenin yeni değeri için eniyilik veya uygunluk koşullarının hala sağlanıp sağlanmadığını değerlendirmektir.

Parametrelerde bir değişiklik olmamakla birlikte, modele, yeni bir kısıt veya yeni bir değişken eklemek gibi yapısal değişikliklerle de karşılaşılabilir. Yeni kısıt eklendiğinde bu kısıtın eldeki çözümle sağlanıp sağlanmadığı, yeni değişken eklendiğinde ise, bu değişkenin temele girmeye aday veya eniyilik koşullarını koruyarak temel dışında kalacak bir değişken olma durumlarından hangisine uyduğu araştırılır.

Parametrelere Göre Duyarlılık Analizi

Parametrelere göre duyarlılık analizi katkı parametrelerine, kaynak vektörüne veya teknik katsayılara göre yapılır.

Katkı parametresindeki değişime göre duyarlılık analizi , Verilen bir problemde, katkı parametreleri olan C _B veya C _R değişebilir. Temelde yer alan bir değişkene karşı gelen katkı vektörü (C _B ) değiştiğinde Simpleks Tablo’da x ₀ satırında temel dışı tüm değişkenlere karşı gelen değerler (C _B ^B ₁ R - C _R ) bu durumdan etkilenir. Bu değişiklikler iki türlü olabilir: Parametrenin değerinde belirli bir değişiklik olur ve bu durum analiz edilir veya parametrenin değerinde hangi aralıktaki bir değişim için eldeki çözümün korunacağı (veya değişeceği) belirlenir.

Sağ taraf sabitindeki değişime göre duyarlılık analizi: Bir problemde, sağ taraf sabitleri vektörü, b, değişebilir. Bu durumda Simpleks Tablo’da karar değişkenlerinin değerlerini gösteren B- ¹ b vektörü etkilenir. Simpleks Algoritması bir temel uygun çözümle (temel değişkenler ? değerinde) başlayıp başka bir temel uygun çözüme geçtiğinden, bu değişikliğin uygunluk koşulu olan B ^-1 b? 0 ’ı sağlaması gerekmektedir. Bir başka deyişle, sağ taraf sabitleri de denen kaynak vektöründe bir değişim, eniyilik değil uygunluk koşullarına yansır.

Parametrelere bağlı duyarlılık analizlerinin bir diğer türü de, değişkenlere modelin kısıtlarında karşı gelen teknik katsayılarda değişim olması durumudur. Fakat bir değişkene kısıtlarda karşı gelen katsayının değişmesi, ilgili değişkenin temelde olup olmamasına göre, sırasıyla B veya R vektöründe değişim demektir. Bu durum ise, ya B ^-1 matrisine ya da doğrudan R vektörüne yansıma olup, C _B B ^-1 R – C _R vektörüne ve eniyilik koşullarına yansıyacaktır. Amaç fonksiyonunun durumuna göre, değişimin eniyilik koşullarını koruyup korumadığı veya değişimin hangi aralığı için eniyi çözümün korunacağı bu şekilde bulunabilir.

Teknik katsayılardaki değişime göre duyarlılık analizi , Bir kısıttaki teknik katsayısı değişen bir değişkenin, temelde veya temelde olmamasına göre farklı şekilde analiz edilmelidir.

Temel dışı bir değişkenin bir kısıttaki teknik katsayının değişmesi durumunda R matrisinin söz konusu değişkene karşı gelen vektörü değişeceğinden, bu değişiklik, C _B B ^-1 R – C _R vektörünün sadece ilgili değişkene karşı gelen değerine yansıyacaktır. Yeni durumda, bulunan değerin eniyilik koşullarını hala sağlayıp sağlamadığı araştırılır.

Temelde yer alan teknik katsayının değerinde değişim olması durumu kitabınızın sayfa 101’de örnek ile açıklanmıştır.

Yapısal Değişikliklere Göre Duyarlılık Analizi

Bir doğrusal karar probleminin çözümü elde edildikten sonra, modelde, bazen yapısal değişiklikler olabilir. Bu değişiklikler yeni bir kısıtın veya yeni bir değişkenin eklenmesi şekillerinde görülebilir. Duyarlılık analizleri eniyi çözüm sonrası yapılan analizler olduğundan, yeni bir kısıtın eklenmesi durumunda, eldeki çözümün bu kısıtı da sağlayıp sağlamadığının incelenmesı gerekmektedir. Sağlanıyorsa başka bir işleme gerek olmayıp; yeni kısıt eldeki çözüm için sağlanmıyorsa, bu durumda, bu kısıtı da ekleyip varsa yeni çözüm bulunmalıdır.

Yeni kısıt eklenmesinde, Yeni çözüm gerektiğinde, problem en başından yeni kısıt da dikkate alınarak çözülebileceği gibi; eldeki son tabloya; eşitlik haline getirilmiş yeni kısıtın ve gerekliyse birim matrisin oluşturulması için aylak veya artık değişkenin ve birim matrisin karşı gelen ilgili sütununun eklenmesi sonrasında, problemin çözümüne izleyen ardıştırma ile de devam edilebilir.

Yeni bir değişken eklenmesi durumunda ise şu yol izlenmelidir: Bir karar değişkeni bir çözümde, ya temelde ya da temel dışında yer alır. Bu durumu belirleyen özellik ise ilgili değişkenin temele alınması halinde amaç fonksiyonu değerini daha da iyileştirip iyileştirmeyeceğidir. Değişkene x ₀ satırında karşı gelen değer bu durumun göstergesidir.

Aynı Model Üzerinde Tüm Duyarlılık Analizi Türlerinin Örneklenmesi

Konu kapsamında açıklanan analiz türlerini adım adım nasıl ilerlediğini görmek istersek,

• Verilen problemi eşitlik haline getirmek için gerekli miktarda aylak değişkenler eklenir ve simpleks toblo çözümlenir. Modele başlangıçta eklenen aylak değişkenler olup ilk çözümde birim matrisi ( I ) oluşturmuşlar ve aynı zamanda başlangıç uç noktaya da karşı gelmişlerdir. Öte yandan, gelinen son aşamada, temel dışında olmaları sebebiyle, A matrisinde karşı gelen katsayıları da tanım gereği, temel olmayan değişkenlere karşı gelen katsayılar matrisi olan R’yi vermektedir. Kısacası bu aşamada, R matrisi, aynı zamanda da birim matris olan I matrisi olmakta, bu durumda (I), matris çarpımında etkisiz olduğundan son tabloda B ^-1 R matrisi ile ^B-1 matrisi aynı matris olmaktadırlar.
• Katkı parametrelerinde değişiklik : Temelde yer alan değişkeninin katkı parametresi olan değerinin hangi aralığı için eldeki eniyi çözümün korunacağı bulunmak istensin. Katkı parametresindeki değişim miktarını enbüyüklemek için, eldeki çözümün korunması için 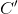_B B ^-1 R - C _R ? 0 özelliğin sağlanması halinde mümkün olmaktadır. Yani temel olmayan değişkenlerin amaç fonksiyonu satırında karşı gelen değerler ? koşulunu sağlamalıdır.
• Sağ taraf sabitlerinde değişiklik: Problemin kısıtlarına karşı gelen kaynak vektöründeki değişiklik, uygunluk koşulu olan B ^-1 b ? 0 yansır.
• Teknik katsayılarda değişiklik: Temelde yer alan değişkenlerin değerindeki değişmesi durumunun Eniyilik koşullarının korunup korunmadığını belirleyebilmek için amaç fonksiyonuna göre koşulların test edilmesini sağlar.
• Yeni kısıt eklenmesi: Gerçek problemler modellendikten ve çözüldükten sonra önceden öngörülemeyen, bulunulan sistemin koşullarında sonradan ortaya çıkabilecek bazı değişiklikler sebebiyle, göz önünde bulundurulması ihtiyacı beliren yeni bir kısıt olabilir. Daha öncede belirtildiği gibi bu durumda, eldeki çözümün yeni kısıtı da sağlayıp sağlamadığı kontrol edilmelidir. Eldeki çözüm yeni kısıtı sağlamadığından, bu kısıtın da probleme eklenerek yeni çözümün araştırılması gerekmektedir.
• Yeni değişken eklentisi: Bazı durumlarda, değişen koşullar sebebiyle, probleme yeni bir değişken eklenebilir. Örneğin üç ayrı ürün üreten bir işletmenin yeni ve dördüncü bir ürünü daha piyasaya sunması durumunda, diğer tüm kaynakların vb. aynı kalıp, artık bu yeni ürününde mevcut kaynakları kullanması, bu durumda eniyi üretim miktarlarının yeniden belirlenmesi gerekliliği bu duruma örnek olarak verilebilir. Bu tür durumlarda yeni karar değişkenleri söz konusu olmaktadır. Temel dışında olup da amaç fonksiyonunu istenen yönde geliştirebilecek durumda ise, temele alınır. Buna göre, eniyi çözüm elde edildikten sonra probleme dahil olan bir değişkenin, temele alınmasına gerek olup olmadığı sorusu yanıtlanmalıdır. Bu soruya yanıt verebilmek için de, ilgili değişkene amaç fonksiyonu satırında karşı gelen değer hesaplanıp, amaç fonksiyonunun enbüyükleme veya enküçükleme olmasına göre yukarıdaki soruya yanıt aranır. Bu değerin hesaplanması için, yeni değişkene problemin kısıtlarında karşı gelen katsayıların yani, yeni değişkenin kaynak kullanım değerlerinin, (R _yeni ) ve amaç fonksiyonundaki birim katkısının (C _yeni ) bilinmesi gerekmektedir