Mathematics 1 Dersi Genel Özet
1 Sets And Numbers
- Özet
Sets
A set is a well-defined collection of elements.
Sets are usually denoted by the letters A, B, C , …, and the elements of the sets are represented by the small letters a, b, c , …. If the element a belongs to the set A , we denote this fact by use of the notation a ? A , if the element a does not belong to A then we write a ? A .
A set can be defined by listing all elements or by giving a rule that determines all the elements of the set. For example,
A = {a, b, c, d}, B = {1, 2, 3, … , 10},
C = {x| x is a natural number grater than 1000},
D = {x| x is a city in Turkey with population
greater than 1 million}
The set A is a subset of the set B , written A ? B , if every element of A is also an element of B . Two sets A and B are equal, written A = B , if both inclusions A ? B and B ? A are satisfied simultaneously.
The set containing no element is called the empty set and is denoted by Ø. The set Ø is a subset of any set.
Example: A = {1, 2, 5} , B = {5, 1, 2} , C = {1, 2, 5, 6} . Then A = B and A ? C .
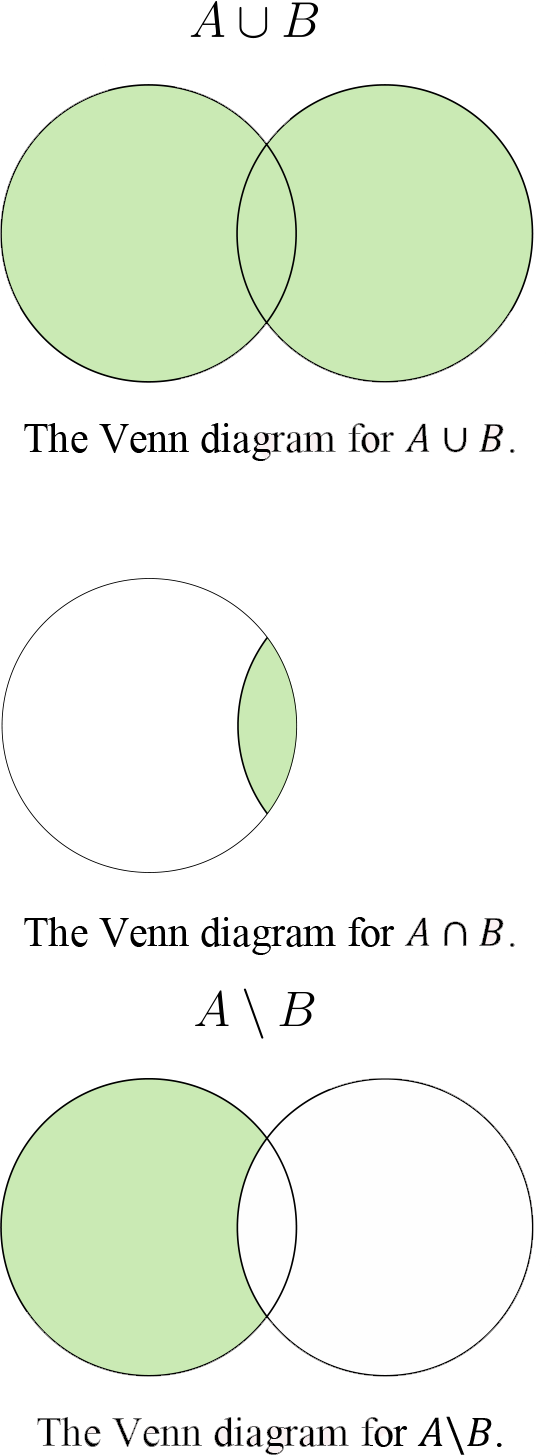
It is important to represent a set by writing its elements inside a closed planar curve. Such a representation is called a Venn diagram.

If in some problems, all the sets under examination are subset of a wider set then this wider set is called a universal set and usually is denoted by U . For example, if in some problem all sets are subsets of the set of natural numbers not greater than 15 then the universal set becomes
U = {1, 2, 3, … , 15}.
- The set A ? B = {x| x ? A or x ? B } is called the union of A and B ,
- The set A ? B = {x| x ? A and x ? B } is called the intersection of A and B ,
- The set A\B = {x| x ? A and x ? B } is called the difference of A and B .
The set A c = U\A is called the complement of A , where U is the universal set.
Example:
A = {1, 3, 5, 7} , B = {3, 5, 9, 10} , U = {1, 2, … , 10} .
Then
A ? B = {1, 3, 5, 7, 9, 10},
A ? B = {3, 5},
A c = {2, 4, 6, 8, 9, 10},
B c = {1, 2, 4, 6, 7, 8}.
A set A is called finite if it contains finite number of elements. Otherwise, it is called an infinite set. For a finite set A , the number of elements in this set is denoted by s(A) . For given finite sets A and B , the equality
s(A ? B) = s(A) + s(B) - s(A ? B)
is true. If A has n -elements then the total number of all subsets is 2 n .
Properties of Set Operations
Set operations have many obvious properties. We list some of them below.
- A ? ( A ? B ), B ? ( A ? B )
- (A c ) c = A
- A ? ( B ? C ) = ( A ? B ) ? ( A ? C )
- A ? ( B ? C ) = ( A ? B ) ? ( A ? C )
- ( A ? B ) c = A c ? B c
- ( A ? B ) c = A c ? B c
Numbers
The most familiar number set is the set N of the natural numbers:
N = {1, 2, 3, 4, … }.
The set of all integers is denoted by
Z = N ? {0} ? {-1, -2, -3, … }.
A quotient of two integers with nonzero denominator is called a rational number. The set of all rational numbers is denoted by Q.
Rational numbers with denominators 10 , 100 , 1000, … are called decimal fractions. For example,
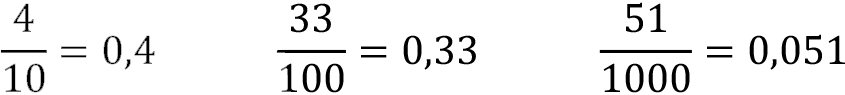
are very simple examples of decimals numbers.
Every rational number has finite or repeated infinite decimal representation. The real line is a line with a fixed scale, origin and direction.
Every rational number has a unique representation on the real line. On the other hand, there are infinitely many points on the real line which cannot be represented by rational numbers. The numbers, corresponding to such points are called irrational numbers. For example, ?2, -?3, ? are irrational numbers.

The union of the sets of rational and irrational numbers is called real numbers and is denoted by R.
Inequalities
Let a ? R and b ? R be real numbers and these numbers correspond the points A and B on the real line. If the point A lies to the left of the point B then it is written as a < b or b > a ( a is less than b or b is greater than a ). If a is not greater than b then it is written as a ? b or b ? a . These relations are called inequalities and below we give the most important properties of inequalities:
- If a < b then a + c < b + c
- If a < b and c > 0 then ac < bc , if a < b and c < 0 then ac > bc.
In order to list fractions in some order (increasing or decreasing) the fractions should be reduced to a common denominator or numerator.
- Given
 the number 32 is a common denominator.
the number 32 is a common denominator.
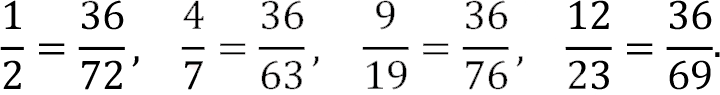
therefore

- Given
 the number 36 is a common numerator
the number 36 is a common numerator
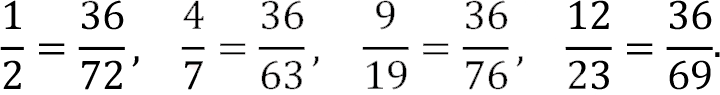
Therefore

Powers and Roots
Given a ? R and n ? N, a to the power of n is defined as
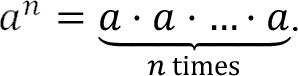
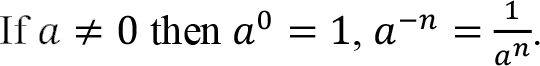
For a given a > 0 , a number b > 0 satisfying the equality b n = a is called the n-th root of the number a and is denoted by 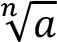 or
or 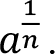 If n = 2 the symbol ?a is used instead of
If n = 2 the symbol ?a is used instead of 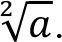 . If n is odd and a ? 0 then by definition
. If n is odd and a ? 0 then by definition 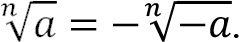 .
.
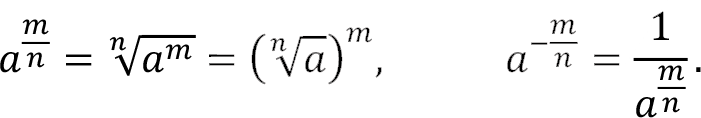
The powers and roots have the following properties. Let p and q be fractions with positive denominators. Then
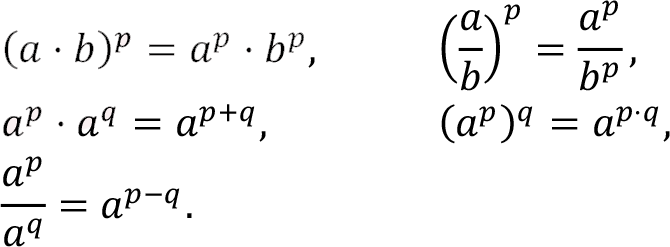
Examples:
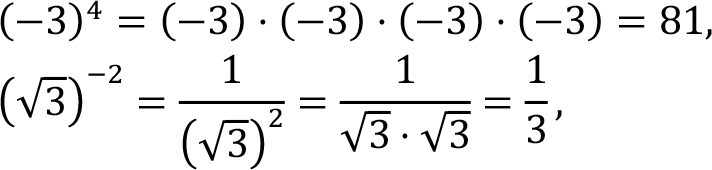
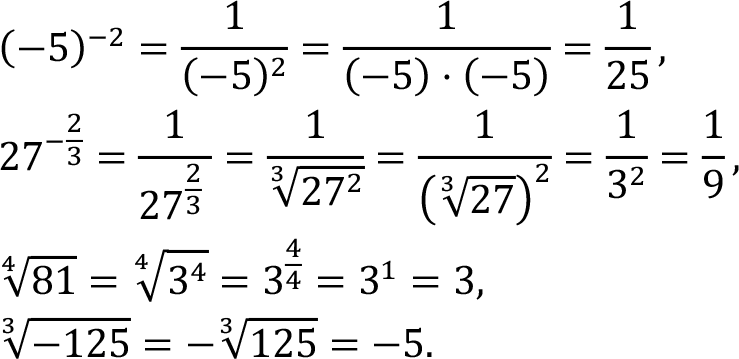
Intervals of Real Numbers
Intervals are subsets of R and are defined as follows:
( a, b ) = { x ? R| a < x < b },
[ a, b ] = { x ? R| a ? x ? b },
( a, b ] = { x ? R| a < x ? b },
[ a, b ) = { x ? R| a ? x < b },
( a, ? ) = { x ? R| x > a },
( -?,b ] = { x ? R| x ? b }.
For example, 0 ? (0,3), 1 ? (0,3), 0 ? [0,3], 2 ? (1, ?), 0 ? (-?, -1),
[0,3] ? [-1,2] = [-1,3], [0,3] ? [-1,2] = [0,2].
The set of all real numbers R is the interval (-?, ?).
The absolute value of a real number a, written |a|, is defined by
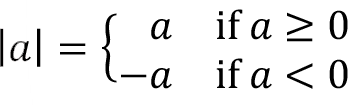
and has the following properties:
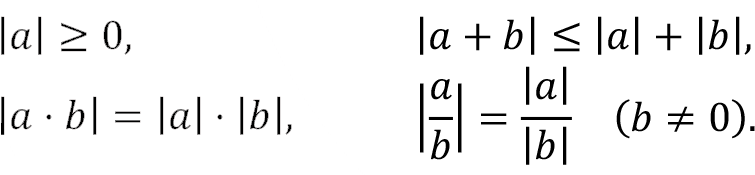
For example, |(-3) · 5| = |-3| · |5| = 3 · 5 = 15 , 
Example: Represent the intervals (4,6), [-2,2] by using the absolute value.
Solution. The middle point of [4,6] is  the length is 2, therefore
the length is 2, therefore
(4,6) = {x ? R| |x - 5| < 1}.
The middle point of [-2,2] is 0, the length is 4, therefore
[-2,2] = {x ? R| |x| ? 2}.