Mathematics 1 Dersi 2. Ünite Özet
Functions And Their Graphs
- Özet
- Sorularla Öğrenelim
Functions and Their Graphs – Review
Let A and B be two sets different than the empty set. A correspondence assigning each element of the set A , one and only one element of the set B is called a function from the set A into the set B . Functions are generally denoted by the lower case letters such as f, g, h. In this case a function defined from the set A to the set B is denoted by 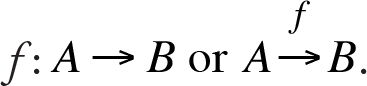 In this context, the set A is called the domain of the function, and the set B is called the range set.
In this context, the set A is called the domain of the function, and the set B is called the range set.
For a given function f and an element a from its domain A , the element corresponding to a under the rule f is called the image of the element a , and is denoted by f(a) .
Example: Let the function f: R › R , f( x ) = 2 x + 6 be given. Let find the numbers f(1) and f(-1) . If we write 1 instead of x in the rule of f then it holds,
f (1) = 2 · 1 + 6 = 7.
If we write -1 instead of x in the rule of f then, we obtain the image of -1 under the function f as
f (-1) = 2 · (-1) + 6 = -2 + 6 = 4.
For the function f: A › B , the set of the images for every elements in A is called the image (range) of f and is denoted by f( A ) . Symbolically we have
f ( A ) = { f (a) | a ? A }.
In order two functions to be equal the domains, the images, and the rules of these functions must be the same. In terms of mathematical notation, given two functions f: A › B and g: C › D , if A = C , B = D , and for all x ? A , f( x ) = g( x ) then the functions f and g are said to be equal , and this equality is denoted by f= g . For example the functions f : N › R , f ( x ) = x 2 + 1 and g: R › R , g( x ) = x 2 + 1 are not equal since their domains are not same although the ranges the rules are the same.
If a rule defining a function is given but the domain has not been specified explicitly, then the largest set which makes the rule meaningful is understood. This set is denoted by D f and is called the natural domain of the function. For instance, the function given by the rule 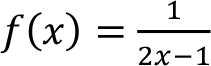 makes sense if its denominator is not zero, i.e. 2 x - 1 ? 0 should be satisfied. Thus, the domain D f is should be taken as
makes sense if its denominator is not zero, i.e. 2 x - 1 ? 0 should be satisfied. Thus, the domain D f is should be taken as 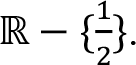 .
.
Consider the function f: A › B . For every x 1 , x 2 ? A if x 1 ? x 2 implies f ( x 1 ) ? f ( x 2 )
then the function f is called one-to-one (or injective). Equivalently, to confirm the one-to-oneness of a function it will be enough to show that f ( x 1 ) = f ( x 2 ) whenever x 1 = x 2 . That is, if the images of two different elements from the domain under the action of f are also different, such functions are called one-to-one .
If the image is equal to the range, i.e. f( A ) = B the function f is called surjective (onto) .
If a function which is both one-to-one and onto is called a bijection . As an example, consider f : R › R , f( x ) = x + 1.
Types of the Function
- For every element a from the domain A , and c ? B , if f (a) = c , the function f is called constant .
- The function from A to A assigning every element of A to itself is called the identity function . The identity function is generally denoted by I or if the domain needs to be specified by I A . In this case, we write
I A : A › A ,I(a) = a
- Functions, which are represented by different formulas on different subsets of its domain are called piecewise defined functions. As a piecewise defined function, absolute value is represented as
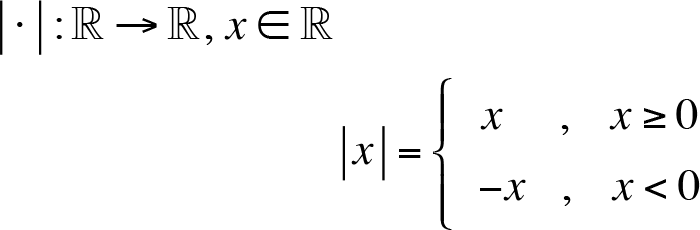
Example: f : R › R ,
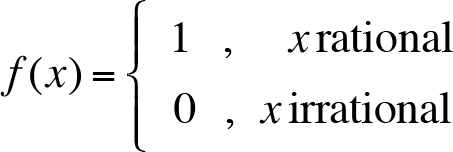
is called Dirichlet function.
Composites of Functions
Let the functions f: A › B and g: B › C be given. The function g ° f: A › C , defined by the rule
(g ° f )( a ) = g( f ( a ))
is called the composition of the functions f and g.
Example: Consider the functions f: R › R , f( x ) = 2 x + 4 and g : R › R , g ( x ) = 3 x - 1. Let us now find the composition g ° f :
For g ° f: R › R , using the definition we obtain
(g ° f )( x ) = g ( f ( x ) ) = g(2 x + 4) = 3(2 x + 4) - 1 = 6 x + 11
Inverse Function
Let the bijective function f: A › B be given. The inverse of f is defined as
f -1 : B › A , f -1 ( y ) = x
Here, x is the one and only element that satisfies the equality f(x)=y .
Operations on real valued functions: Given the functions f : A ? R › R and g : A ? R › R , the addition, subtraction and multiplication of these functions are defined as
f + g: A › R , ( f + g)( x ) = f ( x ) + g( x )
f - g: A › R , ( f - g)( x ) = f ( x ) - g( x )
f · g: A › R , ( f · g)( x ) = f ( x ) · g( x )
A little more care has to be taken defining the division. Since it is not allowed to divide by zero, the function in the denominator must not be zero for the definition to make sense. Therefore, if for every element a ? A , g(a) ? 0 then the division of f and g is defined as

We may define, also, multiplication by a constant. Assuming c ? R , we define
c · f: A › R , ( c · f)( x ) = c · f( x )
Graphs of Functions
We now introduce the Cartesian coordinate system, a tool which enables us to plot the graphs of functions.
We call the set of ordered pairs of real numbers the product of R by itself. We denote it by
R × R = R 2 = {( x , y )| x , y ? R }.
The first element x of the ordered pair ( x, y ) is called the first component of the ordered pair, and the second element y is called the second component.
Two real lines intersecting perpendicularly at both their zeros constitutes the Cartesian coordinate system . In this system, the horizontal real line is called the x -axis, or abscissa, and the vertical real line is called the y -axis, or ordinate. We call the point of intersection of the number lines as the origin.
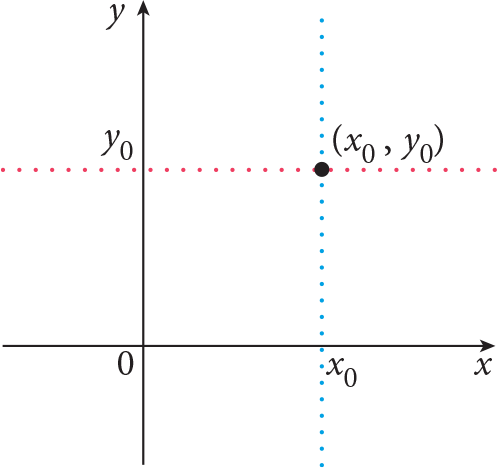
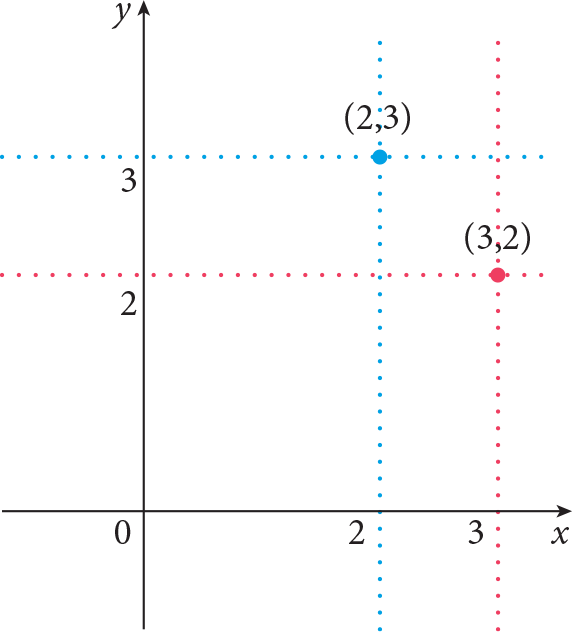
| A point represented by ordered pair (x 0 , y 0 ) in the Cartesian coordinate system | The points represented by ordered pair (2, 3) and (3, 2) in the Cartesian coordinate system |
Let f : A ? R › R be given. The graph of the function f is denoted by G f and defined as the following set:
G f = {(x,f(x)) | x ? A }.
Example:
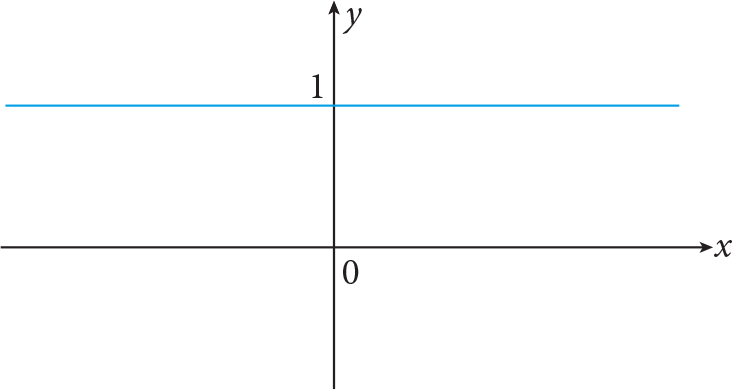
The graph of the function f : R › R , f ( x ) = 1.
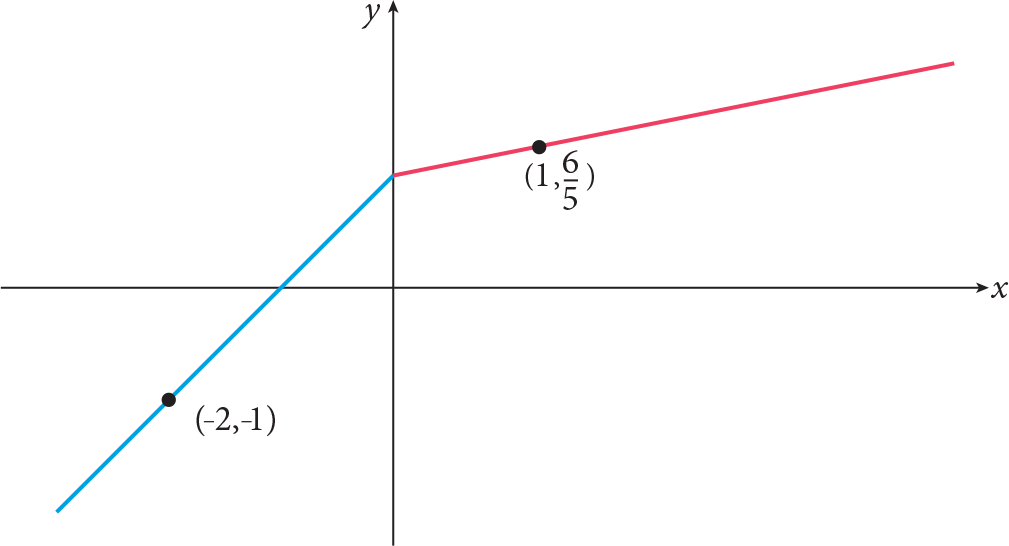
The graph of the piecewise function is denoted by x +1 for x <0 and 1+ x /5 for x ?0 on R.