Tıbbi İstatistik Dersi 7. Ünite Özet
İstatistiksel Tahmin Ve Hipotez Testleri
- Özet
- Sorularla Öğrenelim
İstatistiksel Tahmin
Bir ana kütle parametresinin değerinin örneklem istatistiğinden yararlanarak belirlenmeye çalışılması istatistiksel tahmindir.
Nokta (Tek Değer) Tahmin: Ana kütle parametresini çekilen örneklemden elde edilecek örneklem istatistiğinden hareketle tek bir değerle tahmin etmek nokta tahmin (tek değer tahmin) olarak adlandırılır. Genel gösterim olarak ana kütle parametresi “? ” , örneklem istatistiği ise “T” simgeleri ile gösterilecektir. Nokta tahmininde genel olarak ana kütle ortalaması, ana kütle oranı ve varyans tahmini yapılır. Bu tahminlerde kullanılacak eşitlikler sırasıyla aşağıdaki gibi gösterilebilir.
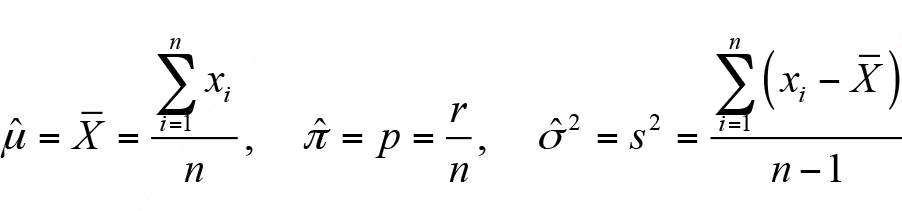
Başarılı bir nokta tahmininin sapmasızlık, tutarlılık, etkinlik ve yeterlilik özelliklerini sağlaması gerekir. Sapmasızlık, örneklem istatistiğinin beklenen değerinin tahmin edilmek istenen ana kütle parametre değerine eşit olmasıdır. E ( 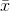 ) = µ eşitliği sağlanıyorsa örneklem ortalaması ana kütle ortalamasının sapmasız bir tahmincisidir, aksi durumda tahmin yanlıdır. Örneklem hacmi n, ana kütle hacmine yakın olacak şekilde arttırıldığında, tahmin değeri ile ana kütle parametresi arasındaki fark sıfıra yaklaşıyorsa tahmin değeri tutarlıdır. Etkinlik tahminlerin örnekleme dağılımının varyansı ile ilgili olup, bir ana kütle parametresi için alternatif tahminler arasında varyansı en küçük olan etkindir. Yeterlilik özelliği tahmin değerinin hesaplanmasında örneklem verilerinin tamamının kullanılıp kullanılmadığı ile ilgili olup, örneklem değerlerinin tamamının kullanılması ilgili tahminin yeterli olduğunu göstermektedir.
) = µ eşitliği sağlanıyorsa örneklem ortalaması ana kütle ortalamasının sapmasız bir tahmincisidir, aksi durumda tahmin yanlıdır. Örneklem hacmi n, ana kütle hacmine yakın olacak şekilde arttırıldığında, tahmin değeri ile ana kütle parametresi arasındaki fark sıfıra yaklaşıyorsa tahmin değeri tutarlıdır. Etkinlik tahminlerin örnekleme dağılımının varyansı ile ilgili olup, bir ana kütle parametresi için alternatif tahminler arasında varyansı en küçük olan etkindir. Yeterlilik özelliği tahmin değerinin hesaplanmasında örneklem verilerinin tamamının kullanılıp kullanılmadığı ile ilgili olup, örneklem değerlerinin tamamının kullanılması ilgili tahminin yeterli olduğunu göstermektedir.
Aralık Tahmini: Ana kütle parametresinin değerinin örneklem istatistiğinden yararlanarak bir aralık biçiminde tahmin edilmesine aralık tahmini denir. Belirlenen aralığa güven aralığı, bu aralığın alt ve üst sınır değerlerine güven sınırları denir. Aralık tahmini, tahminin doğruluğundan ne kadar emin olunacağını gösteren belirtilen bir olasılık düzeyine göre hesaplanır. Yani hesaplanan güven aralığının ana kütle parametresini içermesi olasılığı (1-? ) olup bu olasılık değeri güven düzeyi olarak adlandırılmaktadır. Burada ? tahminin hata payını ifade etmektedir.
Ana Kütle Parametresinin Aralık Tahmini
Ana kütle parametresinin güven sınırlarının belirlenmesi için ilgilenilen örneklem istatistiğinin örnekleme dağılımının bilinmesi gereklidir. İlgili ana kütle parametresinin güven sınırları genel olarak,
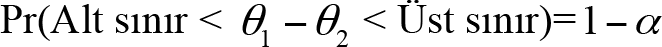
şeklinde ifade edilebilir.
Ana Kütle Ortalaması µ’nün Aralık Tahmini: µ ' nün aralık tahmini örneklem hacmine bağlı olarak büyük örneklemler (n>30) ve küçük örneklemler (n<30) için ayrı ayrı ele alınacaktır.
Büyük Örneklemler İçin µ ’nün Aralık Tahmini:
n>30 olduğunda ana kütle ortalaması olan µ ' nün aralık tahmini
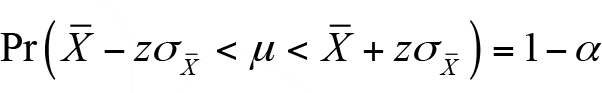
şeklindedir. Burada z değeri başlangıçta belirlenen güven düzeyine karşılık gelen standart normal eğri alanları tablosundan bulunacak değerdir. Ana kütle standart sapması bilindiğinde, örneklem ortalamasının standart hatası,
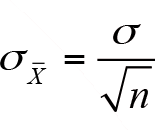
yardımıyla hesaplanır. Uygulamada genellikle ana kütle standart sapması bilinemez ve onun yerine örneklem standart sapması “s” kullanılır.
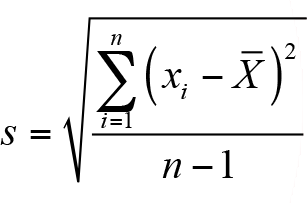
Bu eşitlik kullanılarak ortalamanın standart sapmasının tahmini,
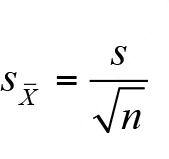
Yardımıyla hesaplanır. Dolayısıyla ana kütle ortalaması için aralık tahmini,
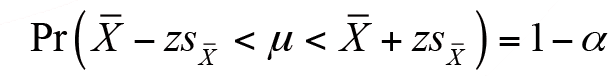
eşitliğinden elde edilir.
Küçük Örneklemler İçin µ ’nün Aralık Tahmini: Ana kütle aritmetik ortalaması µ için aralık tahmini
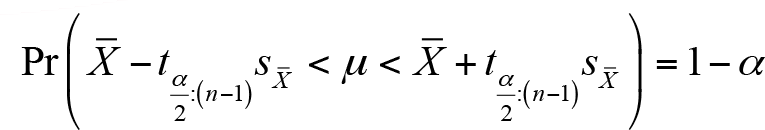
eşitliğinden yararlanarak elde edilir. Burada t değeri küçük örneklem durumunda kullanılan Student-t dağılımının kritik değer tablosundan ilgili güven düzeyi ve n-1 serbestlik derecesi dikkate alınarak bulunur.
Ana Kütle Parametreleri Arasındaki Farkın Aralık Tahmini
Anakütle parametreleri arasındaki farkın aralık tahmini genel olarak
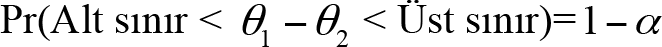
Şeklinde gösterilebilir. Burada ?1 ve ? 2 iki farklı ana kütlenin parametreleridir.
Ana Kütle Ortalamaları Arasındaki Farkın ( 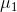 -
- 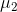 ) Aralık Tahmini: Ortalamalar arasındaki farkın aralık tahmininde de örneklemin büyük ya da küçük olma durumu dikkate alınacaktır.
) Aralık Tahmini: Ortalamalar arasındaki farkın aralık tahmininde de örneklemin büyük ya da küçük olma durumu dikkate alınacaktır.
Büyük Örneklemler İçin 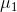 -
- 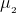 ’nin Aralık Tahmini:
’nin Aralık Tahmini:
n>30 olduğunda ana kütle ortalaması olan µ ' nün aralık tahmini
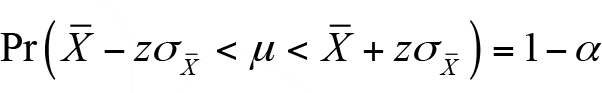
şeklindedir. Burada z değeri başlangıçta belirlenen güven düzeyine karşılık gelen standart normal eğri alanları tablosundan bulunacak değerdir. Ana kütle standart sapması bilindiğinde, örneklem ortalamasının standart hatası,
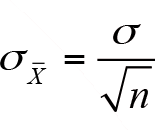
yardımıyla hesaplanır. Uygulamada genellikle ana kütle standart sapması bilinemez ve onun yerine örneklem standart sapması “s” kullanılır.
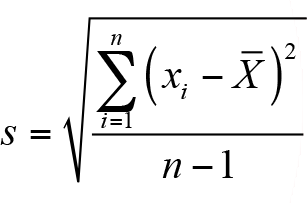
Bu eşitlik kullanılarak ortalamanın standart sapmasının tahmini,
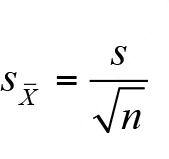
Yardımıyla hesaplanır. Dolayısıyla ana kütle ortalaması için aralık tahmini,
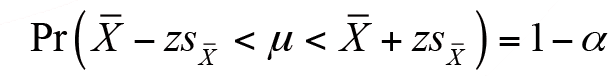
eşitliğinden elde edilir.
Küçük Örneklemler İçin µ ’nün Aralık Tahmini: Ana kütle aritmetik ortalaması µ için aralık tahmini,
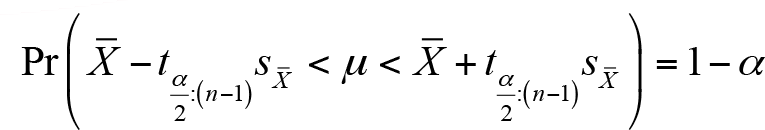
eşitliğinden yararlanarak elde edilir. Burada t değeri küçük örneklem durumunda kullanılan Student-t dağılımının kritik değer tablosundan ilgili güven düzeyi ve n-1 serbestlik derecesi dikkate alınarak bulunur.
Ana Kütle Parametreleri Arasındaki Farkın Aralık Tahmini
Anakütle parametreleri arasındaki farkın aralık tahmini genel olarak
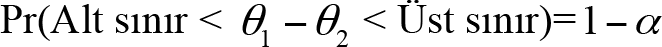
Şeklinde gösterilebilir. Burada ?1 ve ? 2 iki farklı ana kütlenin parametreleridir.
Ana Kütle Ortalamaları Arasındaki Farkın ( 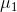 -
- 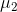 ) Aralık Tahmini: Ortalamalar arasındaki farkın aralık tahmininde de örneklemin büyük ya da küçük olma durumu dikkate alınacaktır.
) Aralık Tahmini: Ortalamalar arasındaki farkın aralık tahmininde de örneklemin büyük ya da küçük olma durumu dikkate alınacaktır.
Büyük Örneklemler İçin 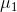 -
- 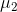 ’nin Aralık Tahmini:
’nin Aralık Tahmini:
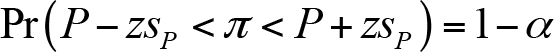
Eşitliği yardımıyla hesaplanabilir. Buradaki ortalama farklarının standart hatası 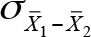 ana kütle standart sapmaları bilinmesi halinde,
ana kütle standart sapmaları bilinmesi halinde,
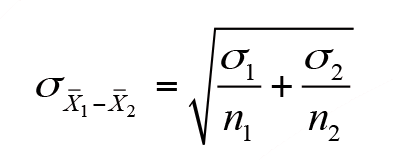
şeklinde hesaplanır. Ana kütle standart sapmalarının bilinmediği durumda standart sapmaların tahmincileri olan örneklem standart sapmaları “s 1 ve s 2 ” kullanılarak ortalamalar arası standart hatanın tahmini,
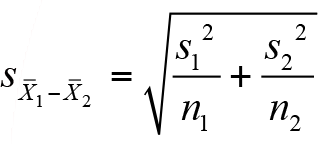
olarak hesaplanır ve buna göre ortalamaların farkı için aralık tahmini aşağıdaki gibi ifade edilir.
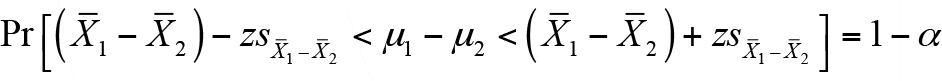
Küçük Örneklemler İçin 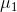 -
- 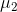 ’nin Aralık Tahmini: Örneklem hacimlerinin küçük olması durumunda (n1, n2<30 ) ana kütle ortalamaları arasındaki farkın aralık tahmini,
’nin Aralık Tahmini: Örneklem hacimlerinin küçük olması durumunda (n1, n2<30 ) ana kütle ortalamaları arasındaki farkın aralık tahmini,
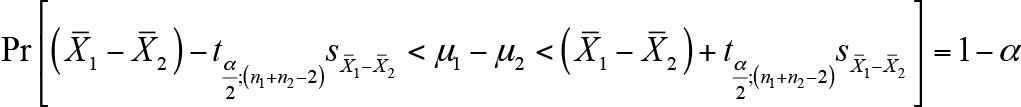
yardımıyla elde edilir. ? ? Burada t değeri küçük örneklem durumunda kullanılan Student-t dağılımının kritik değer tablosundan ilgili güven düzeyi ve n 1 +n 2 -2 serbestlik derecesi dikkate alınarak bulunur.
Yukarıda verilen güven aralığındaki ortalamalar arasındaki farkın standart hatasının tahmini,
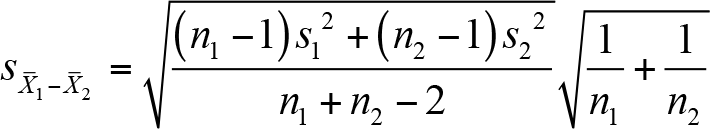
eşitliğiyle hesaplanır.
Ana Kütle Oranı ?’nin Aralık Tahmini: Örneklem oranı p kullanılarak, örneklem hacminin yeterince büyük olduğu durumlarda (n 1 , n 2 >30 ), ana kütle oranı ? için aralık tahmini aşağıdaki güven sınırlarıyla yapılabilir:
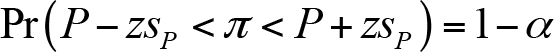
Eşitlikte bulunan oranın standart hatasının tahmini Ps ,
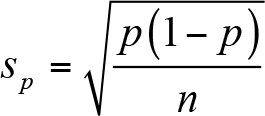
ile hesaplanır.
Ana Kütle Oranları Arasındaki Farkın ( 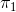 -
- 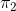 ) Aralık Tahmini: Örneklem hacminin yeterince büyük olduğu durumlarda (n1, n2>30 ) ana kütle oranları arasındaki farkın aralık tahmini,
) Aralık Tahmini: Örneklem hacminin yeterince büyük olduğu durumlarda (n1, n2>30 ) ana kütle oranları arasındaki farkın aralık tahmini,
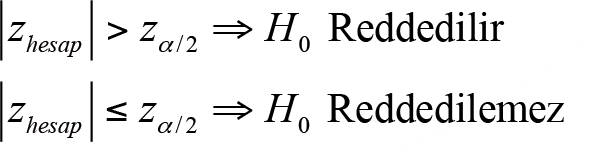
yardımıyla hesaplanır.
Hipotez Testleri
Hipotez, genel olarak belirli bir konuda ileri sürülen iddia (önerme)’dır. İstatistiksel Hipotez ise, bir araştırmada araştırma amacına uygun olarak ilgilenilen bir veya daha fazla ana kütle parametresi hakkında ileri sürülen, doğruluğu konusunda kuşku duyulan ve bundan dolayı doğruluğu (veya geçerliliği) olasılık kurallarına göre test edilme gerekliliği olan özel önermelerdir.
Sıfır Hipotezi ve Karşıt Hipotez: Ana kütle parametresinin belirli bir değere eşitliği, iki ya da daha fazla ana kütle parametresi arasında fark olmadığı biçimindeki hipotez; sıfır hipotezidir ve H 0 ile gösterilir. Buna karşın, ana kütlenin ilgilenilen parametresinin belirli bir değerden farklılığını, iki ya da daha fazla ana kütle parametresi arasında fark olduğunu ifade eden hipotez ise karşıt hipotezdir ve H 1 ile gösterilir. Bu hipotezler, ? ana kütle parametresi ve ? 0 ana kütle parametresi için iddia edilen değer olmak üzere, tek bir ana kütle parametresi için genel olarak,
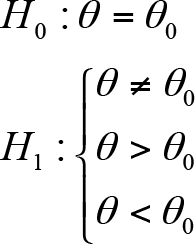
şeklinde ifade edilir.
Birinci ve İkinci Tip Hatalar
Araştırmacı araştırmanın amacına uygun olarak reddetmeye çalıştığı H0 hipotezine ilişkin belirli bir güven düzeyinde karar verdiği için varılan kararın bir hata içermesi söz konusudur ve hipotez testinde örneklem istatistiği kanıt olarak kullanıldığında karşılaşılabilecek karar durumları,
- Sıfır hipotezi gerçekte doğrudur, reddedilememiştir.
- Sıfır hipotezi gerçekte doğrudur, reddedilmiştir.
- Sıfır hipotezi gerçekte yanlıştır, reddedilememiştir.
- Sıfır hipotezi gerçekte yanlıştır, reddedilmiştir. gibi olabilir (S: 193, Tablo: 7.1). Görüldüğü üzere bu dört karardan iki tip hata yapılması söz konusudur.
I. Tip Hata: ? -Hatası olarak da adlandırılan bu tip hata gerçekte doğru olan sıfır hipotezinin reddedilmesidir. Bu hatayı işleme olasılığı ? kadardır.
II. Tip Hata: ß -Hatası olarak da adlandırılan bu tip hata gerçekte yanlış olan sıfır hipotezinin reddedilmemesidir. Bu hatayı işleme olasılığı da ß kadardır. Dolayısıyla,
? : I. tip hatayı işleme olasılığı,
ß : II. tip hatayı işleme olasılığı,
1-? : H0 gerçekte doğru olduğunda onu reddetmeme
olasılığıdır ve “ Güven Düzeyi ” olarak adlandırılır.
1- ß : H0 gerçekte yanlış olduğunda onu reddetmeolasılığıdır ve “ Testin Gücü ” olarak adlandırılır.
Hipotez Testinin Aşamaları: Hipotez testinde genel olarak izlenecek aşamalar:
- Sıfır hipotezi ve alternatif hipotezin ifade edilmesi,
- ? anlamlılık düzeyinin seçilmesi,
- Örnekleme dağılımının belirlenmesi,
- Ret bölgesinin (kritik değerin) belirlenmesi,
- Uygun test istatistiğinin hesaplanması,
- İstatistiksel kararın verilmesi
Ana Kütle Ortalamasına İlişkin Hipotez Testleri: Bu bölümde ana kütle ortalamasına ilişkin uygulamada çoğunlukla kullanılan tek ana kütle ortalamasına ve iki ana kütle ortalaması arasındaki farka ilişkin olarak gerçekleştirilen testlere değinilmiştir.
Tek Ana Kütle Ortalamasına İlişkin Hipotez Testi: Bu kısımda ilgili ana kütle aritmetik ortalaması µ ’nün belirli bir değere ( µ 0 ) eşitliği şeklinde ifade edilen sıfır hipotezinin test edilmesi işlemleri ele alınacaktır.
1. Sıfır Hipotezi ve Alternatif Hipotezin İfade Edilmesi:
Sıfır hipotezi her zaman eşitlik şeklinde ifade edilir. Alternatif hipotez ise, ana kütle ortalamasının iddia edilen değerden farlılığına ilişkin ise eşitsizlik biçiminde kurulur ve çift taraflı olduğu ifade edilir, ana kütle ortalamasının iddia edilen değerden büyük ya da küçük olduğu yönünde ise tek taraflı hipotez olarak adlandırılır.
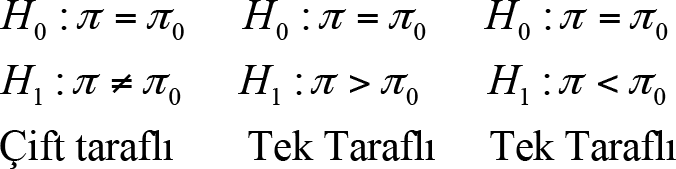
2. Anlamlılık Düzeyi ?’nın Seçilmesi: Bir hipotez testinde I. tip hatayı işleme olasılığı olan anlamlılık düzeyi genellikle 0.05 ve 0.01 olarak belirlenir.
3. Örnekleme Dağılımının Belirlenmesi: Hipotez testlerinde örneklem istatistiğinin örnekleme dağılımından yararlanılmakta olup araştırmanın amacına uygun olarak hangi örnekleme dağılımından yararlanılacağı bu aşamada belirlenir.
4. Red Bölgesinin (Kritik Değerin) Belirlenmesi: Test istatistiğinin hesaplanan değerlerinin sıfır hipotezinin reddi kararına götüreceği değerler kümesi red bölgesi olup bu bölgenin sınırında bulunan değere kritik değer adı verilir. Karşıt hipotez ana kütle ortalamasının iddia edilen değerinden büyük şeklinde ise red bölgesi dağılımın sağ ucunda olur ve büyüklüğü ? ’ya eşittir, küçük şeklinde ise red bölgesinin büyüklüğü yine ? ’ya eşit olur fakat bu kez dağılımın sol ucunda yer alır. Eğer karşıt hipotez ana kütle ortalamasının iddia edilen değerinden farklı olduğu biçiminde ise, red bölgesi dağılımın iki ucunda olmak üzere iki eşit bölgede yer alır ve büyüklüğü ? / 2 ’ye eşit olur.
5. Uygun Test İstatistiğinin Hesaplanması: Test istatistiği tek ana kütle ortalamasına ilişkin test için büyük örneklem durumunda, ana kütle varyansı bilindiğinde:
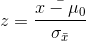
yardımıyla hesaplanır. Bu eşitlikteki 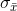
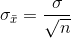
şeklinde hesaplanır. Uygulamada ana kütle varyansı genellikle bilinmediği için örneklem varyansı kullanılarak test istatistiği,
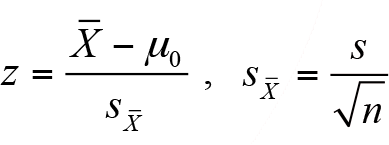
olarak hesaplanır.
6. İstatistiksel Kararın Verilmesi: Tek taraflı test için:
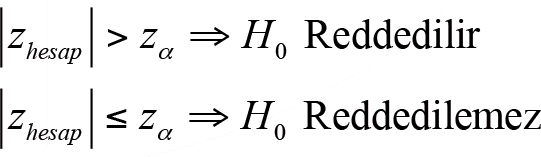
İki taraflı test için:
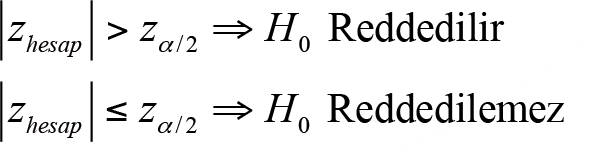
Küçük Örneklemler Durumu: Küçük örneklem durumunda Student-t dağılımına uygun olarak t test istatistiği kullanılır ve yukarıda izlenen aşamalar benzer biçimde gerçekleştirilir.

Ana Kütle Ortalamaları Arasındaki Farka İlişkin ( 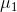 -
- 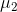 ) Hipotez Testi: Hipotezler aşağıdaki gibi kurulur:
) Hipotez Testi: Hipotezler aşağıdaki gibi kurulur:
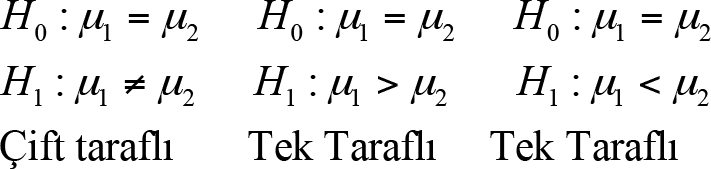
Büyük örneklem durumunda ana kütle varyansları bilindiğinde test istatistiği aşağıdaki gibidir:
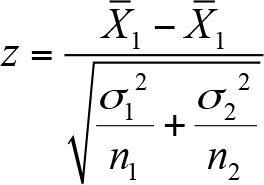
Ana kütle varyansları bilinmediğinde ise test istatistiği,
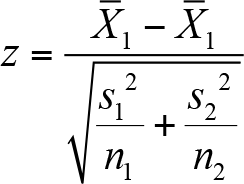
olarak hesaplanır.
Küçük Örneklemler Durumu: Küçük örneklemler durumunda kullanılacak t test istatistiği aşağıdaki gibi hesaplanır.
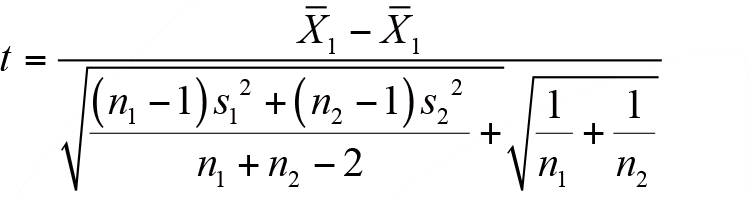
Tek Ana Kütle Oranına İlişkin Hipotez Testi: Sözü edilen test için hipotezler aşağıdaki gibi kurulur:
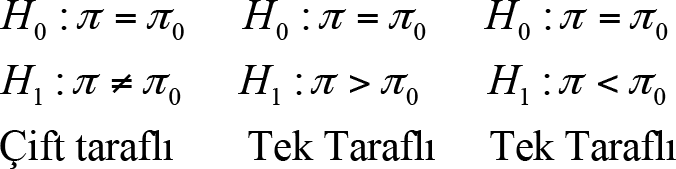
Büyük örneklem durumu için test istatistiği aşağıdaki gibi hesaplanır:
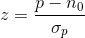
Oranın standart hatası ise, ana kütle oranı için iddia edilen değeri kullanılarak aşağıdaki gibi hesaplanır:
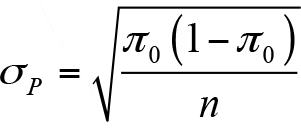
Ana Kütle Oranları Arasındaki Farka ( 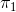 -
- 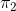 ) İlişkin Hipotez Testi: Hipotezler ve test istatistiği aşağıdaki gibi olacaktır:
) İlişkin Hipotez Testi: Hipotezler ve test istatistiği aşağıdaki gibi olacaktır:
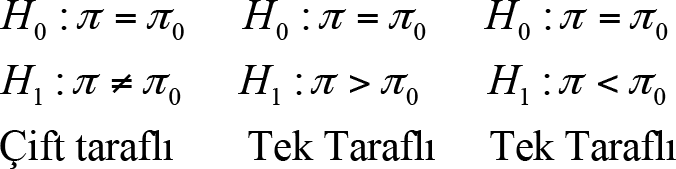

Tek-Yönlü Varyans Analizi: Tek-Yönlü Varyans Analizi, bağımlı değişken üzerinde sadece bir bağımsız değişkenin etkisinin araştırıldığı, dolayısıyla bağımsız değişkenin düzeyleri olarak ortaya çıkan gruplar arasındaki farkların istatistiksel olarak anlamlılığının araştırıldığı bir yaklaşımdır. Çözümlemede F-Testinden yararlanılır. Tek-Yönlü Varyans Analizinde, her hangi bir gözlem değerinin bileşenlerini gösteren doğrusal toplamsal model aşağıdaki gibidir:
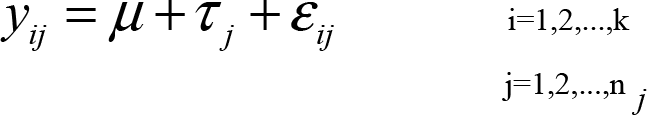
Bu modelde;
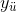 : Ana kütlenin herhangi bir terimi
: Ana kütlenin herhangi bir terimi
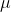 : Genel ortalama
: Genel ortalama
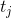 : Grup etkisi
: Grup etkisi
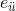 : Deneysel hatadır.
: Deneysel hatadır.
Deneysel araştırmalarda belirlenen gözlemlerin genel ortalamadan olan sapmalarının kareleri toplamını, bu sapmalara neden olan öğelere göre kısımlara ayırmak ve çözümlemek, varyans analizinin temelini oluşturmaktadır. Buna göre toplam değişim aşağıdaki gibi iki öğeye ayrılır:
Toplam Değişim=Gruplararası Değişim+ Gruplariçi Değişim (Hata)
Toplam değişim ve unsurlarını hesaplamak için,
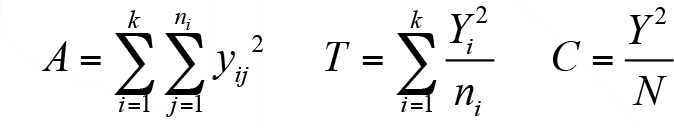
formülleri kullanılacak olup burada ij y gözlem değerlerini, Yi i’inci gruptaki gözlem değerleri toplamını, Y tüm gözlemlerin toplamını ve ni ise gruptaki gözlem değeri sayısıdır. Böylelikle kareler toplamları;
Gruplararası kareler toplamı: T-C (k-1 serbestlik dereceli) Gruplariçi kareler toplamı: A-T (N-k serbestlik dereceli) Genel kareler toplamı: A-C (N-1 serbestlik dereceli) Gruplararası kareler ortalaması 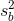 ve gruplariçi kareler ortalaması
ve gruplariçi kareler ortalaması 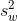 aşağıdaki gibi yazılabilir:
aşağıdaki gibi yazılabilir:
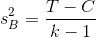
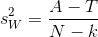
Buradan Tek-Yönlü Varyans Analizi için hipotezler:
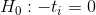 yada
yada 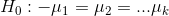
H 1 En az bir 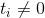 yada
yada 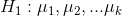 ların en az biri farklıdır.
ların en az biri farklıdır.
şeklinde olup çözümlemede kullanılacak test istatistiği,
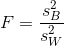
şeklindedir (S: 204, Tablo: 7.2).
şeklindedir (S: 204, Tablo: 7.2).
Ki-Kare (X 2 ) Testi: Uygulamada sayısal olmayan, başka bir ifadeyle sınıflayıcı ve sıralayıcı ölçekle ölçülmüş veri setleri ile sıkça karşılaşılmaktadır. Bu durumda sık başvurulan hipotez testi yaklaşımı X 2 testidir. Bu test, uygunluk, bağımsızlık ve homojenlik testi olmak üzere üç biçimde uygulanmaktadır. Burada önceki testlere paralel olarak Homojenlik testi açıklanacaktır.
Ki-Kare Homojenlik testinde biri örneklemlerin ait olduğu değişken (grup değişkeni), diğeri incelenen değişken olmak üzere, birinin düzeyleri satırlarda diğerinin düzeyleri de sütunlarda olacak biçimde çapraz tablo (kontenjans tablosu) olarak adlandırılan tablo oluşturulur. Bu çapraz tabloda oluşan hücrelerde ilgili birim sayısına (hücre frekansı) yer verilir.