Güç Sistemleri Analizi Dersi 5. Ünite Özet

Yatışkın-Durum İletim Hat Modelleri

Özet
Sorularla Öğrenelim

Elektrik enerjisinin, üretilen yerlerden tüketilen bölgelere aktarımı için gerekli sistemlere iletim şebekesi denir. Elektrik enerjisinin bir tüketim bölgesi içerisinde alçaltıcı trafo merkezinden alınıp tüketim bölgelerine ulaştırılması içim gerekli olan sistemlere dağıtım şebekesi denilir. Bu ünitede yatışkın durumdaki tek fazlı ve üç fazlı enerji iletim hatları incelenmiştir. İncelemede iki kapılı devre modeli kullanılmış ve modellerin karakteristik parametreleri elde edilmiştir. Kısa, orta ve uzun hatlar için bu parametreler sistemi ayrı ayrı etkilemektedir.

Kısa ve Orta Uzunluktaki Hat Benzetimleri

Göndericiden gelen gerilim akım sırasıyla VS ve IS alıcıya ulaşan gerilim ve akım sırasıyla VR ve IR olarak adlandırılırsa aradaki ilişki matris formatında aşağıdaki gibi tanımlanır.

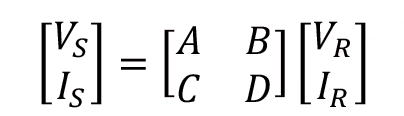
Bu matristeki A, B, C, D parametreleri R, L, C ve G sabitlerine bağlıdır. Burada A ve D parametreleri boyutsuz, B Ohm, C ise Siemens cinsindendir.

Şebekenin doğrusal, pasif ve iki yönlü iki kapılı modele uyması durumunda aşağıdaki ilişki tanımlanır.

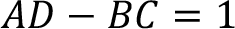
80 km’den kısa hatlar kısa uzunluklu, 80 km ile 250 km arasındaki hatlar orta uzunluklu hat olarak adlandırılır. Kısa hatlar seri direnç ve reaktansla ifade edilir, şönt admitans ihmal edilir. Üç fazlı devrelerde Z empedansı R ve L parametrelerine bağlı olarak ilk önce birim uzunluk için hesaplanır. Birim uzunluğa düşen empedans hat uzunluğuna çarpılarak toplam hat empedansı bulunur. Benzer şekilde Y şönt admitansı G ve C parametrelerine bağlı olarak yine birim uzunluk için hesaplanır. Hat uzunluğuyla çarpılarak toplam şönt admitansı bulunur.

G şönt iletkenliği havadan gerçekleştirilen iletimlerde ihmal edilir. Bu durumda KGK ve KAK eşitliklerine göre A ve D parametreleri 1, B parametresi toplam empedans değeri C parametresi ise 0 olarak ele alınır.

Orta uzunluklu hatlarda, toplam şönt kapasıtans değeri hattın her iki ucuna eşit dağıtılır. Nominal ? devresiyle modellenen bir orta uzunlukla hat KGK denklemiyle modellenir ve A, B, C ve D parametreleri aşağıdaki gibi bulunur.

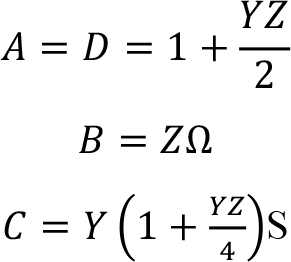
A,B,C,D parametreleri hattaki yüklenme ile birlikte hat voltajındaki değişikliklerin ifade edilmesi için kullanılır. Yüklenme: Uçlara bağlanan yükün elektriksel olarak artması veya azalması durumudur.

Gerilim Regülasyonu: Gönderici uçtaki gerilimin sabit tutulması durumunda alıcı-uç tarafında bulunan yükün, yüksüz durumdan tam-yük durumuna geçerken alıcı-uçta gerçekleşen gerilim değişimidir. Aşağıdaki denklem ile tanımlanır.

VR yüzde olarak gerilim regülasyonunu, | V _RNL | Yüksüz durumdaki alıcı uç tarafının gerilim büyüklüğünü, | V _RFL | tam yük durumundaki alıcı-uç tarafındaki gerilim büyüklüğünü gösterir. Yüksüz durumda I _RNL = 0 ve V _S = V _RNL olarak hesaplanır.

Uygulamada iletim hattı nominal değerden daha fazla yüklendiğinde hat gerilimi düşer, daha düşük yüklendiğinde hat gerilimi yükselir. Çok yüksek gerilim hatlarında gerilimdeki % ±5’lik bir değişim, %10’luk bir gerilim regülasyonuna denk gelir. Alçak gerilim hatlarında %10’luk bir gerilim regülasyonu iyiye yakın çalışma koşulları olarak adlandırılır.

Hattın yüklenebilirlik durumu termal limit, gerilim-düşüm limiti ve yatışkın durum kararlılık limiti ile sınırlandırılmıştır. Termal limit iletken malzemenin maksimum sıcaklığı ile belirlenir ve bu sıcaklık iletken üzerinden geçen akıma ve akımın geçiş zamanına, ortam sıcaklığına, rüzgar hızına ve iletken yüzeyindeki şartlara bağlıdır.

Kısa hatlar için yüklenebilirlik iletkenin termal limiti devre kesicilerin anma değerlerine bağlıyken, orta uzunluklu hatlarda gerilim-düşüm limitine bağlıdır.

V _R \ V _S ? 0,95 olan hatlarda güvenli çalışma şartlarının sağlandığı kabul edilir.

İletim Hatlarına Ait Diferansiyel Denklemler

Gerilimin hat uzunluğuna bağlı türevi; birim uzunluğu düşen empedans çarpı akımı verir. Aynı şekilde akımın hat uzunluğuna bağlı türevi birim uzunluğa düşen şönt admitansı çarpı gerilimi verir. Gerilimin ikinci dereceden türevi ise birim uzunluğa düşen empedansın, birim uzunluğa düşen admitansın ve gerilimin kendisinin çarpımına eşit olur. Elde edilen homojen diferansiyel denklemin çözümü aşağıdaki gibidir.

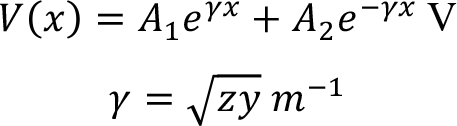
Burada A ₁ ve A ₂ integrasyonu sabiti, 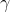$\gamma$ yayılım sabiti olarak adlandırılır. Ayrıca diferansiyel denklemin devamında Z _c karakteristik empedansına aşağıdaki gibi ulaşılır.

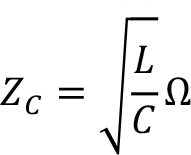
Ayrıca konuma bağlı gerilim ve akım değerleri aşağıdaki gibi ifade edilir.

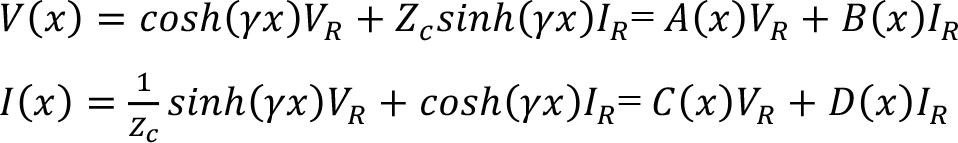
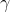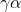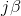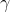
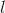
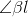Gerilim ve akımın alıcıya ulaştığındaki değerleri yukarıdaki denklemlerde x=l alınarak hesaplanabilir. Yayılım sabiti $\gamma$ = $\gamma \alpha$ + $j \beta$ m ^-1 şeklinde alınırsa e = e ^a $\angle \beta\l$ olarak hesaplanır.

Eşdeğer ? Devresi

Eşdeğer ? devresiyle ifade edilen iletim hattı için A, B, C, D parametreleri aşağıdaki gibi ifade edilir.

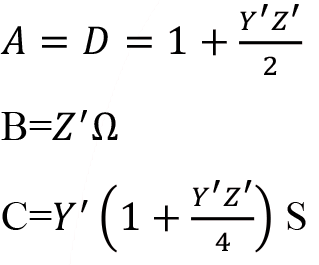şeklinde bulunur.

Burada Z ¹ = Z x F ₁ ve Y ¹ = Y × F ₂ ’dir.

F ₁ ve F ₂ düzeltme katsayıları aşağıdaki gibi ifade edilir.

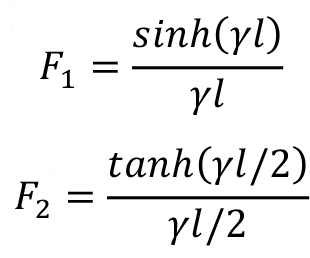
Kayıpsız İletim Hatları

Kayıpsız kabul edilen bir hat için gerçel direnç ve gerçel iletkenlik 0 kabul edilir. Bu durumda empedans sadece bobin(L) değerine admitans kondansatör(C) değerine bağlı tanımlanır. Bu durumda karakteristik empedans Zc aşağıdaki gibi bulunur.

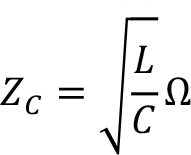
Bu karakteristik empedans aynı zamanda dalga empedansı olarak da adlandırılır.

Dalga boyu; gerilim veya akım fazını, 3600 periyodunda değiştirmesi için gerekli olan uzaklık olarak tanımlanır.

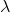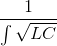$\lambda$ = m şeklinde bulunur. Buradaki 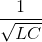$\frac{1}{\sqrt{LC}}$ ifadesi gerilim ve akımın hat boyunca yayılım hızını verir.

Dalga Empedans Yüklenmesi(SIL) : Kayıpsız hat aracılığıyla dalga empedansına eşit değerdeki bir yük direncine iletilen güç değeridir. SIL durumunda gerilim profili yataydır yanı hat boyunca gerilim değeri sabittir. Herhangi bir andaki güç değeri ise aşağıdaki gibi ifade edilir.

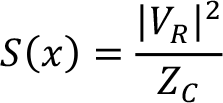
Bir iletim hattı için gerilim profilleri;,

Yüksüz durum,
SIL durumu,
Kısa-devre durumu,
Tam-yük durumu

Olarak sıralanabilir.

Yatışkın durum kararlılık limiti;

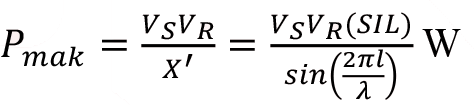
ile ifade edilir. Bu değer aşıldığında gönderici uçla alıcı uç arasındaki senkronizasyon kaybedilir ve tehlikeli sonuçlar ortaya çıkabilir.

Maksimum Güç Akışı

Teorik anlamda iletilen maksimum gerçek güç veya yatışkın durum kararlılık limiti aşağıdaki gibi belirtilir.

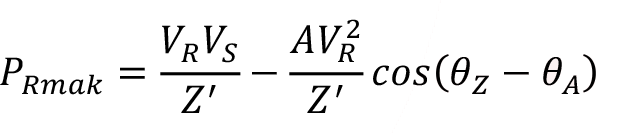
Hat gerilimlerini nominal değerde tutmak için endüktör ve kapasitör devre elemanları kullanılır. Şönt endüktanslar yüksek gerilim hattı boyunca seçilen noktalarda herbir faz ile toprak arasına konulurlar. Şönt reaktörlere ilaveten şönt kondansatörler de reaktif güç vermek için kullanılabilir. Ayrıca statik VAR sistemleri olarak tristörlü sistemler de kullanılabilir. Bu sistemler tristör anahtarlamalı kapasitörler, tristör anahtarlamalı endüktörler ve paralel kapasiteli tristör anahtarlamalı endüktörler olarak gruplanabilir. Statik VAR sistemlerinin en büyük üstünlüğü; ani yük değişimlerinde çok hızlı cevap verebilmeleridir. En büyük dezavantajı ise harmonik adı verilen parazitleri üretmeleridir. Seri kapasitörler uzun hatlarda hattın yüklenebilirliğini arttırmak için de kullanılabilir. Nominal gerilim; motor, lamba, ısıtıcı gibi cihazların en verimli çalıştığı gerilimdir. Bu değer aşıldığı zaman cihazlarda arızalar oluşabilir veya verimsiz bir çalışma ortamı oluşur. Gerilimi nominal değerde tutmak için üretim yapılan merkezde değil, güç ileten iletim şebekelerinde ayarlamalar yapılır. Dağıtım şebekesinde gerilim sabit tutulmaya çalışılırken, iletim şebekesinde belirli bir tolerans payı bırakılır.